Medium and long infrared waves possess many distinct and useful characteristics，such as penetrating tissue，fog and smog，radiation emitting from objects related to temperature and material，which enables imaging and identifying the targets through scattering media even in the dark. These outstanding characteristics of infrared imaging make it widely used in environmental monitoring，biomedical diagnosis，military reconnaissance and so on. However，the cost of megapixel sensors in the infrared imaging is expensive，especially for high-performance cooled detectors，often extending tens of thousands of dollars. As a result，despite the dramatic utilization potentially，the high spatial-temporal resolution and online monitoring cameras are beyond the reach of many engineers and researchers.

Compressed sensing（CS）^［1-3］，as a distinctive sampling theorem，is an excellent information collection scheme with a rate less than that required for the traditional Nyquist–Shannon sampling while ensuring accurate reconstruction. The single pixel camera（SPC）^［4］ is a typical application of CS in the field of compressive imaging，which has several advantages such as expanding pixels and low cost. At present，SPC is applied to the fields of spectral imaging，three-dimensional imaging，microscopy，etc. However，CS has several limitations such as high time cost and low image quality since it involves a series of sequential measurements. The focal plane array（FPA）^［5］ sensors composed of parallel multi-SPCs enable parallel sampling and effectively improve the acquisition speed and imaging quality^［6］. This type of compressive imaging（CI）is a relatively new development，and it provides an effective way to use low-cost and low-resolution infrared sensors to achieve high-resolution infrared images. Recently，research on parallel CI has focused on improving imaging quality^［7-10］，modulation solutions^{［7，11-14］}，optical path correction，etc.，and has been applied to near-infrared and mid-infrared imaging^{［5，15，16］}. Increasing the imaging speed to achieve real-time high-resolution monitoring for the infrared CI is an important goal of this research，and there is currently a lack of relevant research.

Thus far，two limiting factors of imaging speed in parallel CI are mainly known：the optical modulation speed and image reconstruction efficiency.

（1）In the optical modulation phase，CI usually employs a binary random matrix or an orthogonal matrix. A digital micromirror device（DMD），which enables high-speed spatial light modulation（SLM），is widely used in optical modulation. However，DMD only provides binary modulation. When the DMD loads a gray pattern from a modulation matrix，such as random Gaussian or random partial Fourier，Discrete Fourier Transform（DCT）or Fast Fourier Transform（FFT），each frame has to be obtained with time-sharing pulse width modulation that results the increment of the modulation time exponentially and goes against high-speed imaging. Although the DMD can provide a frame rate up to 20 kHz，the modulation frequency of an 8-bit gray pattern is about 250 Hz^［17］. Hence，the modulation time of gray pattern increases，which is unsuitable for high-speed imaging.

A +1/-1 Hadamard matrix is one of the few choices for fast sampling and is easy to implement. Therefore，using the +1/-1 or Hadamard matrix for CS modulation can reduce the number of measurements and increase the imaging speed in the acquisition phase.

（2）In the recovery phase，the CS reconstruction algorithm involves intensive computation iterations and is suitable for parallel processing. Meanwhile，asynchronous parallel processing is also suitable for sequential sampling and iterative reconstruction to reduce the processing time.

Both the +1/-1 Hadamard modulation and CS parallel processing are considered to increase imaging speed. In addition，in order to increase imaging speed，parallel MBCS imaging with GPU acceleration is proposed. MBCS combines the multiple blocks of observations into a merged block for reconstruction，which benefits from preserving the edge information and continuity information among the blocks and reduces the blocking effect of traditional block CS. Also，the number of blocks is reduced by combining blocks，which eliminates some small block initializations that appear in the traditional block CS，thereby，reducing the reconstruction costs.

The main tasks in this work are as follows：Firstly，for the modulation，the image performance of +1/-1 Hadamard matrix is applied for fast imaging. Secondly，for the reconstruction process，the proposed MBCS can effectively improve the image recovery speed and ensure recovered image quality since the combined blocks retain edge information. We found that +1/-1 matrix showed a good performance with under-sampling and the image reconstruction performance was related to the block size. Different under-sampling ratio reconstruction procedures show the same law that the peak signal-to-noise ratio（PSNR）increases first and then decreases as the block size increases，while the reconstruction time decreases first and then increases. There exists an optimal block size for achieving good reconstruction quality and speed. Furthermore，we designed a（multi-frame）GPU-based algorithm to increase the iteration speed. We experimentally demonstrated that the parallel MBCS imaging with GPU acceleration could achieve fast sampling and reconstruction，thereby promoting high-speed，real-time，large-array imaging.

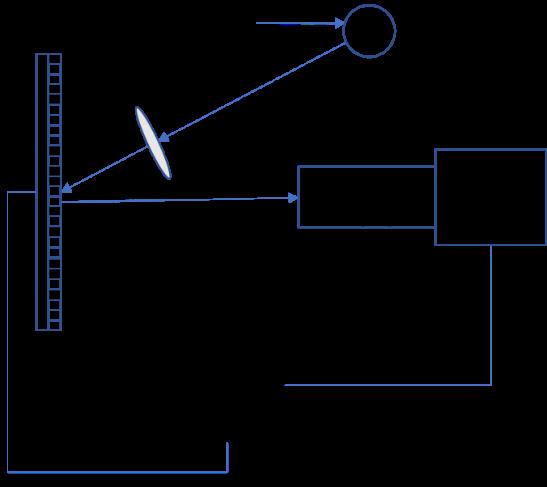
In this section，we will describe parallel optical FPA，two-cascade imaging，and GPU-adaptive reconstruction architecture. In the low-resolution image acquisition phase and high-resolution image estimation phase，the light reflected by an object is imaged by an objective lens and modulated on the DMD，and then reimaged on the detector FPAs by a projection image lens；finally，the high-resolution image is recovered from the acquired low-resolution image by real-time parallel programming on the GPU.

In this section，we describe the BCS imaging architecture shown in Fig. 1，which includes parallel FPA，two-cascade imaging，and GPU-adaptive reconstruction system. The optical system completes the imaging process via two-cascade imaging. Firstly，the lamp illuminates the object，and the light reflected（or transmitted）by the object is imaged on an SLM. The SLM is configured synchronously by a host computer to impart distinct high-resolution intensity modulation onto the object field for each projection. Secondly，the reflected light from the SLM is reimaged onto the detector array through the image lens. Finally，the high-resolution image is recovered from the acquired low-resolution images by real-time parallel programming on the GPU.

In the experimental optical setup，the light source was a View Solutions halogen lamp. We utilized a Texas Instruments digital micromirror device（TI DMD）as the SLM. The DMD contained 1024 × 768 micromirrors，each mirror of size 13.68 × 13.68 µm. Each mirror could be independently rotated to either +12° or -12° position. We used an objective lens with a focal length of 50 mm to focus the light onto the DMD. We used a 1388 × 1038 sensor（ALLIED Vision Technologies Manta G-145）with a pixel size of 6.45 × 6.45 µm connected to an image lens with a focal length of 30 mm to validate the proposed method，which is the same to procedures in the medium and long infrared wave spectrum. The sensor and image lens faced the DMD and could be rotated around the optical axis，so as to align the relative position of the sensor and DMD as accurately as possible.

In this paper，the compression ratio scale of C×C denotes pixels number ratio of high-resolution scene to low-resolution image，while the sampling rate is the ratio of the modulation times to the number of the pixels. In the optical system，compression ratio scale of C×C means that the projection refers to C×C pixels on the DMD mapping to one pixel on the detector. In our actual experiment，the effective regions of the DMD and sensor were 512 × 512 pixels and 1024 × 1024 pixels，respectively. Quantitatively，each micromirror on the DMD corresponds to 2 × 2 pixels of the sensor. Further considering of the difficulty of mapping a mirror element of DMD to a detector pixel accurately and proportionally，we took into account the fact that DMD mirrors may reflect light to not only the target detector pixel，but also reflect light to the neighboring pixels. To minimize image registration error and improve image recovery quality in practice，for all the experiments，we used 4 × 4 binning of the DMD mirrors to generate an effective mask element with 54.72 × 54.75 µm. Correspondingly，for three compression ratio scenarios such as 2 × 2，4 × 4 and 8 × 8 in the following experiment，respectively，16 × 16，32 × 32 and 64 × 64 detector pixels on the sensor were merged into an elementary super pixel.

In an SPC，the observation value vectors of all pixel intensities Y are linear combinations of image signals X with added noiseE，with the coefficient assigned by modulation functionΦ. The equation can be represented in matrix-vector means as follows：

The FPA functions parallel to the measuring image system，which employs a focal plane array detector instead of the single pixel detector of the SPC via image plane coding and provides a flexible optical architecture and multiplex simultaneous information acquisition method using FPA pixels measurement of the inner product of modulation function multiplied with the image. Consequently，the original image is compressed and recorded on the low-resolution sensor. The compression ratio is equal to the mapping of the signal from mask elements to a single pixel element of sensor by C×C∶1，which is customized depending on system-specific requirements and configuration. Thus，the whole N×N scene image is divided into several blocks of size C×C，and parallelly imaged onto N/C×N/C pixels in a two-dimensional detector array instead of as a single pixel. Each detector acts as a photodiode in the SPC，and the model is expressed as

where X(i) denotes the i-th block of the scene image in column-wise way；Y(i)is the i-th observed vector column-wisely acquired on the sensor；Φ(i) is the projection operator of i-th block sub-scene-image.

Let x∈ℝB×B be one of the blocks consisting of the scene image formed on the DMD，and let ϕ,ϕ*∈ℝB×B be complementary measurement binary patterns displayed on the DMD. For the experiment in this study，we used each row of the Hadamard matrix as the patterns. Then，y,y*∈ℝBC×BC were the complementary measurements obtained at the sensor，and Δy∈ℝBC×BC was the complementary differential measurement vector. Each measurement obtained at the sensor can be represented as follows：

Eventually，one measurement of the complementary matrices is given as

where ⊗ denotes the element-wise product，and e1and e2 are the added noise. In this way，the measurement matrix is changed from the 0-1 binary matrix to the +1/-1 binary matrix with mean of zero to satisfy the RIP criterion，which is a necessary condition for accurate reconstruction of CS.

The use of an orthogonal gray matrix results in a long sampling time，and fails to obtain images fast. Although a relatively high reconstruction speed can be achieved by inverse transformation，the full sampling is inevitable；otherwise，the quality of under-sampling will be very poor or the full sampling will increase the sampling time. In the proposed optical architecture，DMD functions as the SLM to achieve 0/1 modulation on the gray image. The advantage of the +1/-1 Hadamard matrix is that it is easy to realize and provides notable imaging speed；hence，the Hadamard matrix was chosen as the modulating function Φ. Owing to the orthogonal properties of the Hadamard matrix，an inverse operation on the full sampling value could directly provide the reconstructed image. However，full sampling requires more time for imaging，and inverse operation on under-sampling does not provide a good result. The comparison between pseudoinverse operation by ϕTϕϕT-1 and CS reconstruction with random under-sampling was simulated for sizes of 32 × 32，64 × 64，and 128 × 128 pixels. The subsampling rate was 0.3，and the measurement times were 307 for 32 × 32 pixels，1229 for 64 × 64 pixels，and 4915 for 128 × 128 pixels. The measurement times，PSNR and feature similarity indexes（FSIM）^［18］ of the reconstructed images using the phase congruency（PC）and the gradient magnitude（GM），defined in Eq.（6），are indicated in Fig. 2. The results show that CS achieves more excellent reconstruction performance than an inverse operation with +1/-1 modulation matrix using under-sampling. Both metrics of the PSNR and FSIM of CS were obviously better than inverse operation for different resolutions.

where x represents position in the image，PCmΧ=maxPC1Χ,PC2Χ is the maximal phase congruency（PC）value at the position x between the two images，SLΧ is calculated from the combined similarity of PC and GM.

Also，to evaluate the reconstruction accuracy of the proposed method，the PSNR between the original and reconstructed images was adopted as a performance indicator：

where x and x^ denote the original and reconstructed images，respectively，and ∙2 denotes 2-norm.

This section describes the construction method of the measurement matrix and projection vector for a configurable compression ratio scale of C×C. We first introduce the measurement matrix and projection vector B×B multiblocks combination for CS（MBCS）reconstruction. In addition，the inverse operation reconstruction will not be applicable for constructing a new measurement matrix because multiblocks may not have Hadamard’s orthogonal property. Fig. 3 depicts a case of construction of a measurement matrix for a compression ratio of 4 × 4（4 × 4 pixels as one element block），and multiblocks of 2 × 2（8 × 8 pixels as one combined block）corresponding to four measurements for each combined element block.

First，the image is divided into several element blocks B×B（consisting of integral multiple of C×C base blocks）of identical sizes，and each block is a parallel SPC reconstruction block. Second，each parallel SPC coding block mask（C×C）on the SLM is generated from a different row of the Hadamard matrix（C2×C2），and complementary positive–negative measurements are implemented to improve the CS imaging quality. Moreover，the parallel SPC block mask is programmable，and block size can be configured depending on the system-specific requirements. Third，a unit of projection vectors（B×BC×C×B×B）from the multi-SPC blocks occurs successively in block-wise and column-wise manner to ensure the GPU computer cores（GPU CCs）work at full capacity owing to a single instruction，multiple data（SIMD）parallelism scheme. The maximum number of all units is C×C，while the number of measurements is an integral multiple of the unit of projection vectors. Finally，several units of projection vectors derived from the Hadamard matrix are merged to form the whole measurement matrix.

The observed value vectors of all partitioned blocks are synchronized with each projection vector in the well-designed measurement matrix. First，the parallel blocks in the observed results are successively arranged in a column-wise manner. Second，column vector of the observed value for each block originates from the corresponding linear combination of blocks in the measurement sequence. Therefore，each low-resolution image consists of the projection results of all element blocks，while the observed vector in each block consists of the observed values of specific blocks distributed over the corresponding position of every low-resolution image. The measurement matrix is depicted schematically in Fig. 4.

We simulated the under-sampling imaging process with the image size of 128 × 128 pixels. The compression rate was 8 × 8，and the under-sampling rates were 0.8125，0.6875 and 0.5. The construction of the measurement matrix and the observed values for different block sizes refer to the method described in section 1.4.

Fig. 5 shows the PSNR and recovering time with different block sizes and different under-sampling rates of 0.8125，0.6875 and 0.5. We found that there was an optimal recover-used block size to achieve the best reconstruction quality for all the under-sampling rates；meanwhile，a high-resolution image was reconstructed with the highest speed. The different under-sampling ratio reconstruction procedure shows the same regularity that the PSNR increases first and then decreases with the block size. In contrast，the reconstruction time decreases first and then increases with the block size. As the block size increases，the reconstruction gradually becomes faster and then slows down，while the reconstruction quality gradually improves；however，beyond a certain block size，the quality does not improve anymore.

The MBCS reconstruction results are expected to be better than those of single-block reconstruction，which is the case of a block size of 1. This is because multi-blocks reconstruction is expected to preserve more edge information and continuity information between the blocks comparing with a single block；furthermore，MBCS improves the overall sparsity of the measurement matrix. In addition，when the overall reconstruction is divided into many small parts to be rebuilt separately，more time is spent on variables and algorithm initialization. Initially，as the block size of the reconstruction increases，the speed increases. Later，as the size increases further，the computational cost of each block reconstruction increases rapidly，and the overall reconstruction time starts increasing. These regularities motivate the design of block-compressive sensing reconstruction.

The GPU is a computing device capable of executing many identical programs simultaneously and processing different data with a large number of threads in parallel^［19］. Hence，it is appropriate for computing intensive calculation relay on the characteristic framework and schema known as the SIMD or data parallelism. NVIDIA introduced a parallel developing platform to facilitate programming on the GPU. This platform is called the Compute Unified Device Architecture（CUDA）^［20］. It makes the system more flexible and transplantable. Additionally，the CUDA programming model uses an SIMD strategy to efficiently use the GPU computational hardware and memory bandwidth. The GPU and CPU collaborate in the form of the kernel function and the host in the CUDA program，respectively.

The CS reconstruction procedure can be improved using the high-performance computing characteristics of the GPU and parallel image acquisition on FPA. According to related research results，the traditional CS reconstruction algorithm（for instance，Total Variation，TV）spends time mainly on matrix operations in each iteration of TV optimization，such as linear and multiplication operations. This seriously affects the performance. Hence，the GPU can be used to reduce time cost and improve recovery speed drastically. In addition，it is important to minimize the data transmission overhead cost between the host and device. To efficiently exploit and utilize the performance of the GPU for matrix manipulation，several strategies were proposed：（a）Implementing sparse matrix multiplication and sparse matrix-vector multiplication based on cuSparse library to accelerate procedure；（b）Storing and loading the matrix in a sparse format used for sparse matrix multiplication operation，which can effectively improve GPU performance；（c）When rebuilding blocks sequentially，avoiding reloading the measurement matrix into the GPU global memory from an external storage，and using a consistent measurement matrix derived from the same patterns for each block；（d）Alternating the measurement matrix size derived from the FPA coding scale and the optimal partitioning block size described in the previous sections depending on the problem size and equipment characteristics（such as scene size and computer performance）；and（e）Merging several frames together into one frame to reconstruct.

Fig. 6 shows the blocked compressive sensing reconstruction procedure with GPU acceleration. Suppose the DMD has a resolution of N×N micromirrors，and the sensor has NC×NC pixels such that each pixel maps to C×C size of micromirrors on DMD. Then，the image will be recovered from m(m≤C×C) times measurements with B × B block size. The procedure is as follows：

（1）Prepare a blocked projection matrix on the GPU referring to the method described in section 1.4. Generate a full blocking projection matrix with dimensions (C×C)×(B×BC×C×B×B) and undersampling blocking projection matrix of size m×(B×BC×C×B×B)，and then convert it into CUDA sparse matrix format.

（2）Prepare the block observed values on GPU by the method described in section 1.4. To achieve a higher reconstruction efficiency，corresponding low-resolution observed values should be loaded into the host，and multiframes should be merged into one frame N×N. The next step consists of differentiating the observed values from the positive–negative complement measured images，and dividing each frame into N×NB×B blocks and reshaping each frame into B×BC×C×1 in column-wise.

（3）Reconstruct each block with the acceleration GPU functions and stitch all reconstructed high-resolution blocks into a high-resolution overall frame. In this step，the matrix structure definitions in the Compressed Sparse Column format on CUDA device and host and GPU kernel functions related to linear operation and matrix-vector multiplication are used.

The experiment optical setup described in section 1.2 is the optical prototype architecture. The reconstruction system is equipped with Intel Core i7-9700K 3.60 GHz ×8，GeForce RTX 2080Ti（4352 computational cores；clock frequencies are 1350–1635 MHz；11 GB GDDR；352 bit bandwidth；access rate is 14 GB/s；and throughout rate is 616 GB/s）. The operating system is Ubuntu 18.04.2 LTS 64 bit. The object scenes of the experiment are as follows：（a）A digital chart^［21-22］ called the virtual resolution board present on the DMD；（b）A black-and-white film with Chinese characters printed with “Chinese Academy Science” in Chinese as the transmitting object；（c）The eye of a toy as a reflective object. Each object scene had 128 × 128 pixels. The resolutions of the sampled images were 64 × 64，32 × 32，and 16 × 16 pixels.

According to the experimental reconstruction results，high-resolution imaging can be achieved with low-cost and low-resolution sensors. Furthermore，sampling data transmission only needs very low bandwidth，and this helps to improve the frame rate of high-resolution imaging.

Fig. 7 and Table 1 show the image acquisition examples using the optical system mentioned above and the reconstruction results by MBCS and traditional block CS. The measurement times are as follows：for 64 × 64 low-resolution sampling，the time is 12 288；for 32 × 32 sampling，it is 11 264；and for 16 × 16 low-resolution sampling，it is 10 240. The left side of the figure shows the captured low-resolution images with different compression ratios^［12］ of 2 × 2，4 × 4，and 8 × 8，with sizes of 64 × 64，32 × 32，and 16 × 16 pixels，respectively. The middle side of the figure shows the corresponding 128 × 128 pixels high-resolution images with proposed MBCS. The right side of the figure shows the results with the traditional Block CS. The low-resolution images’ detail in the figure is severely blurred. With a 4 × 4 or 8 × 8 compression ratio，the low-resolution images of the digital chart（a-2 and a-3）are indistinguishable，and the low-resolution images of characters on the film（b-2 and b-3）are unrecognizable，and the texture of the grayscale images（c-2 and c-3）is noticeably worsened. In comparison，in the bright stripes containing 1 pixel，2 pixels，4 pixels，and 8 pixels in the digital chart，and the characters on the film were recovered accurately and could be distinguished；also，the texture of eye in the recovered image “TOY” was vivid. For the high-resolution images recovered by traditional Block CS and the proposed MBCS，the qualities of the former results are lower than the latter. For example，in the case of 2×2 compression ratio depicted in a-7）b-7）and c-7），the traditional Block CS failed to reconstruct in some small blocks；and in a-8）b-8）c-8）a-9）b-9）and c-9），the block boundary effect was more obvious in the former. Quantitatively，the PSNR and the FSIM of the experiment results showed that MBCS results were better than the traditional block CS.

We compared the reconstruction time implemented on the GPU with the reconstruction algorithm implementation on the CPU. We performed a simulation to recover 32 × 32，64 × 64，and 128 × 128 pixel head phantoms^［23］ in Matlab with random measurements and the same subsample ratio of 0.3 on the GPU. The results of the reconstruction time and acceleration ratio are listed in Table 2. The results show that the reconstruction algorithm with GPU acceleration has strong advantages in terms of computation speed，and the reconstruction time tends to decrease as the image becomes larger. As the image size increases，the time for both reconstruction algorithm increases，the speedup ratio of GPU algorithm and CPU algorithm increases more. This shows that the GPU algorithm can improve the reconstruction speed very well，and the effect is more significant when processing large-scale images. Although both the CPU reconstruction algorithm and the GPU acceleration increase the computational complexity as the image becomes larger，GPUs have the advantages of more parallel computational cores than the CPUs to process more pixels simultaneously. Therefore，in this simulation experiment，the execution time of the CS reconstruction algorithm with GPU acceleration changes smoothly as the image size increases.

Then，the MBCS reconstruction algorithm with GPU acceleration was applied to the experimentally acquired images from the optical architecture described herein. The results show the outstanding performance of the MBCS algorithm on GPU. A larger block has more efficient reconstruction performance，thereby verifying the effectiveness of the GPU acceleration strategy described in section 1.5.

In the experiment，first，we attempted to reconstruct the high-resolution image with a size of 128 × 128 pixels from the acquired low-resolution images with a size of 64 × 64 pixels at a compression ratio of 2 × 2. Then，multiple 64 × 64 pixels low-resolution images were manually stitched into 128 × 128 pixels and 256 × 256 pixels by using 4 and 16 low-resolution images to reconstruct high-resolution images of sizes 256 × 256 and 512 × 512 pixels，respectively. Thus，multiple captured low-resolution frames can be stitched into a new large one. That is equivalent to reconstructing multiple images rapidly and simultaneously to further increase the frame frequency of reconstruction.

Table 3 lists the performance of the MBCS algorithm with GPU acceleration. The results show that this performance is much better than that of the CPU reconstruction algorithm for a block size greater than 16 × 16.

First，the experiment results shown in Fig. 8，Fig. 9，and Fig. 10 are consistent with the simulation experimental results as the size of the measurement block increases. For the CPU reconstruction process，as the block size initially increases，the reconstruction time decreases. Later，when the size is further increased，the computational cost of block reconstruction increases rapidly，and the overall reconstruction time increases，too. This phenomenon is consistent with the simulated results obtained using CPU MBCS algorithm as shown in Fig. 5. However，for the GPU acceleration process，the overall reconstruction time decreases depending on the number of GPU computational cores and other hardware quality. Because GPU acceleration process involves data transfer between CPU host and GPU device and the experimental results consider the actual overall reconstruction time，the small block size would cause relatively more extra data transfer expenditure and the reconstruction time of CPU algorithm may be smaller than GPU algorithm in this situation. These trends are also shown in Fig. 8，Fig. 9，and Fig. 10. The MBCS algorithm with GPU acceleration completes high-resolution image reconstruction faster when the block size is greater than 16 × 16. Even the average acceleration ratio can reach hundreds of times when the block size is greater than 64 × 64 as shown in the column of “GPU（s）” in Table 2.

Second，the average time for single-block reconstruction with different image sizes using the MBCS algorithm with GPU acceleration is very close in the experiment according to the data in “AVG/blk（s/blk）” column in Table 2. This result suggests that reconstruction with a bigger block should be more reasonable under the given hardware configuration. A comparison of the reconstruction speeds among 128 × 128，256 × 256，and 512 × 512 pixels shows that multi-image stitching is feasible. From the data in the last row of Table 2，the MBCS algorithm with GPU acceleration used a block size of 256 × 256 to reconstruct one 512 × 512 high-resolution image in about 0.2 s，which is equivalent to reconstructing 4 256 × 256 high-resolution images or 16 128 × 128 high-resolution images in 0.2 s. For the 128 × 128 scene，the recovery speed of stitching multiple frames can reach 0.013 seconds per frame；in other words，the high-resolution frame rates can achieve real-time or near-real-time performance. However，construction of the measurement matrix is too difficult when the image size is too large. Hence，the MBCS reconstruction algorithm with GPU acceleration can use frame-stitching to improve the reconstruction frame rate and large block reconstruction to obtain high-quality reconstruction images.

We proposed an optical parallel image prototype system based on the FPA CI system combined with the MBCS algorithm，which can be used low-cost and low-resolution infrared sensors to perform real-time imaging and display of short and medium infrared spectrum. And through theoretical analysis and the visible optical imaging experiments，the effectiveness and practicability of the proposed MBCS method were verified. We also discussed the MBCS measurement matrix of the reconstruction model and under-sampling feature of CS for fast imaging in the highly parallel CI system. The reconstruction performances related to the block size，merging multi-images into a single image and MBCS reconstruction strategy with GPU acceleration were analyzed. In the experiment，we used the Hadamard matrix entries as the modulation pattern for parallel image acquisition and successfully achieved high-resolution scene imaging using a low-resolution sensor. It proved that the MBCS can effectively improve the reconstructed image quality greater than the traditional method，meanwhile there is an optimal block size to achieve fast reconstructing and high imaging quality. Depending on the GPU-based prototype and architecture，both the low-resolution image acquisition and high-resolution image reconstruction were achieved simultaneously in real-time.

In the optical experiment，the maximum compression ratio 8×8 was carried out. The imaging resolution can be increased by 64 times，but it is not the upper limit. The system can well solve the inadequate resolution problem of the detector in infrared imaging，or even THz and other fields. The frame performance of 5Hz can satisfy the requirements of a great many fast imaging scenes. In future work，we will explore more optimization strategies，such as the use of multiple GPU devices，and try more efficient modulation matrix and reconstruction algorithms to reduce data transfer expenditure between the CPU host and the GPU device. We are also studying three-dimensional imaging and an embedded arm signal processors with a high-performance architecture.