Fast and robust phase retrieval for masked coherent diffractive imaging

Li Song; Edmund Y. Lam

doi:10.1364/PRJ.447862

Abstract

Conventional phase retrieval algorithms for coherent diffractive imaging (CDI) require many iterations to deliver reasonable results, even using a known mask as a strong constraint in the imaging setup, an approach known as masked CDI. This paper proposes a fast and robust phase retrieval method for masked CDI based on the alternating direction method of multipliers (ADMM). We propose a plug-and-play ADMM to incorporate the prior knowledge of the mask, but note that commonly used denoisers are not suitable as regularizers for complex-valued latent images directly. Therefore, we develop a regularizer based on the structure tensor and Harris corner detector. Compared with conventional phase retrieval methods, our technique can achieve comparable reconstruction results with less time for the masked CDI. Moreover, validation experiments on real in situ CDI data for both intensity and phase objects show that our approach is more than 100 times faster than the baseline method to reconstruct one complex-valued image, making it possible to be used in challenging situations, such as imaging dynamic objects. Furthermore, phase retrieval results for single diffraction patterns show the robustness of the proposed ADMM.

1. INTRODUCTION

It is possible for lensless imaging to achieve high image resolution in the imaging system [1], with a space–bandwidth product larger than that of lens-based setups [2]. Since no lens is required, this approach is cost effective and possible to be embedded in portable devices [3]. Lensless imaging has been applied to different disciplines, such as crystallography [4], material science [5], and biological imaging [6]. It mainly takes advantage of the diffraction process, which can encode the object information in captured data.

Among different configurations for lensless imaging, coherent diffractive imaging (CDI) is a powerful one with a simple imaging setup [7]. The object is illuminated with a coherent light source, and an imaging sensor is used to capture its far-field intensity image. Compared with conventional imaging setups, the imaging resolution of CDI is limited by the wavelength of the coherent light instead of the property of the lens. If coherent light with an ultrashort wavelength, such as X-rays, is used, the resolution can be greatly improved.

Although the optical setup for CDI is quite simple, the captured image is only the intensity pattern in the far field. Hence, an important step in the reconstruction algorithm, called phase retrieval, is required to retrieve the lost phase information from the interference fringes [8]. However, due to the non-uniqueness of the phase retrieval problem, some prior constraints in the object plane and imaging plane are required in most phase retrieval algorithms [9]. Some widely used constraints in the object plane are the size and location of the object [10].

Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you！Sign up now

When the structure of the object is complicated, these simple constraints are not sufficient to obtain satisfactorily reconstructed images. Conventional phase retrieval methods, such as the hybrid input–output (HIO) method [8], need many iterations and a good initial guess to solve this problem. There also exist some first-order algorithms for phase retrieval. Most are also iterative methods, such as the alternating direction method of multipliers (ADMM) [11 –14], shrinkage or thresholding algorithms [15,16], and proximal algorithms [17,18]. However, some of these methods consider only the case in which latent images are real-valued, while in real applications, they are often complex-valued, and the phase information is also important. Also, most of them adopt different kinds of prior knowledge for regularization, such as a deep denoiser [15], $ℓ_{1}$ or related regularization functions [16], but nearly all of them consider only natural images, which may not be efficient for the latent images in CDI. Deep learning methods can also be used for phase retrieval [19,20], but they need sufficient training images or accurate imaging models to generate synthetic training images.

The phase retrieval problem has also been investigated from the perspective of signal processing and optimization. The general problem they consider is the coded diffraction pattern (CDP) setup [21], which goes beyond the conventional CDI model with only the Fourier transform of the object. In this setup, different patterns are used as sensing matrices to spread the frequency information of a target, making it easier to reconstruct computationally with multiple measurements. A variety of phase retrieval algorithms are designed based on this, such as Wirtinger flow (WF) and its variants [22,23], Gauss–Newton method [24], spectral method [25], alternating minimization [26], and majorization–minimization [27]. These methods often have some restrictions on the sensing matrices or target objects. For example, sensing matrices are required to follow the Gaussian model [22,25,26], to be complete bases of the sensing space [24], or the target object is sparse [23]. Usually, more efforts are needed in designing optical systems to meet these requirements.

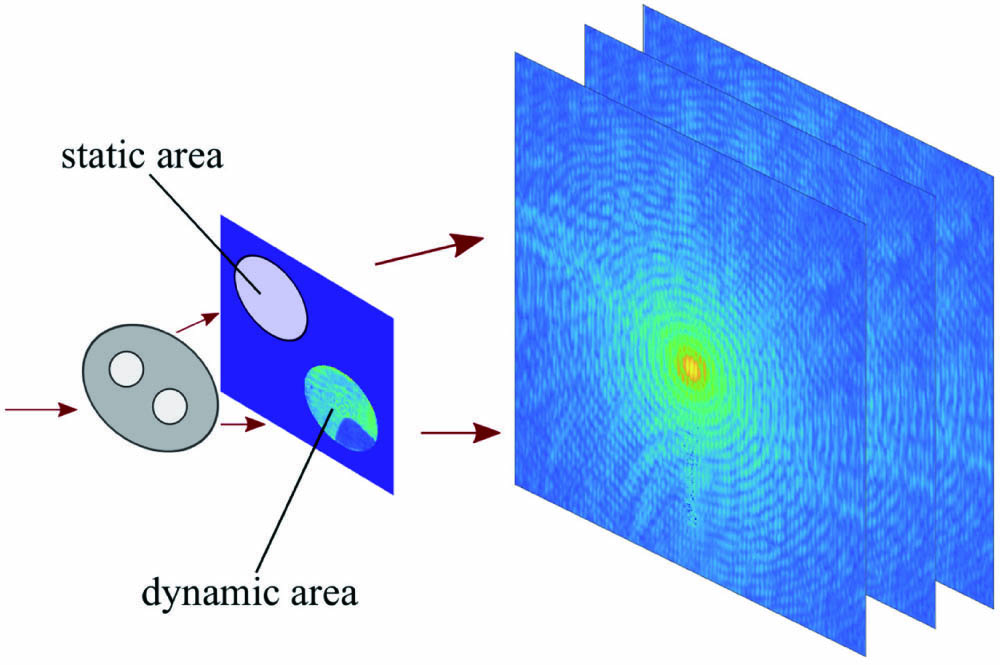
To take advantage of more accurate prior knowledge, it is possible to add some pre-designed strong constraints in the imaging systems directly. Some encoding masks, such as diffuser [28,29] and phase masks [30], can provide additional information to help with the reconstruction process. These coding elements are often hand-crafted with some prior knowledge, which shows the possibility of designing higher-resolution imaging systems for specific applications. For example, a simple masked CDI setup with an additional static area in the object plane, known as in situ CDI [31], is shown in Fig. 1. A dual pinhole is set in front of the object plane (middle plane in Fig. 1) to split the coherent light into two paths. One region on the object plane provides a static area in the imaging process, which can be regarded as efficient and solid prior knowledge in the object plane. The other part on the object plane is the sample area, which is dynamic. The imaging sensor is set in the far field to capture the oversampled Fourier intensity images. The image reconstruction problem for in situ CDI is to recover images of the dynamic area from the captured intensity images with the help of the static area. In these masked CDI setups, more prior knowledge can be used for algorithm design, which can improve the quality, robustness, and speed of reconstruction.

Typical masked CDI: in situ CDI setup [31].

Figure 1.Typical masked CDI: in situ CDI setup [31].

The main contributions of this paper are summarized as follows. •We propose a phase retrieval algorithm for masked CDI using ADMM. The proposed ADMM is in a plug-and-play (PnP) style, allowing for different hand-crafted or learning-based regularization functions with respect to complex-valued latent images.•Since the commonly used regularization functions in computational phase retrieval algorithms are designed or trained for real-valued natural images only, they are not suitable for complex-valued images in masked CDI experiments. We therefore design a regularization function based on the structure tensor and Harris corner detector in the complex domain.•We test our algorithm on real in situ CDI data, and the experimental results show that our method can achieve comparable results with the baseline method presented in Ref. [31], but the processing speed is $\sim 100 \times$ faster per frame. Our method is also more robust even for the single diffraction pattern phase retrieval problem.

2. PRINCIPLES AND METHODS

A. Foundation of the Inverse Problem

In a masked CDI setup, coherent light illuminates a coded aperture $p (x, y)$ and then transmits to the object plane. The incident light $l_{i} (x, y)$ can be calculated by the Fresnel diffraction integral [32] $l_{i} (x, y) = \frac{e^{j k z_{i}}}{j λ z_{i}} \iint_{- \infty}^{+ \infty} \exp {\frac{j k}{2 z_{i}} [{(x - ξ)}^{2} + {(y - η)}^{2}]} d ξ d η,$ (1)where $z_{i}$ is the distance between the mask and the object plane, $k$ is the wavenumber, and $λ$ is the wavelength. The transmissivity $\hat{u} (x, y)$ of the whole object plane can be represented as $\hat{u} (x, y) = a (x, y) e^{j θ (x, y)},$ (2)where $a (x, y)$ is the amplitude modulation, and $θ (x, y)$ is the phase shift. In this work, we consider a more general mathematical model with respect to the whole object plane. We assume that in a masked CDI setup, the object plane is partially known, which is called the static region, and it remains static during the whole imaging process. Also, the location of the unknown object is fixed in a known region of interest, which is called a dynamic region, i.e., image of the object we are concerned with, and its content changes in different experiments. These two regions do not overlap with each other.

The whole object plane is composed of these two parts. A background mask $m_{b} (x, y)$ and an object mask $m_{o} (x, y)$ indicate the locations of the static region and dynamic region on the object plane, respectively, such that $\hat{u} (x, y) = m_{b} (x, y) r (x, y) + m_{o} (x, y) u (x, y),$ (3)where $r (x, y)$ is the transmissivity of the pinhole or other known patterns, and $u (x, y)$ is the transmissivity of the object of interest. Note that if the background mask $m_{b}$ is a zero matrix, then this model will revert to the conventional CDI model, where only the location and shape of the target object are known. In this algorithm, we incorporate the prior knowledge related to the static area into the algorithm design as a strong constraint, which can help with the reconstruction process.

After the object is illuminated by the incident light, the emergent light $l_{e} (x, y)$ can be obtained as $l_{e} (x, y) = l_{i} (x, y) \hat{u} (x, y) .$ (4)Then, it propagates to the far-field detector plane such that $l_{o} (x, y) = F {l_{e} (x, y)},$ (5)where $F {\cdot}$ is the discrete Fourier transform. The captured image on the sensor is intensity only: $o (x, y) = | l_{o} (x, y) | .$ (6)The task is to reconstruct $u (x, y)$ from $o (x, y)$ with the known masks $m_{b}, m_{o}$ , static pattern $r$ , and the probe $l_{i}$ . This is the basic inverse imaging problem for the masked CDI setup, which is ill posed and non-convex.

B. ADMM with a Plug-and-Play Style for Masked CDI

For convenience, all the 2D matrices, such as $o (x, y)$ , are vectorized and represented by their bold variables, such as $o$ . The imaging model can be represented in a more compact form: $o = | F L (W_{b} r + W_{o} u) |,$ (7)where $L = diag (l_{i}), W_{b} = diag (m_{b})$ , $W_{o} = diag (m_{o})$ , and $F$ is the discrete Fourier transform matrix with a proper dimension. If the phase information $ϕ$ of the captured image $o$ is obtained, $u$ can easily be derived by the inverse step. We note that this model can also be regarded as a specific CDP setup, where the system matrix $A$ in the masked CDI setup is actually $A = F L W_{o}$ . However, as summarized in Section 1, the general methods designed for the CDP setup have some requirements on the property of the system matrix $A$ , such as the i.i.d. Gaussian assumption. In the masked CDI setup, the system matrix $A = F L W_{o}$ does not satisfy these requirements, making these methods less efficient for the masked CDI setup directly.

In real applications, the capturing process of many imaging devices, such as CCDs, is subject to various signal-dependent and signal-independent errors, which can be represented by a Poisson–Gaussian noise model [33]. This is typically handled by denoising [33] or introducing a strong regularization prior [34]. As the solution of a phase retrieval problem is not unique and the noise model should be taken into consideration, we introduce a regularization function $R (\cdot)$ to find a proper solution with respect to the prior knowledge [35]. Then, phase retrieval for masked CDI becomes an optimization problem: $minimize R (u) + C (ϕ) subject to F L \hat{u} = o \circ ϕ \hat{u} = W_{b} r + W_{o} u,$ (8)where $\circ$ is the Hadamard product, and $C (ϕ)$ is an indicator function to make the modulus of the elements in $ϕ$ equal to one, i.e., $C (ϕ) = {\begin{cases} 0, & | ϕ | = 1 \\ \infty, & otherwise \end{cases} .$ (9)Note that this function is a circle in the complex plane, which is non-convex. For simplicity, we consider the setup in which the two masks are binary masks, and then $u$ can be directly obtained from $\hat{u}$ as $u = W_{o} (\hat{u} - W_{b} r) .$ (10)Since $m_{o}$ and $m_{b}$ do not overlap, $W_{o} W_{b}$ is a zero matrix. This means that when calculating $u$ , we do not need the exact value of $r$ , but $\hat{u}$ is dependent on $r$ .

The whole optimization problem we are trying to solve can be written as $minimize R (u) + C (ϕ) subject to F L \hat{u} = o \circ ϕ, u = W_{o} (\hat{u} - W_{b} r) .$ (11)ADMM [36] can be used to solve this problem iteratively. First, using the Lagrange multiplier, the augmented Lagrangian is $L (\hat{u}, ϕ, u, λ, μ) = R (u) + C (ϕ) + \frac{ρ}{2} {‖ F L \hat{u} - o \circ ϕ + λ ‖}_{2}^{2} + \frac{τ}{2} {‖ u - W_{o} (\hat{u} - W_{b} r) + μ ‖}_{2}^{2},$ (12)where $λ$ and $μ$ are the Lagrange multipliers, and $ρ$ and $τ$ are the penalty parameters. ADMM can minimize $L$ by considering different variables separately. Only one variable is updated in each step. For example, in the $(k + 1)$ th iteration, when variable $\hat{u}$ is updated, other variables $ϕ, u, λ, μ$ are regarded as constants with their current values. The $\hat{u}$ -update step aims at solving a sub-problem: ${\hat{u}}^{(k + 1)} = \underset{\hat{u}}{argmin} L (\hat{u}, ϕ^{(k)}, u^{(k)}, λ^{(k)}, μ^{(k)}) .$ (13)Then a necessary condition for ${\hat{u}}^{(k + 1)}$ is ${\nabla_{\hat{u}} L (\hat{u}, ϕ^{(k)}, u^{(k)}, λ^{(k)}, μ^{(k)}) |}_{\hat{u} = {\hat{u}}^{(k + 1)}} = 0 .$ (14)In the complex domain, the required derivatives are regarded as Wirtinger derivatives [37]. The partial derivative of $L$ with respect to variable $\hat{u}$ is $\nabla_{\hat{u}} L = ρ {(F L)}^{H} (F L \hat{u} - o \circ ϕ + λ) + τ W_{o}^{H} (W_{o} \hat{u} - u - W_{o} W_{b} r - μ) .$ (15)After setting Eq. (15) to zero and substituting other variables with their current values, we can obtain the $\hat{u}$ -update step as ${\hat{u}}^{(k + 1)} = {(ρ L^{H} F^{H} F L + τ W_{o}^{H} W_{o})}^{- 1} [ρ {(F L)}^{H} (o \circ ϕ^{(k)} - λ^{(k)}) + τ W_{o}^{H} (u^{(k)} + W_{o} W_{b} r + μ^{(k)})] .$ (16)

Similarly, other update steps are $ϕ^{(k + 1)} = P_{o} (λ^{(k)} + F L {\hat{u}}^{(k + 1)}),$ (17) $u^{(k + 1)} = {prox}_{\frac{R}{τ}} [W_{o} ({\hat{u}}^{(k + 1)} - W_{b} r - μ^{(k)})],$ (18) $λ^{(k + 1)} = λ^{(k)} + F L {\hat{u}}^{(k + 1)} - o \circ ϕ^{(k + 1)},$ (19) $μ^{(k + 1)} = μ^{(k)} + u^{(k + 1)} - W_{o} ({\hat{u}}^{(k + 1)} - W_{b} r),$ (20)where $P_{o}$ is a projection operator defined as $P_{o} (s)_{(i)} = {\begin{matrix} \frac{s_{(i)} / o_{(i)}}{‖ s_{(i)} / o_{(i)}}, & o_{(i)} \neq 0, s_{(i)} \neq 0 \\ 1, & otherwise \end{matrix} .$ (21)Variable $i$ refers to the $i$ th element, and $prox (\cdot)$ is the proximal operator defined as [38] ${prox}_{\frac{R}{τ}} (v) = \underset{x}{argmin} (R (x) + \frac{τ}{2} ‖ x - v ‖) .$ (22)The proposed ADMM algorithm for masked CDI is summarized in Algorithm 1. Algorithm 1.

PnP-ADMM for Masked CDI

Input:

o

: captured diffraction pattern;

L

: probe;

W_{o}, W_{b}

: dynamic and static masks;

r

: known static pattern;

R

: regularization function;

{\hat{u}}^{(0)}, ϕ^{(0)}, u^{(0)}, λ^{(0)}, μ^{(0)}

: initial values;

ρ

τ

: penalty parameters;

ϵ_{tol}

: error tolerance.

Output: optimal reconstructed image

u^{*}

1: repeat

{\hat{u}}^{(k + 1)} = {(ρ L^{H} F^{H} F L + τ W_{o}^{H} W_{o})}^{- 1} [ρ {(F L)}^{H} (o \circ ϕ^{(k)} - λ^{(k)})

+ τ W_{o}^{H} (u^{(k)} + W_{o} W_{b} r + μ^{(k)})]

;

ϕ^{(k + 1)} = P_{o} (λ^{(k)} + F L {\hat{u}}^{(k + 1)})

;

u^{(k + 1)} = {prox}_{\frac{R}{τ}} [W_{o} ({\hat{u}}^{(k + 1)} - W_{b} r - μ^{(k)})]

;

λ^{(k + 1)} = λ^{(k)} + F L {\hat{u}}^{(k + 1)} - o \circ ϕ^{(k + 1)}

;

μ^{(k + 1)} = μ^{(k)} + u^{(k + 1)} - W_{o} ({\hat{u}}^{(k + 1)} - W_{b} r)

8: until

(\frac{‖ u^{(k + 1)} - u^{(k)} ‖_{2}}{‖ u^{(k + 1)} ‖_{2}} < ϵ_{tol})

C. Regularization Functions

We have developed the ADMM algorithm in a plug-and-play style, allowing for different kinds of regularization functions. Here, we investigate regularization functions that are efficient for denoising complex-valued images.

1. Regularization by Denoising

Regularization by denoising (RED) is a commonly used method of designing regularization functions according to the denoisers, instead of using denoisers directly to minimize some implicit functions [39]. In particular, the regularization function is designed as $R (x) = x^{H} [x - D (x)],$ (23)where $D (\cdot)$ is any proper denoiser. In the real domain, this function penalizes the residual $x - D (x)$ and the correlation with latent images at the same time, which is shown to be efficient [15,40].

Now, we consider the case $x = x_{r} + j x_{i}$ , where $x_{r}$ and $x_{i}$ are the real and imaginary parts, respectively. If $D (\cdot)$ is a learned denoiser, then for complex-valued images, the real and imaginary parts are regarded as two channels. The regularization function is $R (x) = (x_{r} + j x_{i})^{H} {[x_{r} - D (x_{r})] + j [x_{i} - D (x_{i})]} .$ (24)This regularization function is not real-valued. Hence, it is not suitable to be used directly for regularization.

Even using trained denoisers cannot help to solve this problem. If the useful information is related only to phase information $x_{p}$ instead of amplitude information $x_{a}$ , then the real and imaginary parts are $x_{a} \circ \sin x_{p}$ and $x_{a} \circ \cos x_{p}$ , respectively. After trigonometric transformations, the prior knowledge for natural images is not suitable for the real and imaginary parts anymore. Hence, we need to design new regularization functions for complex-valued images directly based on some statistical properties.

2. Quadratic Regularization Functions

In this work, we use the quadratic smoothing method [41], and the regularization function is designed as a quadratic penalty function: $R (x) = γ x^{H} Q x,$ (25)where $Q$ is a real-valued positive semi-definite matrix. For example, if $Q$ is selected as an identity matrix, then the regularization function is a simple $ℓ_{2}$ norm, which minimizes the transmitted energy.

The structure tensor, also known as the second-moment matrix, is useful for image filtering, holography, feature tracking, etc. [42 –44]. The original structure tensor is defined as $S = G * (\nabla u \nabla u^{H}),$ (26)where $\nabla$ is the $2 D$ differential operator, and $G$ is a Gaussian kernel for smoothing [45]. Generally, at each location $(x_{0}, y_{0})$ , this matrix has two eigenvalues $g_{1}$ and $g_{2}$ (assume $| g_{1} | \geq | g_{2} |$ ). When both $| g_{1} |$ and $| g_{2} |$ are small, there are only small variations in the neighborhood of this location, which means that this region is homogeneous. If $| g_{1} |$ is significantly larger than $| g_{2} |$ , then there is only large variation in a dominate direction, which is the edge region. If $| g_{1} |$ and $| g_{2} |$ are both large, then this location has high variations in all directions, which means it is close to an image corner. The complexity of the structure for an image is highly related to the number of edges and corners inside. To avoid the explicit eigenvalue decomposition of the structure tensor, the Harris corner detector [46] adopts the trace and determinant to design the edge and corner responses.

Following the idea of a structure tensor and Harris corner detector, since we want to find the solution with the simplest structure in the solution set, we need to care about only the trace of the structure tensor and make it as small as possible to construct more homogeneous areas. Hence, we select $Q$ as a 2D Laplacian operator matrix, and the quadratic structure is then suitable for smoothing. The regularization function is now the sum of the traces of all structure tensors in each location, which can help to find a proper solution with the simplest structure.

There are also some other regularization functions that can construct homogeneous areas, such as total variation (TV) and its variants [47], and wavelet transform [48]. Compared with the quadratic regularization functions, the proximal operators of these functions have more complicated expressions. Most of them are designed based on the $ℓ_{1}$ norm, whose proximal operator is a soft-thresholding function. We need to transfer these operators to the complex domain from the real domain, before embedding in the PnP-ADMM method.

3. EXPERIMENTS

A. Imaging Setup

To assess the efficiency of our method, we make use of the experimental in situ CDI data collected by Ref. [31]. The dataset consists of two optical experiments. The first experiment is an application in material science. In situ CDI is used to capture the growth of Pb dendrites on electrodes immersed in $Pb {({NO}_{3})}_{2}$ . A 543 nm He–Ne laser with a power of 5 mW is used to generate a collimated beam with a diameter of 800 μm. A dual pinhole aperture with two 100 μm circle holes spaced 100 μm apart is directly illuminated, and then the electro-chemical cell is 400 μm downstream of the aperture. A sealed fluid cell was assembled to observe the dynamics of Pb dendrites and separate it from the static area. An objective lens with 35 mm focal length is placed just downstream of the cell. One pinhole is placed in front of the cell, and another pinhole is focused on the region without any dendrite. A 12 V direct current source is applied to the cell. Finally, a CCD detector with $1340 \times 1300 pixels$ resolution and $20 \times 20 μm$ pixel size is used to capture images at the back focal plane of the lens. The location of the CCD detector is static, making the object-to-sensor distance the same for all diffraction patterns. A $5 \times 5$ ptychography is required for each image. Another experiment is related to biological imaging. In situ CDI is adopted to monitor the activation of glioblastoma cells. The same He–Ne laser is used to illuminate the live glioblastoma cells sealed between two cover slips. The same ptychography is also required.

B. Algorithm Setup

The parameters in ADMM are set as $ρ = τ = 1.0$ and $γ = 0.01$ , where the penalty parameters are set to be sufficiently large according to the convergence analysis in Ref. [49]. In the Pb growth experiment, the error tolerance is set as $ϵ_{tol} = 0.7$ . In the glioblastoma experiment, the error tolerance is set as $ϵ_{tol} = 0.25$ . The initial guess of the phase $ϕ^{(0)}$ is a vector with all elements equal to one, ${\hat{u}}^{(0)}$ is initialized as the union of the two masks multiplied by the probe, with reference to the spectral initialization commonly used for the CDP setup [25,50], and all the other vectors are initialized as zero.

According to the imaging setup of in situ CDI, some prior information is provided in the dataset. The two binary masks $m_{b}$ and $m_{o}$ are given with reference to the structure of the dual pinhole. The incident light on the object plane, called the probe, is also known. The task is to reconstruct the complex-valued image of the object using prior knowledge and the diffraction patterns. We compare our algorithm with a baseline algorithm that is also available online [31]. Both algorithms are implemented in MATLAB on a computer with Intel Core i5-8500 CPU at 3.00 GHz and 16 GB RAM.

C. Pb Growth Experiment

We first test our algorithm with the Pb growth experiment. In this case, the amplitude information shows the growth of Pb dendrites. The reconstruction results of ADMM and the baseline method are shown in Fig. 2. Different columns are imaging results with only intensity information at different times in the whole experiment. Imaging results of the Pb dendrites (blue part in the circle region) are almost identical using these two methods.

$Imaging results of the Pb growth experiment (amplitude reconstructions). (a)–(f), (m)–(r) ADMM phase retrieval results for No. 1–12 diffraction patterns; (g)–(l), (s)–(x) phase retrieval results for No. 1–12 diffraction patterns using the baseline method, respectively.$

Figure 2.Imaging results of the Pb growth experiment (amplitude reconstructions). (a)–(f), (m)–(r) ADMM phase retrieval results for No. 1–12 diffraction patterns; (g)–(l), (s)–(x) phase retrieval results for No. 1–12 diffraction patterns using the baseline method, respectively.

Then we introduce two metrics to evaluate the convergence property of ADMM. The R-factor evaluates the difference between reconstructed images and captured images in the measurement domain as $R (\hat{u}, o) = {‖ | F L \hat{u} | - o ‖}_{2} .$ (27)The relative error is defined as $ϵ_{rel}^{(k + 1)} = \frac{{‖ u^{(k + 1)} - u^{(k)} ‖}_{2}}{‖ u^{(k + 1)} ‖_{2}},$ (28)which shows the updates during the iterations. Note that for phase retrieval, we can recover the signal only up to a constant global phase shift $ϕ_{0}$ as $u^{*} e^{j ϕ_{0}}$ , compared with the true value $u^{*}$ . However, as we cannot obtain the value of $u^{*}$ or $u^{*} e^{j ϕ_{0}}$ in advance, we need to rely on the relative error $ϵ_{rel}^{(k + 1)}$ between two successive iterations to determine when to terminate the iteration process. We normally do so when it is smaller than a given tolerance, and the current solution is regarded as a stable solution. The R-factor and the relative error during ADMM iterations are shown in Fig. 3. We can see that both converge quickly. Since in real optical experiments, the optical conditions of the static area are not always the same as the known pattern (see Fig. 4), they do not converge to zero. Although these two planes are not the same, the main illumination patterns in the support area are similar.

$ADMM iterations for the Pb growth experiment (different colors for different diffraction patterns). Both converge quickly. (a) Error. (b) R-factor.$

Figure 3.ADMM iterations for the Pb growth experiment (different colors for different diffraction patterns). Both converge quickly. (a) Error. (b) R-factor.

$Reconstructed object planes for No. 1 diffraction pattern. The main difference is the area outside the support. (a) ADMM. (b) Baseline.$

Figure 4.Reconstructed object planes for No. 1 diffraction pattern. The main difference is the area outside the support. (a) ADMM. (b) Baseline.

To examine whether the proposed method can achieve comparable results with the baseline method, we calculate the relative peak signal-to-noise ratio (PSNR) and the structural similarity index (SSIM) [51] between the reconstruction results from ADMM and the baseline method, and the results are summarized in Table 1. All achieve $> 31 dB$ PSNR and $> 0.84$ SSIM. Visual results in Fig. 2 also show that the two methods can achieve comparable image quality in this experiment.Table 1.

Numerical Comparison between ADMM and Baseline Method for Pb Growth Experiment

No.	1	2	3	4	5	6
PSNR (dB)	31.0	32.5	33.5	34.7	34.7	34.1
SSIM	0.88	0.85	0.84	0.86	0.86	0.86
No.	7	8	9	10	11	12
PSNR (dB)	34.0	33.4	33.7	34.3	33.6	33.1
SSIM	0.85	0.84	0.86	0.86	0.86	0.86

We also compare our method with some other classical phase retrieval methods, mainly WF-based methods [22,52]. The phase retrieval results for the No. 1 image of the WF method and the truncated WF (TWF) method are shown in Fig. 5. We can find that even for the object with the simplest structure (No. 1 diffraction pattern) in this experiment, WF-based methods cannot provide valid information related to the Pb growth status. These results also show that the restrictions on the sensing matrices, such as the Gaussian model, are important to the phase retrieval qualities of these methods.

$Imaging results of No. 1 diffraction pattern in the Pb growth experiment (amplitude reconstructions) using different phase retrieval methods. (a) Baseline. (b) ADMM. (c) WF. (d) TWF.$

Figure 5.Imaging results of No. 1 diffraction pattern in the Pb growth experiment (amplitude reconstructions) using different phase retrieval methods. (a) Baseline. (b) ADMM. (c) WF. (d) TWF.

D. Glioblastoma Experiment

In the glioblastoma imaging experiment, the phase images show the status of glioblastoma cells. We first investigate the convergence of the ADMM with the relative error and R-factor in Fig. 6. As before, since we optimize only the dynamic region, the R-factor does not converge to zero, but a certain non-zero value after several iterations.

$ADMM iterations for the glioblastoma experiment (different colors for different diffraction patterns). (a) Error. (b) R-factor.$

Figure 6.ADMM iterations for the glioblastoma experiment (different colors for different diffraction patterns). (a) Error. (b) R-factor.

Imaging results with only phase information at different times are shown in Fig. 7. From Figs. 7(a) to 7(f) and Figs. 7(m) to 7(r), we can see that the smaller cell on the right moved to the bigger one, and then they merged together in these images. ADMM results show good agreement with the baseline in situ CDI results. However, there are more artifacts in the latter. As we can see in Figs. 7(k), 7(l), 7(s), 7(t), and 7(u), these artifacts may even change the shape of the merged cell, which can bring disturbances to the observation. With ADMM, the cell images are much clearer with less background noise and simpler image structures.

$Imaging results of the glioblastoma experiment (phase reconstructions). (a)–(f), (m)–(r) ADMM phase retrieval results for No. 1–12 diffraction patterns; (g)–(l), (s)–(x) phase retrieval results for No. 1–12 diffraction patterns using the baseline method, respectively.$

Figure 7.Imaging results of the glioblastoma experiment (phase reconstructions). (a)–(f), (m)–(r) ADMM phase retrieval results for No. 1–12 diffraction patterns; (g)–(l), (s)–(x) phase retrieval results for No. 1–12 diffraction patterns using the baseline method, respectively.

To give clearer evaluations of the reconstructed phase images of these two methods, we calculate the TV loss [53] of all the images, and the results are summarized in Table 2. We can see that for all diffraction patterns, ADMM has lower TV loss than the baseline method, which means that it can achieve phase retrieval results with simpler structures.Table 2.

Mean Total Variation Loss of Different Methods for Glioblastoma Experiment

No.	1	2	3	4	5	6
ADMM	0.599	0.601	0.595	0.642	0.816	0.820
Baseline	0.846	0.822	0.869	0.940	1.372	1.527
No.	7	8	9	10	11	12
ADMM	0.818	0.811	0.779	0.722	0.705	0.648
Baseline	1.485	1.445	1.397	1.316	1.365	1.378

E. Processing Time

The baseline method for in situ CDI is an updated version of the HIO method [8], and the update step is by gradient descent. Compared with this, a main advantage of our method is its high speed. The processing time of these two methods for different in situ CDI experiments is shown in Tables 3 and 4 and Fig. 8. ADMM needs only less than 0.5 s for a single diffraction pattern, while the baseline method needs more than 30 s for the same pattern. Specifically, the processing time of the baseline method is $39.29 / 0.37 = 106.19$ times longer than that of ADMM in the Pb growth experiment, and $40.38 / 0.34 = 118.76$ times longer in the glioblastoma experiment. Both the WF and TWF methods need more than 900 s for one diffraction pattern.Table 3.

Processing Time of Different Algorithms in Pb Growth Experiment (Unit: s)

No.	1	2	3	4	5	6	7
ADMM	0.39	0.38	0.37	0.37	0.38	0.37	0.37
Baseline	39.41	40.74	38.80	39.10	39.29	38.96	39.23
No.	8	9	10	11	12	Avg	Var
ADMM	0.37	0.36	0.37	0.36	0.37	0.37	$7 \times 10^{- 5}$
Baseline	39.24	39.12	39.24	38.88	39.45	39.29	0.25

Table 4.

Processing Time of Different Algorithms in Glioblastoma Experiment (Unit: s)

No.	1	2	3	4	5	6	7
ADMM	0.35	0.34	0.34	0.33	0.33	0.34	0.33
Baseline	40.25	39.97	39.93	40.64	40.56	40.14	40.15
No.	8	9	10	11	12	Avg	Var
ADMM	0.34	0.34	0.34	0.34	0.34	0.34	$2 \times 10^{- 5}$
Baseline	41.09	39.76	40.56	40.00	41.50	40.38	0.27

Figure 8.Processing time in different experiments (unit: s). (a) Pb growth experiment. (b) Glioblastoma experiment.

In our method, we separate the whole optimization problem into several sub-problems that are easier to solve, where closed-form solutions are obtained for these sub-problems. Compared with the alternating methods between the image space and Fourier space, directly solving the inverse problem is more efficient. Although in one iteration ADMM uses the proximal method and is slower than the simple gradient descent step, it can converge with modest accuracy within a few iterations [36], while the baseline method needs many more iterations. Hence, our method is faster overall to give reconstructed images.

F. Phase Retrieval with Single Diffraction Pattern

In the two experiments above, ADMM does not take advantage of the relationship among different diffraction patterns, but the baseline method combines these patterns to update the static area in the object plane, based on the fact that this area is the same among different patterns during the experiment. In this section, we compare our ADMM method with the baseline method for phase retrieval with only one diffraction pattern available to the algorithms.

We randomly choose one diffraction pattern from the Pb growth experiment and glioblastoma experiment. The phase retrieval results for different algorithms with different kinds of objects are shown in Fig. 9. We can easily find that the performance of the baseline method drops significantly for both experiments. The reconstructed image in Fig. 9(a) is less clear than in Fig. 9(b), the ADMM result. For a phase-only object, the baseline method even diverges and cannot give any meaningful information in Fig. 9(c), while ADMM in Fig. 9(d) is not influenced by the reduction of diffraction patterns. An explanation for this is that ADMM does not care about the region outside the dynamic area or the static area in the object plane, since they are mainly caused by noise, pinhole diffraction, etc. [see Fig. 4(b)]. Hence, although the imaging model is actually $F L [W_{o} u + W_{b} r + (1 - W_{o} - W_{b}) n] = y \circ ϕ,$ (29)object $u$ is not related to disturbance $n$ , and we can solve the phase retrieval problem directly with existence of these disturbances as noise. However, the baseline method tries to find the exact value of $n$ and then $u$ , making the problem more complicated; hence, more diffraction patterns are required, and it does not perform well for the single diffraction pattern phase retrieval problem.

$Phase retrieval results with single diffraction pattern. (a), (b) Baseline method and ADMM method for No. 10 diffraction pattern in the Pb growth experiment; (c), (d) baseline method and ADMM method for No. 7 diffraction pattern in the glioblastoma experiment, respectively.$

Figure 9.Phase retrieval results with single diffraction pattern. (a), (b) Baseline method and ADMM method for No. 10 diffraction pattern in the Pb growth experiment; (c), (d) baseline method and ADMM method for No. 7 diffraction pattern in the glioblastoma experiment, respectively.

4. CONCLUSION

In summary, we present a fast and robust ADMM that can retrieve proper phase maps according to the diffraction patterns in masked CDI. Our method is plug-and-play, allowing for different kinds of regularization functions as prior knowledge. We also design quadratic regularization functions according to the structure tensor and Harris corner detector, which can denoise and find the simplest structure in the complex domain directly, instead of separating complex-valued images into real and imaginary parts, simplifying the algorithm design.

In optical experiments, we can see that compared with the conventional phase retrieval methods for masked CDI, our ADMM approach is much faster. Less background noise and clearer phase images further indicate the power of the designed regularization functions. Although the imaging results of Pb dendrites using the baseline method seem to have sharper edges with the help of the background patterns, in some more complicated cases, such as retrieving the phase of the phase-only objects in the glioblastoma experiment, the background patterns bring strong disturbances to the observation of the cells, making it less robust than ADMM. Our method also performs well even with a single diffraction pattern, showing the robustness of our method.

References

[1] S. Eisebitt, J. Lüning, W. F. Schlotter, M. Lörgen, O. Hellwig, W. Eberhardt, J. Stöhr. Lensless imaging of magnetic nanostructures by x-ray spectro-holography. Nature, 432, 885-888(2004).

[2] A. Ozcan, E. McLeod. Lensless imaging and sensing. Annu. Rev. Biomed. Eng., 18, 77-102(2016).

[3] T. Zeng, E. Y. Lam. Robust reconstruction with deep learning to handle model mismatch in lensless imaging. IEEE Trans. Comput. Imaging, 7, 1080-1092(2021).

[4] D. Sayre. Some implications of a theorem due to Shannon. Acta Crystallogr., 5, 843(1952).

[5] R. L. Sandberg, A. Paul, D. A. Raymondson, S. Hädrich, D. M. Gaudiosi, J. Holtsnider, R. I. Tobey, O. Cohen, M. M. Murnane, H. C. Kapteyn, C. Song, J. Miao, Y. Liu, F. Salmassi. Lensless diffractive imaging using tabletop coherent high-harmonic soft-X-ray beams. Phys. Rev. Lett., 99, 098103(2007).

[6] W. Harm, C. Roider, A. Jesacher, S. Bernet, M. Ritsch-Marte. Lensless imaging through thin diffusive media. Opt. Express, 22, 22146-22156(2014).

[7] J. Miao, P. Charalambous, J. Kirz, D. Sayre. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature, 400, 342-344(1999).

[8] J. R. Fienup. Phase retrieval algorithms: a comparison. Appl. Opt., 21, 2758-2769(1982).

[9] Y. Shechtman, Y. C. Eldar, O. Cohen, H. N. Chapman, J. Miao, M. Segev. Phase retrieval with application to optical imaging: a contemporary overview. IEEE Signal Process. Mag., 32, 87-109(2015).

[10] J. A. Rodriguez, R. Xu, C.-C. Chen, Y. Zou, J. Miao. Oversampling smoothness: an effective algorithm for phase retrieval of noisy diffraction intensities. J. Appl. Crystallogr., 46, 312-318(2013).

[11] D. S. Weller, A. Pnueli, G. Divon, O. Radzyner, Y. C. Eldar, J. A. Fessler. Undersampled phase retrieval with outliers. IEEE Trans. Comput. Imaging, 1, 247-258(2015).

[12] K. Huang, N. D. Sidiropoulos. Consensus-ADMM for general quadratically constrained quadratic programming. IEEE Trans. Signal Process., 64, 5297-5310(2016).

[13] P. Villanueva-Perez, F. Arcadu, P. Cloetens, M. Stampanoni. Contrast-transfer-function phase retrieval based on compressed sensing. Opt. Lett., 42, 1133-1136(2017).

[14] B. Shi, Q. Lian, X. Huang, N. An. Constrained phase retrieval: when alternating projection meets regularization. J. Opt. Soc. Am. B, 35, 1271-1281(2018).

[15] C. A. Metzler, P. Schniter, A. Veeraraghavan, R. G. Baraniuk. prDeep: robust phase retrieval with a flexible deep network. International Conference on Machine Learning, 3501-3510(2018).

[16] F. Momey, L. Denis, T. Olivier, C. Fournier. From Fienup’s phase retrieval techniques to regularized inversion for in-line holography: tutorial. J. Opt. Soc. Am. A, 36, D62-D80(2019).

[17] H. Yan. Ptychographic phase retrieval by proximal algorithms. New J. Phys., 22, 023035(2020).

[18] H. Chang, S. Marchesini, Y. Lou, T. Zeng. Variational phase retrieval with globally convergent preconditioned proximal algorithm. SIAM J. Imag. Sci., 11, 56-93(2018).

[19] A. Goy, K. Arthur, S. Li, G. Barbastathis. Low photon count phase retrieval using deep learning. Phys. Rev. Lett., 121, 243902(2018).

[20] G. Zhang, T. Guan, Z. Shen, X. Wang, T. Hu, D. Wang, Y. He, N. Xie. Fast phase retrieval in off-axis digital holographic microscopy through deep learning. Opt. Express, 26, 19388-19405(2018).

[21] E. J. Candes, X. Li, M. Soltanolkotabi. Phase retrieval from coded diffraction patterns. Appl. Comput. Harmon. Anal., 39, 277-299(2015).

[22] E. J. Candes, X. Li, M. Soltanolkotabi. Phase retrieval via Wirtinger flow: theory and algorithms. IEEE Trans. Inf. Theory, 61, 1985-2007(2015).

[23] T. T. Cai, X. Li, Z. Ma. Optimal rates of convergence for noisy sparse phase retrieval via thresholded Wirtinger flow. Ann. Stat., 44, 2221-2251(2016).

[24] B. Gao, Z. Xu. Phaseless recovery using the Gauss–Newton method. IEEE Trans. Signal Process., 65, 5885-5896(2017).

[25] W. Luo, W. Alghamdi, Y. M. Lu. Optimal spectral initialization for signal recovery with applications to phase retrieval. IEEE Trans. Signal Process., 67, 2347-2356(2019).

[26] P. Netrapalli, P. Jain, S. Sanghavi. Phase retrieval using alternating minimization. IEEE Trans. Signal Process., 63, 4814-4826(2015).

[27] T. Qiu, P. Babu, D. P. Palomar. PRIME: phase retrieval via majorization-minimization. IEEE Trans. Signal Process., 64, 5174-5186(2016).

[28] N. Antipa, G. Kuo, R. Heckel, B. Mildenhall, E. Bostan, R. Ng, L. Waller. DiffuserCam: lensless single-exposure 3D imaging. Optica, 5, 1-9(2018).

[29] T. Zeng, E. Y. Lam. Model-based network architecture for image reconstruction in lensless imaging. Proc. SPIE, 11551, 115510B(2020).

[30] I. Johnson, K. Jefimovs, O. Bunk, C. David, M. Dierolf, J. Gray, D. Renker, F. Pfeiffer. Coherent diffractive imaging using phase front modifications. Phys. Rev. Lett., 100, 155503(2008).

[31] Y. H. Lo, L. Zhao, M. Gallagher-Jones, A. Rana, J. J. Lodico, W. Xiao, B. Regan, J. Miao. In situ coherent diffractive imaging. Nat. Commun., 9, 1826(2018).

[32] J. W. Goodman. Introduction to Fourier Optics(2017).

[33] Y. Zhang, P. Song, Q. Dai. Fourier ptychographic microscopy using a generalized anscombe transform approximation of the mixed Poisson-Gaussian likelihood. Opt. Express, 25, 168-179(2017).

[34] I. Kang, F. Zhang, G. Barbastathis. Phase extraction neural network (PhENN) with coherent modulation imaging (CMI) for phase retrieval at low photon counts. Opt. Express, 28, 21578-21600(2020).

[35] Z. Xu, E. Y. Lam. Maximum a posteriori blind image deconvolution with Huber-Markov random-field regularization. Opt. Lett., 34, 1453-1455(2009).

[36] S. Boyd, N. Parikh, E. Chu. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers(2011).

[37] R. Remmert. Theory of Complex Functions(1991).

[38] N. Parikh, S. Boyd. Proximal algorithms. Found. Trends Optim., 1, 127-239(2014).

[39] Y. Romano, M. Elad, P. Milanfar. The little engine that could: regularization by denoising (RED). SIAM J. Imag. Sci., 10, 1804-1844(2017).

[40] Z. Wu, Y. Sun, J. Liu, U. Kamilov. Online regularization by denoising with applications to phase retrieval. Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, 1-9(2019).

[41] M. Pham, P. Yin, A. Rana, S. Osher, J. Miao. Generalized proximal smoothing (GPS) for phase retrieval. Opt. Express, 27, 2792-2808(2019).

[42] J. Weickert. Coherence-enhancing diffusion filtering. Int. J. Comput. Vis., 31, 111-127(1999).

[43] S. Lefkimmiatis, A. Roussos, P. Maragos, M. Unser. Structure tensor total variation. SIAM J. Imag. Sci., 8, 1090-1122(2015).

[44] Z. Ren, E. Y. Lam, J. Zhao. Acceleration of autofocusing with improved edge extraction using structure tensor and Schatten norm. Opt. Express, 28, 14712-14728(2020).

[45] J. Angulo. Structure tensor image filtering using Riemannian ℓ₁ and ℓ_∞ center-of-mass. Image Anal. Stereol., 33, 95-105(2014).

[46] C. Harris, M. Stephens. A combined corner and edge detector. Alvey Vision Conference, 147-151(1988).

[47] V. Caselles, A. Chambolle, M. Novaga. Total variation in imaging. Handbook of Mathematical Methods in Imaging, 1, 1455-1499(2015).

[48] M. J. Shensa. The discrete wavelet transform: wedding the a trous and Mallat algorithms. IEEE Trans. Signal Process., 40, 2464-2482(1992).

[49] Y. Wang, W. Yin, J. Zeng. Global convergence of ADMM in nonconvex nonsmooth optimization. J. Sci. Comput., 78, 29-63(2019).

[50] Y. M. Lu, G. Li. Spectral initialization for nonconvex estimation: high-dimensional limit and phase transitions. IEEE International Symposium on Information Theory (ISIT), 3015-3019(2017).

[51] Z. Wang, A. C. Bovik, H. R. Sheikh, E. P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process., 13, 600-612(2004).

[52] Y. Chen, E. J. Candès. Solving random quadratic systems of equations is nearly as easy as solving linear systems. Commun. Pure Appl. Math., 70, 822-883(2017).

[53] Y. Li, F. Santosa. A computational algorithm for minimizing total variation in image restoration. IEEE Trans. Image Process., 5, 987-995(1996).

[54] https://www.physics.ucla.edu/research/imaging/ISCDI/. https://www.physics.ucla.edu/research/imaging/ISCDI/