While deep learning has demonstrated tremendous potential for photonic device design, it often demands a large amount of labeled data to train these deep neural network models. Preparing these data requires high-resolution numerical simulations or experimental measurements and cost significant, if not prohibitive, time and resources. In this work, we present a highly efficient inverse design method that combines deep neural networks with a genetic algorithm to optimize the geometry of photonic devices in the polar coordinate system. The method requires significantly less training data compared with previous inverse design methods. We implement this method to design several ultra-compact silicon photonics devices with challenging properties including power splitters with uncommon splitting ratios, a TE mode converter, and a broadband power splitter. These devices are free of the features beyond the capability of photolithography and generally in compliance with silicon photonics fabrication design rules.
- Photonics Research
- Vol. 9, Issue 6, B247 (2021)
Abstract
1. INTRODUCTION
The advent of photonic integrated circuits (PICs) is expected to revolutionize many industries such as optical interconnects [1–3], optical sensing [3–6], and optical computing [7,8]. The progress of PICs demands compact photonic devices with a variety of properties to increasingly integrate more functionality on a chip. The property of a photonic device is highly determined by its geometry, which is usually designed and optimized by an experienced photonic designer based on intuition and numerical simulations. This traditional method is limited by designers’ experience and usually only applies to the designs with simple geometric structures. However, complex geometries are often required for realizing ultra-compact photonic devices with challenging properties. The design of these complex structures with a large number of parameters is beyond the capability of human intuition and demands more efficient methods. The brute force optimization method is impractical, as the numerical simulation algorithms, such as the finite-difference time-domain (FDTD) method, are very computation intensive and time consuming. Traditional regression-based optimization methods face difficulties in convergence due to the high-dimensional parameter space. A variety of inverse design methods such as level set methods, adjoint method, local-optimization techniques, and direct-binary search [9–19] have been developed to tackle this issue. These methods expand the design space and realize many photonic devices with complex and nonintuitive structures that present extraordinary properties. Fundamentally, these algorithms are rule-based approaches containing iterative searching steps in a case-by-case manner, often relying on numerical simulations in each step to produce intermediate results that help to modify the searching strategy. Such stochastic algorithms are limited by their random-search nature and are insufficient for complex designs in a multi-constrained problem [20–22].
This challenge may be addressed by deep learning (DL) and more specifically deep neutral networks (DNNs), which use many processing layers to learn the representations of data with multiple levels of abstraction [23]. DNN has been revolutionizing many fields, including image analysis [24], natural language processing [25], materials science [26], quantum physics [27], and so on. Neural network (NN)-based methods have previously been adopted in studying photonic devices such as phase delay structures [28], photonic crystal nanocavities [29], and nanophotonic particles [30]. However, applying a DNN to photonic device design faces a practical challenge of preparing a large training dataset [20]. For example, Ma et al. used an NN model trained on 30,000 device designs for a chiral metamaterial inverse design [31]; Tahersima
In this paper, we present a genetic-algorithm-based deep neural network (GDNN) method that requires an order of magnitude less simulation data (less than 3000 in the presented cases) for training. By using this approach, we have designed several silicon photonics devices including power splitters with uncommon splitting ratios, a TE mode converter, and a broadband power splitter. Besides high efficiency, the algorithm exhibits great flexibility and ability in dealing with multiple design constrains. For example, the broadband power splitter is designed for as many as 11 optimization targets, and the optimal design exhibits a maximum insertion loss of 0.47 dB and good flatness over 400 nm wavelength range with a
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
2. ALGORITHM
The GDNN-based inverse design algorithm developed in this work includes encoding, selection, and DNN-based forward and inverse design processes. The workflow of the algorithm is exhibited in Fig. 1. First, the device models and numerical simulation results of the initial device designs are encoded into a dataset called population (step A of Fig. 1). In mimicking the natural selection process, the population is selected with respect to an objective function (step B of Fig. 1). The whole population is also used to generate the weight parameters in the DNN models of both the forward design and the inverse design [step C (1) of Fig. 1]. The selection process produces an adaptive (good performance) generation as the parents to reproduce their offspring through the inverse design process [step C (2) of Fig. 1]. These offspring are then added to the initial population (step D of Fig. 1) and update the weights in the DNN models to start the next iteration. This process is repeated until the DNN model meets the required optimization target to the investigated design problem.
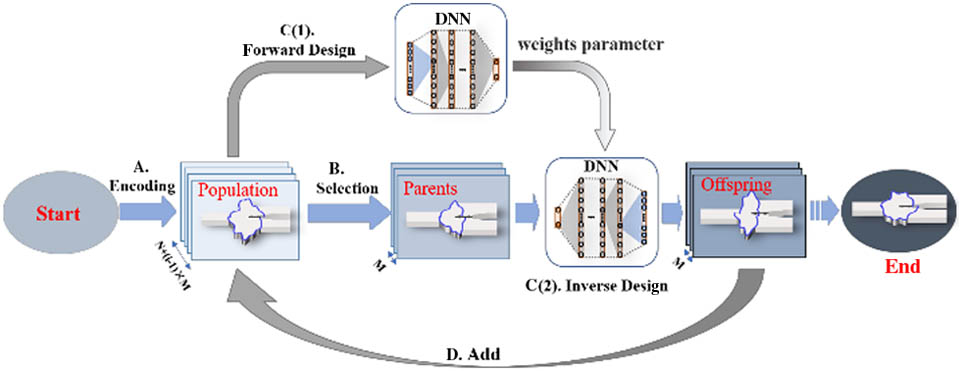
Figure 1.Workflow of the GDNN algorithm developed in this paper.
A. Encoding
The encoding process aims to map a physical problem, e.g., the output optical power of an optical device with multiple degrees of freedom in its physical structures, to a mathematical data structure. An encoded data structure represents a solution to the problem and affects the optimization process. In this work, each individual of the initial population is described with two sets of parameters. One set represents the encoded device physical structure that will be genetically optimized, and the other represents the investigated optical performance. The encoding process of a power splitter device is schematically shown in Fig. 2. An arbitrarily shaped one-by-two power splitter includes one input waveguide, two output waveguides, and a core that is described by its border line. By considering the device design rules and its symmetry, we adopt the polar coordinate system with its origin located on the center line and use two sets of polar vectors (
![]()
Figure 2.Encoding process that uses polar vectors and design rule constrains as a parameter vector to describe the design of a given photonic device.
B. Selection and DNN-Based Evolution
The population selection process is a prerequisite for DNN-based inversed design. It evaluates the FOM of each individual in the current population and selects a subset of the population with good values to be the parents that “reproduce” the next generation of device designs. Due to the “genetic” correlation between the parents and the offspring connected by the neural networks, additional factors can be added to the selection process to intentionally guide the direction of certain features in the evolution. For example, a punishment factor on the device area can be added to guide the algorithm to favor more compact designs.
A genetic algorithm mainly includes three operations: selection, crossover, and mutation. Crossover and mutation are the key steps to produce excellent offspring. In the GDNN algorithm, we use the DNN model to replace the crossover and mutation operations of the genetic algorithm. The DNN model can be inferred in both forward and inverse ways. The forward design process can obtain the device FOM and network weight parameters in the form of a given encoded design parameter vector. The network weight parameters are the key settings for enabling the reverse design process. The inverse design process after obtaining the network weight parameters utilizes the FOM data associated with wavelength as the input to produce offspring device designs that are correlated but different than the parent. The forward and the inverse design processes are schematically shown in Fig. 3. A fully connected multilayer DNN is used with the sigmoid activation function and back-propagation method for weight updates.
![]()
Figure 3.Schematic drawing of the DNN models of the forward and inverse design processes.
In the inverse design process, the cost function is represented by the error E of the FOM of a specific design (
3. SIMULATION RESULTS
In order to study its capability and performance, we applied the GDNN algorithm to design several very compact Si photonics devices as examples, including low-loss power splitters with specific unequal output powers, a TE mode converter, and a broadband power splitter. All of these devices are designed based on common Si photonics platforms with silicon-on-insulator (SOI) substrates with 220 nm device silicon and a 2–3 μm buried oxide (BOX) layer. The waveguide is 500 nm in width and operated at (or around) 1550 nm wavelength. All the devices are designed according to the process design rule that no line or space feature size is smaller than 0.2 μm.
We take a power splitter with splitting ratio of 2:3 as an example to quantitatively analyze the design process. The initial population is composed of 1000 device structures randomly generated according to the encoding process stated earlier. The distribution of total optical transmission of a typical random population is shown in Fig. 4(d). In this case, the majority of the population show very poor transmission, and only 1.5% transmit
![]()
Figure 4.Design analyses of a power splitter with splitting ratio of 2:3: (a) the evolution of the qualified population proportion; (b) and (c) the FDTD simulation result of the best devices in the initial population and the final population; (d) the distribution of optical transmission of the initial population.
Similar design processes are adopted to optimize the other optical devices including a 1:2 power splitter with 0.36 dB insertion loss and
![]()
Figure 5.GDNN design examples with transmission spectrum and FDTD simulation results: (a) a 1:2 power splitter, (b) a 1:1 power splitter, (c) a TE mode converter, and (d) a broadband power splitter.
4. DISCUSSIONS AND CONCLUSION
In this work, the DNN was implemented by using PyTorch, an open source machine learning framework. The same GDNN architecture is used for all the designs. The architecture includes 10 hidden layers with the dimension of 100. There are 1000 trained data for the initial population and 50 reproduced offspring for each iteration. The algorithm is implemented on a workstation with an AMD Ryzen 3700X CPU and a Nvidia GeForce RTX 2070 GPU. It takes about 6–10 h to complete the whole design including the FDTD simulation of the 1000 initial population data and the whole genetic optimization process.
DNN has been proved to be a powerful tool for designing optical devices using an inverse design process. Previous DNN-based inverse design algorithms usually require 20,000 to 40,000 training data [31,32], which take the majority of the design time due to the computation intensive high-resolution FDTD simulations. The use of genetic optimization reduces the number of the training data by an order of magnitude. In addition, unlike many inverse design algorithms, our GDNN algorithm does not require the initial data set to include a large amount of good performance designs because the quality of the population is iteratively improved during the evolution. In fact, we intentionally include some device designs, violating design rules that serve for regulating the constraints of the inverse design. As shown in Table 1, the GDNN uses 1000 sets of data for the initial training of the model. After that, 50 sets of offspring will be added to participate in the training of the model. It is worth mentioning that the model design with similar structural design uses the same set of initial datasets (1000 sets of data), for instance, power splitter (1:1) and broadband splitter, power splitter (1:2) and power splitter (2:3). Our GDNN algorithm completes a design task with less than 3000 design data including the 1000 initial population and the offspring of all iterations. This is an order of magnitude less than the training data for a typical previous inverse design algorithm.
Training Data Summary of the Designs in This Work
| Device Designs | Initial Data | Number of Iterations | Number of Offspring | Total Data |
|---|---|---|---|---|
| Power splitter (1:1) | 1000 | 35 | 50 | 2750 |
| Power splitter (1:2) | 1000 | 28 | 50 | 2400 |
| Power splitter (2:3) | 1000 | 32 | 50 | 2600 |
| TE mode converter | 1000 | 30 | 50 | 2500 |
| Broadband splitter | 1000 | 23 | 50 | 2150 |
In comparison, we have investigated using an efficiency-focused generative adversarial network (GAN) model to design the same photonic devices (2:3 power splitter). The results (Fig. 6) show that greater than 10,000 device design training data are required to achieve designs with comparable performance.
![]()
Figure 6.Comparison of GAN and GDNN design results.
In conclusion, by combining DNN with genetic evolution, our GDNN method exhibits great flexibility and efficiency in designing ultra-compact photonic devices with challenging properties. Compared with previous optimization algorithms, the GDNN algorithm is more capable of complex multi-constraint and multi-objective optimization. Without relying on pixelized features in a predefined geometry and grid, our method allows design of more flexible device structures while obeying fabrication design rules. The genetic evolution nature of the algorithm greatly increases computation efficiency and reduces FDTD training data by an order of magnitude compared with previous DNN-based inverse design methods. In addition, the genetic selection process allows introduction of biases to guide certain design directions such as a small footprint. To exhibit the capability of the method, we design several Si photonics devices including power splitters with uncommon splitting ratios, a TE mode converter, and a broadband power splitter. These devices are free of the features beyond the capability of photolithography and generally in compliance with silicon photonics fabrication design rules. We believe the presented GDNN algorithm can be widely implemented in designing many complex micro- and nanophotonic structures that could not be easily realized before.
Acknowledgment
Acknowledgment. The authors thank Dr. Shiyue Hua for helpful discussion.
References
[1] M. J. R. Heck, H. W. Chen, A. W. Fang, B. R. Koch, D. Liang, H. Park, M. N. Sysak, J. E. Bowers. Hybrid silicon photonics for optical interconnects. IEEE J. Sel. Top. Quantum Electron., 17, 333-346(2011).
[2] Y. Urino, T. Usuki, J. Fujikata, M. Ishizaka, K. Yamada, T. Horikawa, T. Nakamura, Y. Arakawa. High-density and wide-bandwidth optical interconnects with silicon optical interposers [Invited]. Photon. Res., 2, A1-A7(2014).
[3] Y. Li, Y. Zhang, L. Zhang, A. W. Poon. Silicon and hybrid silicon photonic devices for intra-datacenter applications: state of the art and perspectives. Photon. Res., 3, B10-B27(2015).
[4] J. Sun, E. Timurdogan, A. Yaacobi, E. S. Hosseini, M. R. Watts. Large-scale nanophotonic phased array. Nature, 493, 195-199(2013).
[5] X. Sun, L. Zhang, Q. Zhang, W. Zhang. Si photonics for practical LiDAR solutions. Appl. Sci., 9, 4225(2019).
[6] C. V. Poulton, M. J. Byrd, M. Raval, Z. Su, N. Li, E. Timurdogan, D. Coolbaugh, D. Vermeulen, M. R. Watts. Large-scale silicon nitride nanophotonic phased arrays at infrared and visible wavelengths. Opt. Lett., 42, 21-24(2017).
[7] J. Feldmann, N. Youngblood, C. D. Wright, H. Bhaskaran, W. H. P. Pernice. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature, 569, 208-214(2019).
[8] K. Vandoorne, P. Mechet, T. Van Vaerenbergh, M. Fiers, G. Morthier, D. Verstraeten, B. Schrauwen, J. Dambre, P. Bienstman. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun., 5, 3541(2014).
[9] K. Xu, L. Liu, X. Wen, W. Sun, N. Zhang, N. Yi, S. Sun, S. Xiao, Q. Song. Integrated photonic power divider with arbitrary power ratios. Opt. Lett., 42, 855-858(2017).
[10] E. Khoram, X. Qian, M. Yuan, Z. Yu. Controlling the minimal feature sizes in adjoint optimization of nanophotonic devices using b-spline surfaces. Opt. Express, 28, 7060-7069(2020).
[11] J. Lu, J. Vučković. Nanophotonic computational design. Opt. Express, 21, 13351-13367(2013).
[12] C. M. Lalau-Keraly, S. Bhargava, O. D. Miller, E. Yablonovitch. Adjoint shape optimization applied to electromagnetic design. Opt. Express, 21, 21693-21701(2013).
[13] B. Shen, P. Wang, R. Polson, R. Menon. An integrated-nanophotonics polarization beamsplitter with 2.4 × 2.4 μm2 footprint. Nat. Photonics, 9, 378-382(2015).
[14] D. Vercruysse, N. V. Sapra, L. Su, R. Trivedi, J. Vučković. Analytical level set fabrication constraints for inverse design. Sci. Rep., 9, 8999(2019).
[15] A. Y. Piggott, E. Y. Ma, L. Su, G. H. Ahn, N. V. Sapra, D. Vercruysse, A. M. Netherton, A. S. P. Khope, J. E. Bowers, J. Vučković. Inverse-designed photonics for semiconductor foundries. ACS Photon., 7, 569-575(2020).
[16] A. Y. Piggott, J. Lu, K. G. Lagoudakis, J. Petykiewicz, T. M. Babinec, J. Vucković. Inverse design and demonstration of a compact and broadband on-chip wavelength demultiplexer. Nat. Photonics, 9, 374-377(2015).
[17] C. Y. Kao, S. Osher, E. Yablonovitch. Maximizing band gaps in two-dimensional photonic crystals by using level set methods. Appl. Phys. B, 81, 235-244(2005).
[18] K. Wang, X. Ren, W. Chang, L. Lu, D. Liu, M. Zhang. Inverse design of digital nanophotonic devices using the adjoint method. Photon. Res., 8, 528-533(2020).
[19] J. C. C. Mak, C. Sideris, J. Jeong, A. Hajimiri, J. K. S. Poon. Binary particle swarm optimized 2 × 2 power splitters in a standard foundry silicon photonic platform. Opt. Lett., 41, 3868-3871(2016).
[20] W. Ma, Z. Liu, Z. A. Kudyshev, A. Boltasseva, W. Cai, Y. Liu. Deep learning for the design of photonic structures. Nat. Photonics, 15, 77-90(2020).
[21] W. Li, F. Meng, Y. Chen, Y. Fan Li, X. Huang. Topology optimization of photonic and photonic crystals and metamaterials: a review. Adv. Theor. Simul., 2, 1900017(2019).
[22] S. Molesky, Z. Lin, A. Y. Piggott, W. Jin, J. Vucković, A. W. Rodriguez. Inverse design in nanophotonics. Nat. Photonics, 12, 659-670(2018).
[23] Y. Lecun, Y. Bengio, G. Hinton. Deep learning. Nature, 521, 436-444(2015).
[24] B. A. Krizhevsky, I. Sutskever, G. E. Hinton. Image net classification with deep convolutional neural networks. Commun. ACM, 60, 84-90(2012).
[25] T. Young, D. Hazarika, S. Poria, E. Cambria. Recent trends in deep learning based natural language processing. IEEE Comput. Intell. Mag., 13, 55-75(2018).
[26] Y. Mao, Q. He, X. Zhao. Designing complex architectured materials with generative adversarial networks. Sci. Adv., 6, eaaz4169(2020).
[27] G. Carleo, M. Troyer. Solving the quantum many-body problem with artificial Neural networks. Science, 355, 602-606(2007).
[28] D. Liu, Y. Tan, E. Khoram, Z. Yu. Training deep neural networks for the inverse design of nanophotonic structures. ACS Photon., 5, 1365-1369(2018).
[29] T. Asano, S. Noda. Optimization of photonic crystal nanocavities based on deep learning. Opt. Express, 26, 32704-32717(2018).
[30] J. Peurifoy, Y. Shen, L. Jing, Y. Yang, F. Cano-Renteria, B. Delacy, M. Tegmark, J. D. Joannopoulos, M. Soljacić. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci. Adv., 4, eaar4206(2018).
[31] W. Ma, F. Cheng, Y. Liu. Deep-learning-enabled on-demand design of chiral metamaterials. ACS Nano, 12, 6326-6334(2018).
[32] M. H. Tahersima, K. Kojima, T. Koike-Akino, D. Jha, B. Wang, C. Lin, K. Parsons. Deep neural network inverse design of integrated photonic power splitters. Sci. Rep., 9, 1368(2019).
[33] D. Dai, J. E. Bowers. Novel concept for ultracompact polarization splitter-rotator based on silicon nanowires. Opt. Express, 19, 10940-10949(2011).
[34] Y. Xiong, D.-X. Xu, J. H. Schmid, P. Cheben, S. Janz, W. N. Ye. Fabrication tolerant and broadband polarization splitter and rotator based on a taper-etched directional coupler. Opt. Express, 22, 17458-17465(2014).

Set citation alerts for the article
Please enter your email address



