- Photonics Research
- Vol. 9, Issue 7, 1204 (2021)
Abstract
1. INTRODUCTION
During the last decades, there has been an increasing interest in the study of structured light and associated optical beam shaping techniques [1,2]. Prior to this enthusiasm, optical vortex beams constituting the fundamental element of singular optics [3–5] have already attracted a great deal of attention due to the peculiar characteristics associated with their phase singularity, topological charge, and hollow intensity distribution [6–12]. Their ability to carry orbital angular momentum (OAM), transferrable to an illuminated object, along with a number of related properties has further paved the way toward novel opportunities for scientific research and advanced applications [7]. These include, for example, optical tweezers and spanners [8,9] and high-order quantum entanglement [10,11]. The hollow-core intensity shape allows to circumvent the particles being susceptible to elevated absorptive heating, due to the high-intensity peak located at the center of the fundamental Gaussian beam typically emitted by a standard laser. All these applications require a comprehensive understanding of the intensity distribution and OAM flux within optical vortices. In this regard, a larger variety of optical vortex structures have been reported in the literature [6,7]; some classical examples are optical Laguerre–Gaussian [13–15], high-order Bessel [16,17], helical Ince–Gaussian [18,19], and vector vortex [20,21] beams. Among them, high-order Bessel beams offer significant advantages with respect to other hollow beams because of their nondiffracting properties, which make them ideal for long-distance particle and atom transport [22]. It has also been shown that it is possible to generate high-order Bessel-like beams with the radius of the hollow core and maximum intensity fully controllable as a function of the propagation distance [23]. In general, diffraction is an undesired effect of light that causes beam expansion and peak intensity deterioration. A great amount of research efforts have been devoted in recent years to finding optical beams that are capable to counteract diffraction in different long-distance frameworks [24–27]. Although nondiffracting beams can be achieved via nonlinear effects forming spatial solitons [28–30] or via localized modes in photonic structures [31], the requirement of nonlinear media and/or complex structure design could hamper the applicability of such beams. In free space, the first introduction of optical Bessel beams [32,33] has stimulated the generation of a variety of light beams with propagation-invariant properties such as Mathieu [34,35] and Bessel-like [23,36–38] beams.
Since Airy wave packet was introduced to optics [2,39,40], the nondiffracting properties of the light have also been extended beyond a straight-line propagation into curved paths, where various families of self-accelerating beams that are mostly based on an Airy-like profile have been proposed and demonstrated [41,42]. Of particular interest is the class of so-called “abruptly autofocusing beams,” especially for potential uses in material ablation and medical surgery, driven by the fact that such radially symmetric self-accelerating beams can exhibit a low-intensity propagation combined with a controllable abrupt autofocusing right before a target [43–47]. Further research advances have also shown the possibility for the propagation of autofocusing vortex beams carrying OAM [48]. Due to their intrinsic characteristics, all these optical beams present significant diffraction and hence a rapid decrease in their peak intensities during subsequent propagation after the focal point. Applications exploiting the inherent properties of nondiffractive beams can benefit in many areas, including biomedical imaging, filamentation, particle manipulation, and free-space optical communications [2,49–55]. Ideally, every nondiffractive beam carries infinite power, thanks to which it can counteract diffraction indefinitely. Such a “perfect generation” with a stable amplitude profile over any propagation distance would require the illumination of an infinite transforming element with an ideal plane wave. Nevertheless, due to physical limitations present in all experimental settings, real beams must be truncated by an aperture and, as a consequence, diffraction takes place, resulting in antidiffracting beams with propagation distances extending from only a few centimeters to meters. (Note that the term “antidiffracting beam” is now widely used to refer to an arbitrary structured light that is capable of counteracting diffraction for a certain range of distances, although it is not “diffraction-free” in a strict sense. Such a mixed use of terms can be confusing because antidiffracting could be associated with a special propagation regime [56] such as free-scale dynamics achieved in a particular type of nonlinear media [57–59].)
Recently, a new class of antidiffracting light waves, named “optical pin beams” (OPBs), has been demonstrated, showing a robust propagation through atmosphere turbulence over distances of kilometers when compared to a standard Gaussian beam [27]. Further research advances have also generalized the class of OPBs and demonstrated their robustness and intensity stability even in a strong scattering medium [60], with a better performance when compared with other nondiffracting beams such as abruptly autofocusing [43,45,46] and Bessel-type [32] beams.
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
In this paper, we report the first experimental demonstration of long-distance generation of pin-like optical vortex beams (POVBs) in free space, representing a topological extension of the previously introduced OPBs [27,60]. We analyze the existence of such POVBs. Compared to previous works based on fundamental Bessel configurations, the POVBs exhibit an initial autofocusing stage followed by an amplitude reshaping into a high-order Bessel-like beam, however, the hollow-core radius and the annular main-lobe width vary with the propagation distance. Interestingly, the peak intensity evolution can be easily controlled by imposing a properly designed amplitude modulation. POVBs are investigated not only from the viewpoint of their propagation properties, where several examples are numerically and experimentally illustrated, but also from their energy characteristics through calculating the associated Poynting vectors and optical forces.
2. THEORY
The analysis starts by introducing the vector potential of an arbitrary optical beam,
3. EXPERIMENTAL DEMONSTRATION
We have experimentally observed the POVBs described theoretically in the previous section. In our experimental setup, as illustrated in Fig. 1(a), a phase-only spatial light modulator (SLM), i.e., a liquid crystal device (Holoeye PLUTO-VIS-016, 8-bit gray phase levels,
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
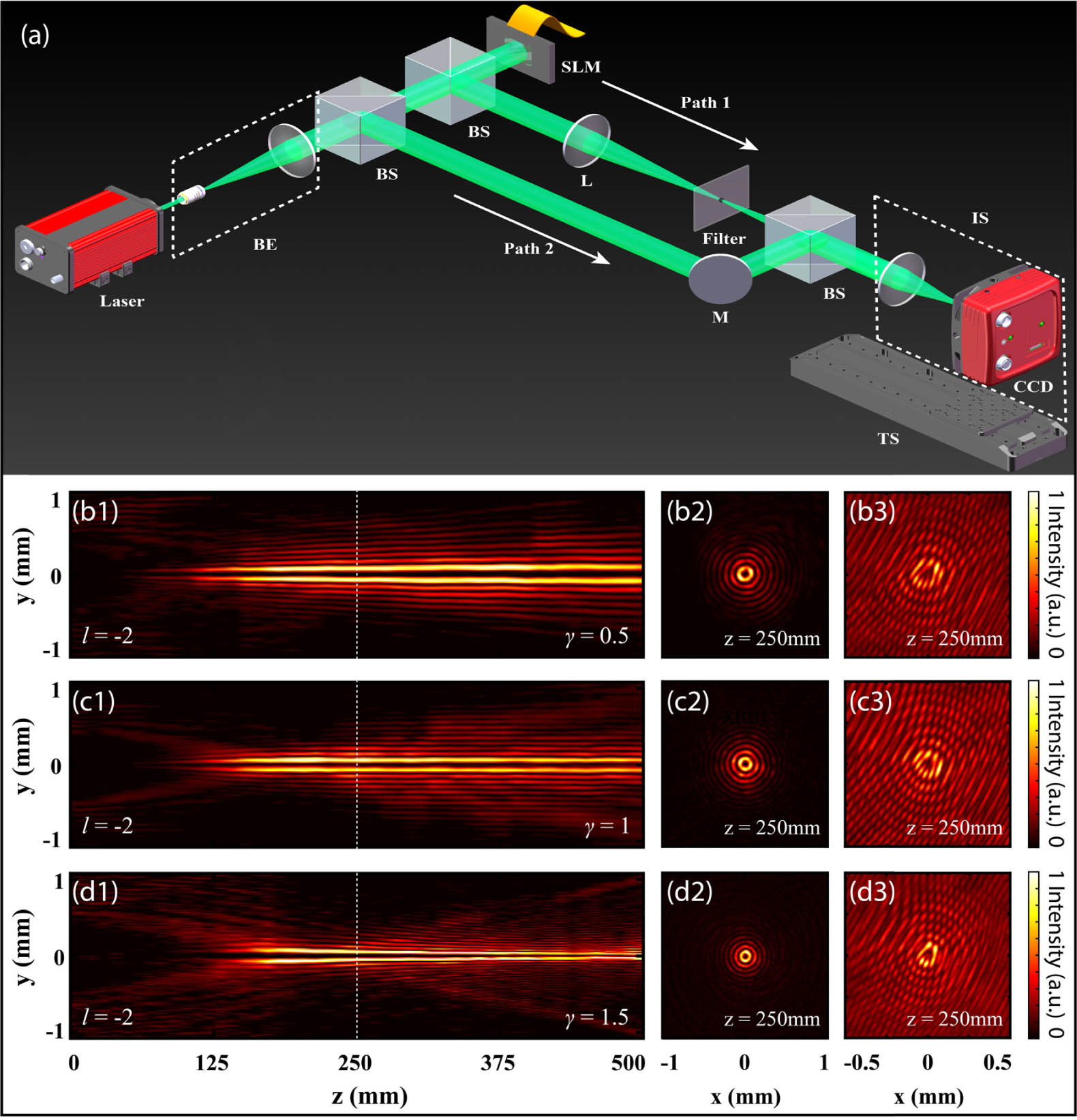
Figure 1.Experimental observations of POVBs in free space for different values of the phase modulation exponent
Figures 1(b1)–1(d3) present experimental results associated with three different cases of POVBs, where the power-law phase exponent coefficient
![]()
Figure 2.Numerical simulation of POVBs for different values of the parameter
![]()
Figure 3.Numerical (left) and experimental (right) results of POVBs in free space with
4. NUMERICAL SIMULATIONS
The above experimental observations can be corroborated with numerical simulations. To this purpose, Fig. 2 presents numerical results for the three cases corresponding to the measurements illustrated in Fig. 1. In particular, computations are carried out by solving Eq. (1) via the split-step Fourier transform method. All values of the parameters used in simulations are consistent with physical dimensions in our experimental setting. For the sake of completeness, we also list the other parameters used in our simulations:
![]()
Figure 4.Numerical calculations of Poynting vectors associated to the POVBs with topological charge
5. CONTROL OF THE PEAK INTENSITY EVOLUTION
So far, the discussion has been only restricted to the PVOBs that display a constant or low-varying peak intensity evolution during subsequent propagation after initial autofocusing. Now we explore the tunability of the peak intensity over a long range of distances by properly engineering the initial amplitude modulation
Analytical Peak Intensity of the POVBs in Fig.
| POVBs | Analytical Peak Intensity versus z |
|---|---|
| Steady state | |
| Hyperbolic secant | |
| Flat-top | |
| Sinusoidal |
6. POYNTING VECTORS AND OPTICAL FORCES
As seen above, the POVBs can be designed to exhibit tunable features, with either a constant or a pin-like vortex core as well as a controllable peak intensity evolution, in addition to preserved OAM during propagation. Besides the propagation properties, for both fundamental understanding and applications, it is also useful to investigate the energy-linked features associated with this class of optical beams. In this section, two key quantities related to the electromagnetic energy carried by POVBs are numerically explored: the Poynting vectors and the optical forces.
A. Poynting Vectors of POVBs
The Poynting vector represents the energy flux of the radiation field per unit area and is defined as
Numerically calculated Poynting vectors of the POVBs from Eq. (7) are illustrated in Figs. 4(a1)–4(a5) and 4(b1)–4(b5) at selected distances for two different values of
B. Optical Forces of POVBs
Optical forces originate from the transfer of linear or angular momentum from an optical beam to an illuminated object, essential for optical trapping and manipulation. As an illustrative example, we study here the optical forces exerted by a linearly polarized POVB on a spherical dielectric nanoparticle, suspended in a medium with a dielectric constant
7. CONCLUSION
In this work, we have experimentally demonstrated pin-like optical vortex beams and investigated their energy flow properties by numerically calculating the Poynting vectors and the optical radiation forces. These vortex beams are generated by modulating both the amplitude and the phase profile of an input laser beam through a spatial phase structure composed of a radially symmetric power-law phase chirp profile and an OAM phase term with an arbitrary topological charge. A POVB initially exhibits an autofocusing evolution and reaches the maximum intensity, and then it displays a reshaping of the amplitude pattern into a high-order Bessel-like beam whose annular main-lobe width and hollow-core radius change during propagation. An appropriate design of the initial amplitude based on the theoretical analysis allows control of the beam peak intensity along with the propagation range. Moreover, we have also shown that the transverse power flux initially flows radially from the beam sub-lobes toward the beam center to form the vortex structure and then localizes and rotates with the higher values of the Poynting vectors concentrated in the main lobe of the annular beam. Finally, we have studied the optical radiation forces associated with these vortex pins and shown their dependence on the design parameters for the POVBs. These specially designed beams can lead to optimal optical forces for trapping and manipulating a nanoparticle under test. Moreover, this research expands the understanding of free-space generation of antidiffracting optical vortex beams and builds up a connection between singular optics and structured light, which may find applications in different areas such as optical communication and quantum information technologies.
Acknowledgment
Acknowledgment. We thank Ze Zhang for assistance. R.M. is affiliated with UESTC as an adjoining faculty.
References
[1] H. Rubinsztein-Dunlop, A. Forbes, M. V. Berry, M. R. Dennis, D. L. Andrews, M. Mansuripur, C. Denz, C. Alpmann, P. Banzer, T. Bauer, E. Karimi, L. Marrucci, M. Padgett, M. Ritsch-Marte, N. M. Litchinitser, N. P. Bigelow, C. Rosales-Guzmán, A. Belmonte, J. P. Torres, T. W. Neely, M. Baker, R. Gordon, A. B. Stilgoe, J. Romero, A. G. White, R. Fickler, A. E. Willner, G. Xie, B. McMorran, A. M. Weiner. Roadmap on structured light. J. Opt., 19, 013001(2017).
[2] N. K. Efremidis, Z. Chen, M. Segev, D. N. Christodoulides. Airy beams and accelerating waves: an overview of recent advances. Optica, 6, 686-701(2019).
[3] M. S. Soskin, M. V. Vasnetsov. Singular optics. Prog. Opt., 42, 219-276(2001).
[4] A. S. Desyatnikov, L. Torner, Y. S. Kivshar. Optical vortices and vortex solitons. Prog. Opt., 47, 291-391(2005).
[5] M. R. Dennis, K. O’Holleran, M. J. Padgett. Singular optics: optical vortices and polarization singularities. Prog. Opt., 53, 293-363(2009).
[6] J. E. Curtis, D. G. Grier. Structure of optical vortices. Phys. Rev. Lett., 90, 133901(2003).
[7] Y. Shen, X. Wang, Z. Xie, C. Min, X. Fu, Q. Liu, M. Gong, X. Yuan. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl., 8, 90(2019).
[8] N. B. Simpson, L. Allen, M. J. Padgett. Optical tweezers and optical spanners with Laguerre–Gaussian modes. J. Mod. Opt., 43, 2485-2491(1996).
[9] H. He, M. E. Friese, N. R. Heckenberg, H. Rubinsztein-Dunlop. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett., 75, 826-829(1995).
[10] T. Stav, A. Faerman, E. Maguid, D. Oren, V. Kleiner, E. Hasman, M. Segev. Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science, 361, 1101-1104(2018).
[11] R. Fickler, G. Campbell, B. Buchler, P. K. Lam, A. Zeilinger. Quantum entanglement of angular momentum states with quantum numbers up to 10,010. Proc. Natl. Acad. Sci. USA, 113, 13642-13647(2016).
[12] K. T. Gahagan, G. A. Swartzlander. Optical vortex trapping of particles. Opt. Lett., 21, 827-829(1996).
[13] L. Allen, M. W. Beijersbergen, R. J. Spreeuw, J. P. Woerdman. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A, 45, 8185-8189(1992).
[14] F. Flossmann, U. T. Schwarz, M. Maier. Propagation dynamics of optical vortices in Laguerre–Gaussian beams. Opt. Commun., 250, 218-230(2005).
[15] Y. Cai, X. Lu, Q. Lin. Hollow Gaussian beams and their propagation properties. Opt. Lett., 28, 1084-1086(2003).
[16] J. Arlt, K. Dholakia. Generation of high-order Bessel beams by use of an axicon. Opt. Commun., 177, 297-301(2000).
[17] K. Volke-Sepulveda, V. Garcés-Chávez, S. Chávez-Cerda, J. Arlt, K. Dholakia. Orbital angular momentum of a high-order Bessel light beam. J. Opt. B, 4, S82-S89(2002).
[18] S. Chávez-Cerda, M. J. Padgett, I. Allison, G. H. C. New, J. C. Gutiérrez-Vega, A. T. O’Neil, I. MacVicar, J. Courtial. Holographic generation and orbital angular momentum of high-order Mathieu beams. J. Opt. B, 4, S52-S57(2002).
[19] C. Lopez-Mariscal, J. C. Gutierrez-Vega, G. Milne, K. Dholakia. Orbital angular momentum transfer in helical Mathieu beams. Opt. Express, 14, 4182-4187(2006).
[20] Y. F. Chen, T. H. Lu, K. F. Huang. Observation of spatially coherent polarization vector fields and visualization of vector singularities. Phys. Rev. Lett., 96, 033901(2006).
[21] C. Rosales-Guzmán, B. Ndagano, A. Forbes. A review of complex vector light fields and their applications. J. Opt., 20, 123001(2018).
[22] J. Arlt, T. Hitomi, K. Dholakia. Atom guiding along Laguerre-Gaussian and Bessel light beams. Appl. Phys. B, 71, 549-554(2000).
[23] M. Goutsoulas, D. Bongiovanni, D. Li, Z. Chen, N. K. Efremidis. Tunable self-similar Bessel-like beams of arbitrary order. Opt. Lett., 45, 1830-1833(2020).
[24] R. Grunwald, M. Bock. Needle beams: a review. Adv. Phys. X, 5, 1736950(2020).
[25] X. Weng, Q. Song, X. Li, X. Gao, H. Guo, J. Qu, S. Zhuang. Free-space creation of ultralong anti-diffracting beam with multiple energy oscillations adjusted using optical pen. Nat. Commun., 9, 5035(2018).
[26] C. Vetter, R. Steinkopf, K. Bergner, M. Ornigotti, S. Nolte, H. Gross, A. Szameit. Realization of free-space long-distance self-healing Bessel beams. Laser Photon. Rev., 13, 1900103(2019).
[27] Z. Zhang, X. Liang, M. Goutsoulas, D. Li, X. Yang, S. Yin, J. Xu, D. N. Christodoulides, N. K. Efremidis, Z. Chen. Robust propagation of pin-like optical beam through atmospheric turbulence. APL Photon., 4, 076103(2019).
[28] Z. Chen, M. Segev, D. N. Christodoulides. Optical spatial solitons: historical overview and recent advances. Rep. Prog. Phys., 75, 086401(2012).
[29] Y. V. Kartashov, B. A. Malomed, L. Torner. Solitons in nonlinear lattices. Rev. Mod. Phys., 83, 247-305(2011).
[30] R. Gautam, A. Bezryadina, Y. Xiang, T. Hansson, Y. Liang, G. Liang, J. Lamstein, N. Perez, B. Wetzel, R. Morandotti, Z. Chen. Nonlinear optical response and self-trapping of light in biological suspensions. Adv. Phys. X, 5, 1778526(2020).
[31] L. Tang, D. Song, S. Xia, S. Xia, J. Ma, W. Yan, Y. Hu, J. Xu, D. Leykam, Z. Chen. Photonic flat-band lattices and unconventional light localization. Nanophotonics, 9, 1161-1176(2020).
[32] J. Durnin, J. J. Miceli, J. H. Eberly. Diffraction-free beams. Phys. Rev. Lett., 58, 1499-1501(1987).
[33] J. Durnin. Exact solutions for nondiffracting beams. I. The scalar theory. J. Opt. Soc. Am. A, 4, 651-654(1987).
[34] J. C. Gutierrez-Vega, M. D. Iturbe-Castillo, S. Chavez-Cerda. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett., 25, 1493-1495(2000).
[35] P. Zhang, Y. Hu, T. Li, D. Cannan, X. Yin, R. Morandotti, Z. Chen, X. Zhang. Nonparaxial Mathieu and Weber accelerating beams. Phys. Rev. Lett., 109, 193901(2012).
[36] I. D. Chremmos, Z. Chen, D. N. Christodoulides, N. K. Efremidis. Bessel-like optical beams with arbitrary trajectories. Opt. Lett., 37, 5003-5005(2012).
[37] J. Zhao, P. Zhang, D. Deng, J. Liu, Y. Gao, I. D. Chremmos, N. K. Efremidis, D. N. Christodoulides, Z. Chen. Observation of self-accelerating Bessel-like optical beams along arbitrary trajectories. Opt. Lett., 38, 498-500(2013).
[38] M. Goutsoulas, N. K. Efremidis. Precise amplitude, trajectory, and beam-width control of accelerating and abruptly autofocusing beams. Phys. Rev. A, 97, 063831(2018).
[39] G. A. Siviloglou, D. N. Christodoulides. Accelerating finite energy Airy beams. Opt. Lett., 32, 979-981(2007).
[40] G. A. Siviloglou, J. Broky, A. Dogariu, D. N. Christodoulides. Observation of accelerating Airy beams. Phys. Rev. Lett., 99, 213901(2007).
[41] M. A. Bandres. Accelerating beams. Opt. Lett., 34, 3791-3793(2009).
[42] M. A. Bandres. Accelerating parabolic beams. Opt. Lett., 33, 1678-1680(2008).
[43] N. K. Efremidis, D. N. Christodoulides. Abruptly autofocusing waves. Opt. Lett., 35, 4045-4047(2010).
[44] P. Zhang, J. Prakash, Z. Zhang, M. S. Mills, N. K. Efremidis, D. N. Christodoulides, Z. Chen. Trapping and guiding microparticles with morphing autofocusing Airy beams. Opt. Lett., 36, 2883-2885(2011).
[45] D. G. Papazoglou, N. K. Efremidis, D. N. Christodoulides, S. Tzortzakis. Observation of abruptly autofocusing waves. Opt. Lett., 36, 1842-1844(2011).
[46] I. Chremmos, N. K. Efremidis, D. N. Christodoulides. Pre-engineered abruptly autofocusing beams. Opt. Lett., 36, 1890-1892(2011).
[47] S. N. Khonina, A. P. Porfirev, A. V. Ustinov. Sudden autofocusing of superlinear chirp beams. J. Opt., 20, 025605(2018).
[48] B. Chen, C. Chen, X. Peng, Y. Peng, M. Zhou, D. Deng. Propagation of sharply autofocused ring Airy Gaussian vortex beams. Opt. Express, 23, 19288-19298(2015).
[49] F. O. Fahrbach, P. Simon, A. Rohrbach. Microscopy with self-reconstructing beams. Nat. Photonics, 4, 780-785(2010).
[50] T. Vettenburg, H. I. Dalgarno, J. Nylk, C. Coll-Llado, D. E. Ferrier, T. Cizmar, F. J. Gunn-Moore, K. Dholakia. Light-sheet microscopy using an Airy beam. Nat. Methods, 11, 541-544(2014).
[51] S. Jia, J. C. Vaughan, X. Zhuang. Isotropic 3D super-resolution imaging with a self-bending point spread function. Nat. Photonics, 8, 302-306(2014).
[52] P. Polynkin, M. Kolesik, J. V. Moloney, G. A. Siviloglou, D. N. Christodoulides. Curved plasma channel generation using ultraintense Airy beams. Science, 324, 229-232(2009).
[53] J. Baumgartl, M. Mazilu, K. Dholakia. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics, 2, 675-678(2008).
[54] S. Chen, S. Li, Y. Zhao, J. Liu, L. Zhu, A. Wang, J. Du, L. Shen, J. Wang. Demonstration of 20-Gbit/s high-speed Bessel beam encoding/decoding link with adaptive turbulence compensation. Opt. Lett., 41, 4680-4683(2016).
[55] N. Ahmed, Z. Zhao, L. Li, H. Huang, M. P. Lavery, P. Liao, Y. Yan, Z. Wang, G. Xie, Y. Ren, A. Almaiman, A. J. Willner, S. Ashrafi, A. F. Molisch, M. Tur, A. E. Willner. Mode-division-multiplexing of multiple Bessel-Gaussian beams carrying orbital-angular-momentum for obstruction-tolerant free-space optical and millimetre-wave communication links. Sci. Rep., 6, 22082(2016).
[56] E. DelRe, A. J. Agranat, C. Conti. Light with no spatial scale: diffraction cancellation, anti-diffraction, scale-free instability and subwavelength beam propagation in dipolar glasses. Advanced Photonics Congress, NW3D.1(2012).
[57] E. DelRe, E. Spinozzi, A. J. Agranat, C. Conti. Scale-free optics and diffractionless waves in nanodisordered ferroelectrics. Nat. Photonics, 5, 39-42(2010).
[58] E. DelRe, F. Di Mei, J. Parravicini, G. Parravicini, A. J. Agranat, C. Conti. Subwavelength anti-diffracting beams propagating over more than 1,000 Rayleigh lengths. Nat. Photonics, 9, 228-232(2015).
[59] H. Harutyunyan. Anti-diffraction of light. Nat. Photonics, 9, 213-214(2015).
[60] D. Li, D. Bongiovanni, M. Goutsoulas, S. Xia, Z. Zhang, Y. Hu, D. Song, R. Morandotti, N. K. Efremidis, Z. Chen. Direct comparison of anti-diffracting optical pin beams and abruptly autofocusing beams. OSA Continuum, 3, 1525-1535(2020).
[61] J. A. Davis, D. M. Cottrell, J. Campos, M. J. Yzuel, I. Moreno. Encoding amplitude information onto phase-only filters. Appl. Opt., 38, 5004-5013(1999).
[62] L. Allen, M. J. Padgett, M. Babiker. The orbital angular momentum of light. Prog. Opt., 39, 291-372(1999).
[63] G. Chen, X. Huang, C. Xu, L. Huang, J. Xie, D. Deng. Propagation properties of autofocusing off-axis hollow vortex Gaussian beams in free space. Opt. Express, 27, 6357-6369(2019).
[64] Y. Harada, T. Asakura. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun., 124, 529-541(1996).
[65] Y. Roichman, B. Sun, Y. Roichman, J. Amato-Grill, D. G. Grier. Optical forces arising from phase gradients. Phys. Rev. Lett., 100, 013602(2008).
[66] J. Zhao, I. D. Chremmos, D. Song, D. N. Christodoulides, N. K. Efremidis, Z. Chen. Curved singular beams for three-dimensional particle manipulation. Sci. Rep., 5, 12086(2015).

Set citation alerts for the article
Please enter your email address



