Valeria Cimini, Mauro Valeri, Emanuele Polino, Simone Piacentini, Francesco Ceccarelli, Giacomo Corrielli, Nicolò Spagnolo, Roberto Osellame, Fabio Sciarrino. Deep reinforcement learning for quantum multiparameter estimation[J]. Advanced Photonics, 2023, 5(1): 016005
Search by keywords or author
- Advanced Photonics
- Vol. 5, Issue 1, 016005 (2023)
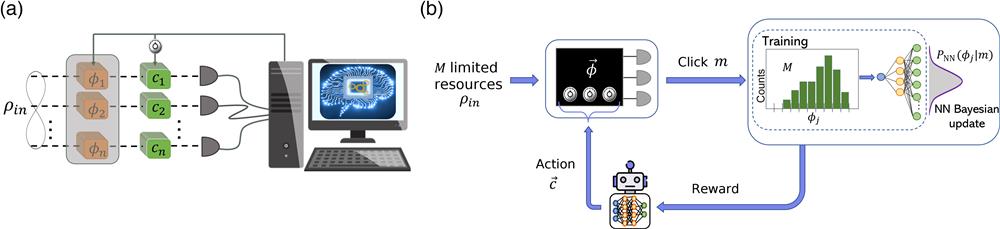
Fig. 1. (a) Generic multiparameter estimation problem fully managed by artificial intelligence processes. Quantum probes evolve through the investigated system and consequently their state changes depending on
![Single-phase estimation in a Mach–Zehnder interferometer. (a) Averaged quadratic loss as a function of the number of probes N, computed over 30 repetitions of 100 phase values of φ∈[0,π]. The results are obtained setting the control phase to zero. We compare the results obtained when having the full knowledge of the outcome probabilities (green line), with the ones achieved using the NN-reconstructed single-measurement posterior probability (blue line) and the ones resulting from approximating the lHd of the system with the occurence frequencies (yellow line), both retrieved performing r=10 measurements for each of the Nφ=100 grid points. In the inset, we report the ratio among the average Qloss achieved with the NN and the one retrieved using the lHd for ideal (blue) and noisy (purple) conditions. We compare the results with V=0.8, changing the number of measurements r in the training set. (b) lHd functions relative to the two possible measurements outcomes reconstructed via the NN on the left and with the standard calibration procedure on the right with r=10 and Nφ=100 in the π interval. The continuous lines represent P(d|φ), for d=0 (blue) and d=1 (red). (c) Averaged quadratic loss, as a function of the number of probes N, computed over 30 repetitions of 100 phase values of φ∈[ϵ,2π−ϵ]. Results obtained with the lHd and the NN update (reported in green and blue, respectively) when estimating φ∈[ϵ,π−ϵ] without feedbacks (light green and light blue lines) and applying random feedback after each probe (green and blue lines). The shaded area in the plots represents the interval of one standard deviation, whereas the dashed black line is the SNL=1/N. (d) lHd functions relative to the two possible measurements outcomes reconstructed via the NN obtained for r=1000 and Nφ=200 in the 2π interval, for d=0 (blue) and d=1 (red). On the right is reported the posterior NN probability reconstructed after 20 probe states were measured. As discussed in the main text, due to the nonmonotoncity of the output probabilities in the considered phase interval, the posterior shows two peaks, and this makes it necessary to use different feedback. The black line represents the true value of φ.](/richHtml/ap/2023/5/1/016005/img_002.png)
Fig. 2. Single-phase estimation in a Mach–Zehnder interferometer. (a) Averaged quadratic loss as a function of the number of probes
Fig. 3. Scheme of the integrated photonic phase sensor. The device consists in a four-arm interferometer with the possibility of estimating three optical phases adjusting three relative phase feedbacks through thermo-optic effects. Two-photon states are injected at the device input and both the Bayesian update and the choice of the optimal feedback are done through ML-based protocols trained directly on measurement outcomes.
Fig. 4. Experimental posterior probability distributions reconstructed by the NN. The points on the three axes correspond to the
Fig. 5. Estimate of
Fig. 6. Three-phase estimation in a four-arm interferometer. Achieved Qlosses [Eq. (10)] averaged over 100 different triplets of phases in the interval

Set citation alerts for the article
Please enter your email address



