Nonlinear localization of ultracold atomic Fermi gas in moir&#233; optical lattices

Xiuye Liu; Jianhua Zeng

doi:10.1117/1.APN.3.3.036006

Abstract

Moiré superlattices, a twisted functional structure crossing the periodic and nonperiodic potentials, have recently attracted great interest in multidisciplinary fields, including optics and ultracold atoms, because of their unique band structures, physical properties, and potential implications. Driven by recent experiments on quantum phenomena of bosonic gases, the atomic Bose–Einstein condensates in moiré optical lattices, by which other quantum gases such as ultracold fermionic atoms are trapped, could be readily achieved in ultracold atom laboratories, whereas the associated nonlinear localization mechanism remains unexploited. Here, we report the nonlinear localization theory of ultracold atomic Fermi gases in two-dimensional moiré optical lattices. The linear Bloch-wave spectrum of such a twisted structure exhibits rich nontrivial flat bands, which are separated by different finite bandgaps wherein the existence, properties, and dynamics of localized superfluid Fermi gas structures of two types, gap solitons and gap vortices (topological modes) with vortex charge S = 1, are studied numerically. Our results demonstrate the wide stability regions and robustness of these localized structures, opening up a new avenue for studying soliton physics and moiré physics in ultracold atoms beyond bosonic gases.

Keywords

density-functional equation gap solitons moiré optical lattices ultracold Fermi gases

1 Introduction

Optical lattices, artificial periodic potentials generated by counterpropagating multiple laser beam interferences, are one of the enabled and particularly attractive transformative technologies for studying and controlling the nonlinear and quantum (many-body physics) properties of ultracold atomic gases.1^–3 Ultracold atoms such as Bose–Einstein condensates, loaded upon various kinds of optical lattices, have resulted in the discovery of novel physics and the creation of a great many emergent nonlinear phenomena such as diverse matter-wave solitons.4^–7 Deserved to be mentioned, localized gap modes in the forms of gap solitons and vortices can be launched and investigated in ultracold atoms (no matter Bose–Einstein condensates and degenerate Fermi gases or their coalition) trapped by optical lattices that own a forbidden atomic bandgap.8^–21

In condensed matter physics territory, a recently achieved major triumph was the observations of remarkable physical effects referring to unconventional superconducting under small magic twisted angles and strongly correlated insulating properties (to name a few) in two-dimensional (2D) twisted bilayer graphene, which belongs to a new 2D material called moiré superlattices consisting of a periodic structure overlapped with its copy but twisted in a certain angle.22^–26 Twistronics has thus emerged as an active research frontier in the past few years.27^–29 Stimulated by such a stream of research, revealing linear, nonlinear, and quantum physical peculiarities of light and matter waves in moiré patterns and transformational structures has recently been extended to the optics and photonics contexts.30^–44 Particularly, the linear localization of light and transition between localization and delocalization due to the unique flat-band property has been first confirmed in photonic moiré lattices;31 in such a setting but adding nonlinearity, an extremely low threshold of optical soliton formation via twisted angle was also observed experimentally by the same group.32 Other localization and quantum physics were also recently revealed in moiré structures of different kinds.33^–44

Very recently, new solitons physics and nonlinear localization mechanisms have been popping up in nonlinear optics and physics settings with moiré structures.33^,45^–50 These include, but are not limited to, the generation of multifrequency solitons in quadratic nonlinear media,45 light bullets,46 and vortex solitons47 as well as 2D Thouless pumping33 of light in photonic moiré lattices; linear and nonlinear light localizations at the edges of moiré arrays;48 2D gap solitons in parity-time symmetric and regular moiré optical lattices;49 matter-wave gap solitons; and vortices in dense Bose–Einstein condensates with moiré optical lattices.50 However, one can find that all these soliton studies are in the Boson settings;33^,45^–50 it is instructive to study soliton formations and disclose the nonlinear localization theory in other physical settings such as degenerate Fermi gases.

Sign up for Advanced Photonics Nexus TOC. Get the latest issue of Advanced Photonics Nexus delivered right to you！Sign up now

This work is intended to explore how the nonlinear localization of superfluid Fermi gases trapped by moiré optical lattices works and what kinds of robust localized gap modes can be created and how to launch them. By means of linear Bloch theory, we find that such 2D twisted bilayer optical lattices have abundant extremely flat bands and that the widths of numbered finite gaps vary differently with the change of twisted angle and strength contrast of the two sublattices. Our systematic numerical simulations and theoretical analysis demonstrate that the band flatness could enable us to construct robust 2D localized gap modes as fundamental gap solitons and vortices (with imprinted vorticity $S = 1$ ) inside the several finite gaps (whose first, second, third, fourth, and fifth finite gaps are examined). The robustness of both localized gap modes implies that the moiré optical lattices can be set as an ideal platform for predicting and observing emergent nonlinear wave structures in the settings of ultracold atomic gases with shallow (small strength) lattices, providing a new degree of freedom in exploring and tuning the nonlinear physics of ultracold atom settings with diverse gases. We would like to emphasize that while flat bands appear also in conventional optical lattices; the condition is that the optical lattices should be fabricated deep enough (very large lattice strength, hard to realize) or in special spatial configurations. The nonlinear localization physics revealed here is positive, timely, and meaningful, given the fact that the atomic Bose–Einstein condensate has recently been prepared in twisted bilayer optical lattices,51 and its Fermi counterpart (superfluid fermion gas in moiré optical lattices) can be readily implemented in the current state-of-the-art ultracold atomic laboratories.

2 Model and Its Linear Bloch Spectrum

2.1 Theoretical Model

Nonlinear evolutional dynamics of a 2D ultracold Fermi gas (Bardeen Cooper Schrieffer superfluid of spin-1/2 Fermionic atoms) loaded onto the moiré optical lattices in mean-field theory is governed by the density-functional equation (theory), whose scaled wave function (complex order parameter), $ψ$ , yields16^–18 $i \frac{\partial ψ}{\partial t} = - \frac{1}{2} \nabla^{2} ψ + V_{OL} (R) ψ + g | ψ |^{\frac{4}{3}} ψ,$ (1)where $R = (x, y)$ and Laplacian $\nabla^{2} = \partial^{2} / \partial x^{2} + \partial^{2} / \partial y^{2}$ , the nonlinear coefficient, $g$ , represent repulsive (self-defocusing) nonlinearity induced by atom–atom collisions, set as $g = 1$ (for discussion), which, in reality, can be tuned using the Feshbach resonance technology.52 It is relevant to remark that the nonlinearity represents a repulsive nonlinear term of power 7/3, which is unique for degenerate Fermi gases.

The 2D moiré optical lattices, consisting of two uniform square lattices with a twisted angle $θ$ to each other, follow $V_{OL} (R) = V_{1} (\cos^{2} x + \cos^{2} y) + V_{2} (\cos^{2} x^{'} + \cos^{2} y^{'}),$ (2)where $V_{1,2} > 0$ represents the modulation depth (amplitude) of the two optical lattices with periodicity $π$ . For convenient discussion, we take the strength difference as $P = V_{2} / V_{1}$ and set $V_{1} = 2$ and $V_{2} = 4$ throughout; otherwise it is highlighted. The transformation between the $(x, y)$ and $(x^{'}, y^{'})$ planes is, in mathematics and real spaces, defined by a rotating angle $θ$ : $\begin{matrix} (\begin{matrix} x^{'} \\ y^{'} \end{matrix}) = (\begin{matrix} \cos θ, - \sin θ \\ \sin θ, \cos θ \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) . \end{matrix}$ (3)

One can know from Eq. (2) that the moiré optical lattice returns to the normal square lattice if we set $V_{2} = 0$ or $θ = 0$ . The extraordinary feature of such a moiré pattern is that, when gradually changing the rotating angle $θ$ (between the two sublattices), the moiré optical lattice will be continuously transformed into the periodic and aperiodic structures, thereby filling a gap crossing of perfect periodic potentials and aperiodic structures and opening a new strategy for light-field manipulation (bandgap engineering) and its nonlinear dynamic control dependent merely on a new rotating degree of freedom of the sublattices even though under shallow lattice modulation. As pointed out in previous publications,30^–33^,44^,49^,50 such a moiré optical lattice allows the existence of the widest finite gaps separated by neighboring extremely flat Bloch bands provided that it is the perfect periodic pattern which, in fact, is achieved only if we consider the special case of Pythagorean angles $θ = \arctan (a / b)$ , with $\cos θ = a / c$ , $\sin θ = b / c$ , and natural numbers $(a, b, c)$ constitute Pythagorean triples, $a^{2} + b^{2} = c^{2}$ .

The stationary solitary matter-wave solution $ϕ$ under chemical potential $μ$ can be constructed as $ψ = ϕ e^{- i μ t}$ , and after substituting it into the dynamical fundamental equation [Eq. (1)], one can get the stationary equation, $μ ϕ = - \frac{1}{2} \nabla^{2} ϕ + V_{OL} (R) ϕ + | ϕ |^{\frac{4}{3}} ϕ .$ (4)

Equation (4) holds the norm (number of atoms) $N = \iint | ϕ |^{2} d x d y$ .

2.2 Linear Bandgap Properties

Although the fact that the moiré patterns could be twisted with arbitrary angles $θ$ , allowing ample band diagrams to emerge accordingly, the Pythagorean lattices (the moiré optical lattice under the unique case of Pythagorean angles $θ$ , as stressed above) support the optimal bandgap tuning, which is the spatial tailoring of the largest width of the finite gaps, within which the localized gap modes of diverse types to be excited are of our fundamental interest. Our attention here is only paid to the moiré optical lattices at different Pythagorean twisted angles $θ$ , which, in fact, are equipped with periodic translational symmetry, and therefore, the general linear Bloch bandgap theory widely used in solid-state physics and other periodic potentials, including photonic crystals and optical lattices, can be readily applied here. Bearing this in mind, one can produce the underlying linear Bloch spectrum after a routine operation.

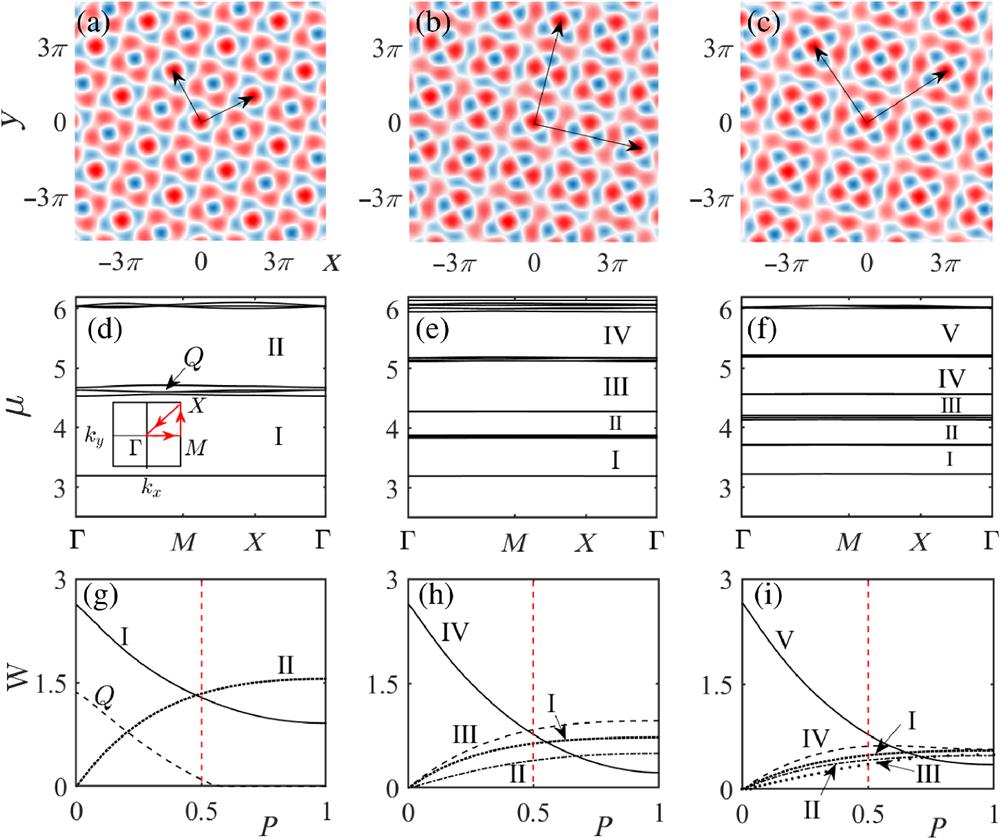
Contour profiles of Pythagorean moiré optical lattices under three different Pythagorean twisted angles $θ = \arctan (3 / 4)$ , $θ = \arctan (5 / 12)$ , and $θ = \arctan (8 / 15)$ are depicted in Figs. 1(a)–1(c), respectively. The three twisted angles enlarge the lattice period of moiré optical lattices as compared with the original square lattices ( $ε_{2} = 0$ or $θ = 0$ ). Ignoring the last nonlinear term of Eq. (4), calculating the corresponding eigenvalues within the first Brillouin zone in the reciprocal space [which is depicted in the inset of Fig. 1(d)], one can get the linear Bloch spectrum under the same strength difference $P = 0.5$ , as displayed separately in Figs. 1(d)–1(f) and in the bottom line of the figure with red dashed vertical lines. Once again, we can see that, as those discovered in other Pythagorean moiré lattices, despite being shallow, there are abundant flat Bloch bands for the Pythagorean moiré optical lattices; strikingly, the former features a very narrow gap (which we name minigap “ $Q$ ”) between the first and second gaps; the latter two cases exhibit more flat bands, and the higher finite gaps can be wider than their first one. Further research revealed that, for the former case, the widths of both the first gap and minigap decrease when increasing $P$ , and the minigap ( $Q$ ) disappears at $P > 0.53$ , while the second gap’s width grows gradually [Fig. 1(g)]; by comparison, the first gap’s width increases, whereas the decrease is only for the fourth and fifth gaps for the latter two cases, according to Figs. 1(h) and 1(i). These rich linear bandgap properties of moiré optical lattices indicate that very flexible and tunable bandgap engineering can be achieved by simply changing the rotating angle $θ$ and strength difference $P$ , providing a new linear (flat-band) localization mechanism (different from that of Anderson localization) of optical and matter waves,31 and robust nonlinear localization of various localized gap modes within those numbered finite gaps of the associated linear Bloch spectra, as will be presented below.

Figure 1.Linear Bloch-wave band structures of 2D moiré square optical lattices. The geometries, reduced Brillouin zone, and bandgap spectra of the 2D moiré square optical lattices under different Pythagorean twisted angles. Platforms of the moiré lattice (shaded red, lattice potential maxima; shaded blue, lattice potential minima) at different rotation angles: (a) $θ = \arctan (3 / 4)$ , (b) $θ = \arctan (5 / 12)$ , and (c) $θ = \arctan (8 / 15)$ , and the linear Bloch-wave spectrum (indicated as chemical potential $μ$ ) of the moiré lattice with different twisted angles: (d) $θ = \arctan (3 / 4)$ , (e) $θ = \arctan (5 / 12)$ , and (f) $θ = \arctan (8 / 15)$ ; subplot in panel (d) shows the first reduced Brillouin zone in the reciprocal space, where the associated high symmetry points are marked. The width of the finite gaps versus the relative strength of two layers of the lattice ( $P$ ) under different twisted angles: (g) $θ = \arctan (3 / 4)$ , (h) $θ = \arctan (5 / 12)$ , and (i) $θ = \arctan (8 / 15)$ . The second and third lines: the Roman numerals I, II, III, IV, and V are the first, second, third, fourth, and fifth finite gaps, respectively; $Q$ in panels (d) and (g) is the very narrow minigap. $P = 0.5$ for panels (a)–(f).

Before going further, let us introduce the numerical calculation recipes for launching the localized gap modes and testing their stability, which yield the following: the stationary solutions of the localized gap modes under consideration are first constructed through Eq. (4) using the widely used method—modified squared-operator iteration method;53 then, the stability and instability properties of the gap modes thus found will be scrutinized in direct perturbed numerical computation of the dynamical equation [Eq. (1)] by taking a converged and highly accurate computational approach called the fourth-order Runge–Kutta method.

3 Numerical Results and Discussions

3.1 Fundamental Gap Solitons

We first survey the excitation of the simplest matter-wave localized gap modes with a single peak and isotropic shapes called fundamental gap solitons, which can be upheld by the Pythagorean moiré optical lattices [Eq. (2)], as done in conventional periodic potentials. As far as the aforementioned three Pythagorean twisted angles [ $θ = \arctan (3 / 4)$ , $θ = \arctan (5 / 12)$ , and $θ = \arctan (8 / 15)$ ] are concerned, the corresponding relationships among the number of atoms, $N$ , and chemical potential $μ$ for the fundamental gap solitons are, respectively, depicted in Figs. 2(a)–2(c), showing a growing tendency through the first gap to the higher ones, and abiding by the well-known principle of the “anti-Vakhitov–Kolokolov” criterion, $d N / d μ > 0$ , an indispensable condition for the stable gap solitons under the regime of repulsive (defocusing) nonlinearity.6^,8^–15^,54 Detailed numerical perturbed calculations in the dynamics equation [Eq. (1)] reveal that these fundamental gap solitons are robustly stable localized modes existing in the middle of the finite gaps; they tend to be unstable near the edges of Bloch bands, as underlined in the figures. Moreover, we have examined the dependence between $N$ and the same sublattice depth $V_{0} = V_{1} = V_{2}$ , which is summed up in Fig. 2(d), demonstrating a decreasing trend with the increase of $V_{0}$ ; it coincides with the significant experimental finding of low threshold (of the laser power in nonlinear optics) for the formation of optical solitons in photonic moiré lattices. It is necessary to note that the typical profiles of the so-found fundamental gap solitons are shown in Figs. 2(e)–2(g), where the former is a stable gap soliton owning negligible side peaks, while the latter two are unstable ones accompanied by multiple side peaks that are induced by strong Bragg scattering. Such side peaks of the latter two solitons may cause instability in the course of time evolution.

Figure 2.Properties of fundamental gap solitons of ultracold Fermi gases controlled by moiré square optical lattices. Number of atoms, $N$ , versus chemical potential $μ$ (a)–(c), respectively, and the same sublattice depth ( $P = 1$ ) under $V_{0} = V_{1} = V_{2}$ (d) for the fundamental gap solitons, whose profiles for marked points ( $A$ , $B$ , and $C$ ) in panel (a) are shown in the third line, in 2D moiré square optical lattices at twisted angles: (a), (d) $θ = \arctan (3 / 4)$ , (b) $θ = \arctan (5 / 12)$ , and (c) $θ = \arctan (8 / 15)$ . Other parameters: (d) $μ = 4$ ; (e) $μ = 4$ , $N = 14.7$ ; (f) $μ = 4.7$ , $N = 36.8$ ; (g) $μ = 5.18$ , $N = 66.4$ . Here and below, red dashed lines in panels (a)–(c) represent unstable regions.

In the perturbed time evolution, as shown in Fig. 3, the stable fundamental gap soliton sustains its shape [Fig. 3(a)], while there are oscillating or growing side peaks (lobes) for the unstable fundamental modes [Figs. 3(b) and 3(c)]. Further insights into their evolutions confirm that the unstable fundamental gap solitons are only in the weakly unstable mode; this once again verifies the excellent platform for soliton formation and control in physical settings with moiré optical lattices.

Figure 3.Perturbed evolutions of fundamental gap solitons. Top-view profiles (a)–(c) and the perturbed evolution in real time (d)–(f) of typical fundamental gap solitons for the marked points ( $A$ , $B$ , and $C$ ) in Fig. 2(a): stable (a), weakly unstable (b), and strongly unstable (c) gap solitons.

3.2 Vortex Gap Solitons with Topological Charge $S = 1$

A more interesting thing is that whether such Pythagorean moiré optical lattices can give rise to robust vortex gap solitons and how to stabilize them at will. It is thus the target in this section to reveal these issues for gap vortices, the vortex gap solitons with topological charge $S$ ; for the sake of discussion, we only consider the case of $S = 1$ . As reported elsewhere, such gap vortices are usually featured by a null value in the middle and consist of four bright (fundamental gap solitons) modes/peaks that are entangled with $π / 2$ phase shifts between them, enabling the whole $2 π$ phase circulation ( $S = 1$ ). The stability regions of the gap vortices reduce a little bit compared with their fundamental gap solitons counterpart because of the existence of destructive interaction among the four solitons, as can be seen from the curve $N (μ)$ and the associated stability regions portrayed in Figs. 4(a)–4(c) for the three Pythagorean angles. Also, a decreasing relation $N (V_{0})$ proceeds for the vortex gap solitons, according to Fig. 4(d). The schematic shapes of the vortex gap solitons are displayed in Figs. 4(h)–4(j), the cross-sectional cut at $y = 1.5$ is displayed in Figs. 4(e)–4(g), and the associated spatial phase structures are depicted in the bottom line of Fig. 4 [see Figs. 4(k)–4(m)], showcasing the twisted modes unique for moiré lattices.

Figure 4.Properties of gap vortices of ultracold Fermi gases loaded upon moiré square optical lattices. Number of atoms, $N$ , versus chemical potential $μ$ (a)–(c) and the same sublattice depth ( $P = 1$ ) under $V_{0} = V_{1} = V_{2}$ (d) for the vortex gap solitons at topological charge $S = 1$ in 2D moiré square optical lattices at twisted angles: (a), (d) $θ = \arctan (3 / 4)$ , (b) $θ = \arctan (5 / 12)$ , and (c) $θ = \arctan (8 / 15)$ . Other parameters: (d) $μ = 4$ ; (e) $μ = 3.5$ , $N = 9.4$ ; (f) $μ = 4.6$ , $N = 120.5$ ; (g) $μ = 5.25$ , $N = 256.1$ . Red dashed lines in panels (a)–(c) represent unstable regions. The cross section (taken at $y = 1.5$ ), the associated profiles, and phase structures are depicted in the third, fourth, and fifth lines, respectively.

In direct perturbed simulations by solving the dynamical equation [Eq. (1)], we can see that the stable vortex gap soliton remains unchanged in long time evolution [Fig. 5(a)]; and for the unstable ones, as those displayed in Figs. 5(b) and 5(c), only their side peaks undergo regular oscillations and small strength growth, demonstrating weak instability.

Figure 5.Perturbed evolutions of gap vortices. Top-view profiles (a)–(c) and the perturbed evolution in real time (d)–(f) of typical vortex gap solitons for the marked points ( $D$ , $E$ , and $F$ ) in Fig. 4(a): stable (a), weakly unstable (b), and strongly unstable (c) gap vortices.

4 Conclusion and Discussion

In sum, we have presented numerical investigations and theoretical analysis of nonlinear localizations of 2D ultracold atomic Fermi gas in moiré optical lattices with repulsive (self-defocusing) nonlinearity. A noteworthy finding is that, although being formed in the systems with shallow optical lattices, the tightly localized gap modes, including fundamental gap solitons and vortices with topological charge $S = 1$ , laid inside the finite gaps spaced apart by extremely flat Bloch bands of the underlying linear Bloch spectrum, were shown to have strong localization and robust stability properties. Our nonlinear localization mechanism of ultracold atomic Fermi gas may be readily realized in ultracold atomic laboratories worldwide by means of a similar technique used in recently observed atomic Bose–Einstein condensate and quantum phase transition in 2D twisted bilayer optical lattices. We therefore expect the results predicted here to be of great interest in nonlinear sciences, since we suggest a new way for the creation and control of strongly localized matter-waves beyond atomic Bose–Einstein condensate in moiré optical lattices with shallow depth but exhibiting tunable flat bands and numbered finite gaps. Given the fact that the atomic Bose–Einstein condensate has recently been prepared in twisted bilayer optical lattices,51 its Fermi counterpart (superfluid fermionic gases in moiré optical lattices) can be readily implemented in the current state-of-the-art ultracold atomic laboratories.

Xiuye Liu is a postdoc at Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences. He received his PhD in optics from Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences in 2023. He is the author of more than 10 journal papers. His current research interests include optical solitons and ultracold atoms.

Jianhua Zeng is a professor and a PhD supervisor at Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Science. He has been an associate professor since July 2013. He obtained his PhD in 2010, jointly trained at Sun Yat-sen University (Guangzhou) and Weizmann Institute of Sciences, Israel, and then did two postdocs at Tel-Aviv University and Tsinghua University, Beijing. His research interests focus on theoretical nonlinear photonics, including nonlinear/ultrafast/quantum optics and ultracold quantum gases.

References

[1] E. Zohar, J. I. Cirac, B. Reznik. Quantum simulations of lattice gauge theories using ultracold atoms in optical lattices. Rep. Prog. Phys., 79, 014401(2015).

[2] C. Gross, I. Bloch. Quantum simulations with ultracold atoms in optical lattices. Science, 357, 995-1001(2017).

[3] F. Schäfer et al. Tools for quantum simulation with ultracold atoms in optical lattices. Nat. Rev. Phys., 2, 411-425(2020).

[4] O. Morsch, M. Oberthaler. Dynamics of Bose–Einstein condensates in optical lattices. Rev. Mod. Phys., 78, 179(2006).

[5] P. G. Kevrekidis, D. J. Frantzeskakis, R. Carretero-González. Emergent Nonlinear Phenomena in Bose–Einstein Condensates: Theory and Experiment, 45(2008).

[6] Y. V. Kartashov, B. A. Malomed, L. Torner. Solitons in nonlinear lattices. Rev. Mod. Phys., 83, 247(2011).

[7] Y. V. Kartashov et al. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys., 1, 185-197(2019).

[8] L. Zeng, J. Zeng. Gap-type dark localized modes in a Bose–Einstein condensate with optical lattices. Adv. Photonics, 1, 046004(2019).

[9] J.-C. Shi, J.-H. Zeng. Self-trapped spatially localized states in combined linear-nonlinear periodic potentials. Front. Phys., 15, 12602(2020).

[10] J. Li, J. Zeng. Dark matter-wave gap solitons in dense ultracold atoms trapped by a one-dimensional optical lattice. Phys. Rev. A, 103, 013320(2021).

[11] J. Chen, J. Zeng. Dark matter-wave gap solitons of Bose–Einstein condensates trapped in optical lattices with competing cubic-quintic nonlinearities. Chaos, Solitons Fractals, 150, 111149(2021).

[12] Z. Chen, J. Zeng. Localized gap modes of coherently trapped atoms in an optical lattice. Opt. Express, 29, 3011-3025(2021).

[13] Z. Chen, J. Zeng. Two-dimensional optical gap solitons and vortices in a coherent atomic ensemble loaded on optical lattices. Commun. Nonlinear Sci. Numer. Simul., 102, 105911(2021).

[14] X. Liu, B. A. Malomed, J. Zeng. Localized modes in nonlinear fractional systems with deep lattices. Adv. Theor. Simul., 5, 2100482(2022).

[15] Z. Chen, J. Zeng. Nonlinear localized modes in one-dimensional nanoscale dark-state optical lattices. Nanophotonics, 11, 3465-3474(2022).

[16] S. K. Adhikari, B. A. Malomed. Tightly bound gap solitons in a fermi gas. Europhys. Lett., 79, 50003(2007).

[17] S. K. Adhikari, B. A. Malomed. Gap solitons in a model of a superfluid fermion gas in optical lattices. Physica D, 238, 1402-1412(2009).