- High Power Laser Science and Engineering
- Vol. 9, Issue 2, 02000e28 (2021)
Abstract
1 Introduction
Conventionally, nonlinear media are employed to transform the fundamental frequency of the input laser to those of high harmonics to obtain extreme ultraviolet and even X-ray beams using table-top lasers[1,2]. High harmonic generation (HHG), as an ideal tool, can be applied in probing electronic dynamics on the atomic or molecular scale, microscale imaging, etc. Gases or metals are utilized to generate high-order harmonics for lasers with intensities around 1014–16 W/cm2[3–7], and a plasma target is ideal for lasers with much higher intensities, i.e., approximately or over 1018 W/cm2[8–15]. In general, all harmonics couple with the input laser(s), and they are not separated outside the interaction domain[16-20]; consequently, additional spectrometers are usually utilized to separate a specific-order harmonic for application[21-23]. Angular separation of high harmonics from solid plasma targets has been achieved experimentally in a single-beam scheme by using grating targets[24]. Enhancement of harmonics in the grating scheme via surface plasmon excitation has also been demonstrated[25]. On the other hand, angularly isolated high harmonics from a gas jet were first reportedly generated by two overlapping 1014 W/cm2 non-collinear laser beams[22]. This non-collinear HHG geometry presents numerous advantages[22,26-29], including the separation of the harmonics from the pump beams, angular separation of different order harmonics, generation of high-energy photons, and production of isolated attosecond bursts. Evidently, this HHG process meets the phase-matching requirement, which stipulates that the output momentum of an nth-order harmonic photon (kn) is only related to the momentum of the input photons (k1 and k2) by the momentum conservation principle, kn = n1k1 + n2k2, where n1 and n2 are the numbers of photons absorbed from each of the input beams, and n = n1 + n2[22,23,30]. As far as we know, all this interesting research is based on the gas ionization process, where the laser intensity is generally below 1016 W/cm2, and the crossing angle is small enough to ensure adequate interaction.
In this study, based on a different HHG mechanism, we propose an approach for generating intense isolated harmonics through the interaction between relativistic lasers and a plasma target, but with a quite different phase-matching selection rule. In our approach, two relativistic laser pulses impinge on a solid thin foil at an angle. The generated intense harmonics are naturally separated from each other and from the input beams at considerably large angles, which can be predicted. The proposed approach offers several exclusive benefits. First and most importantly, both our theoretical analysis and three-dimensional particle-in-cell (3D PIC) simulations prove that the nth harmonic carrying the information of both input lasers is converted by its adjacent (n – 1)th harmonic which has the smallest crossing angle with the nth harmonic owing to the highest occurrence possibility and one fundamental input beam, rather than directly by the two input beams in the gas HHG case. That is, considering phase matching, the output momentum (emission direction) of an nth-order harmonic photon depends on the momentum of the (n – 1)th-order harmonic photon and that of one input laser photon, according to the momentum conservation, kn = kn–1 + k1(2), for the input beams with the same wavelength. Second, plasma, as a nonlinear medium, can endure lasers nearly without the intensity limitation. Therefore, the intensity of isolated harmonics can be in the relativistic region[31,32]. Finally, because the crossing angle between the input lasers can be sufficiently large, the individual harmonic can be emitted at an angle nearly two orders of magnitude higher than that (usually in the milliradian level) in gas HHG. This point is very important for the measurement and application of this method in experiments. It should be noted that a large number of papers on the selection rule for the plasma HHG in terms of the oscillating mirror model, first proposed by Bulanov et al.[9] and then studied extensively by Lichters et al.[10], have been published. All of them are about a single incident laser or collinear incident lasers, and all of harmonics are coupled spatially. The problems such as proper phase matching do not exist. However, in our case, the harmonic emission is determined by the phase-matching relation and hence isolated angularly.
2 Theoretical analysis
The proposed scheme is shown in Figure 1. Two circularly polarized (CP) laser pulses a1 and a2 impinge on a solid thin foil symmetrically at a large crossing angle 2θ. For simplification, two identical input pulses with the same frequency (ω) are considered, and the angle θ = π/4 is the incident angle of each laser pulse. The electrons in the target experience the overlapped fields in the thin foil and oscillate. The harmonics radiated from the oscillating electrons are isolated angularly and propagate in the reflected side and also in the transmitted side if the target is sufficiently thin. The total normalized laser amplitude acting on the target is a = a1+a2 (
Sign up for High Power Laser Science and Engineering TOC. Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
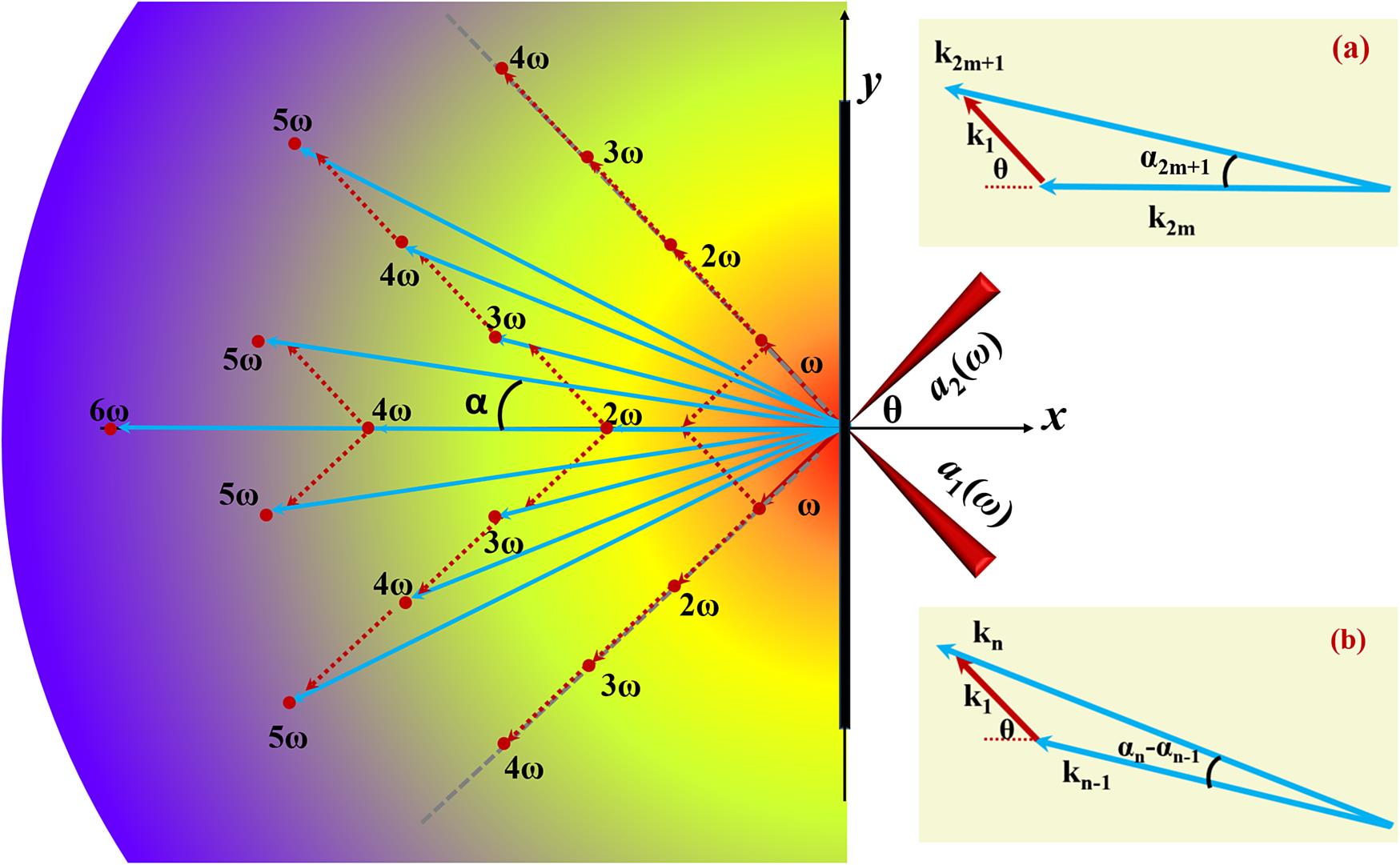
Figure 1.Schematic of the chain selection rule for the proposed approach. Two laser pulses
As an example, we adopt the z component of the input fields,
3 3D PIC simulations
The PIC simulation configuration is shown in Figure 2(a). The simulations are carried out using the EPOCH code[35]. Two CP laser pulses, a1 and a2, with the same frequency ω (the corresponding wavelength λ=1 μm) reach the target at the same angle θ=π/4 symmetrically. A peak normalized amplitude (a0) of 3 and a focal spot size of 5 μm are used. The laser profile is
![]()
Figure 2.(a) Configuration of the PIC simulation box. The input laser field distribution before the lasers strike the target. (b) Electric field ( (3.2×1012 V/m).
(3.2×1012 V/m).
Figure 3 shows the spectrum distribution of the harmonics in k-space after the Fourier transformation of the reflected electric field, Ez, in Figure 2(b). As expected, the harmonics include odd and even orders in the reflected directions. The harmonic locations marked with the small white circles in Figure 3 are obtained from Equation (4), showing the good agreement with the simulation results. Harmonics such as 2ω20, 3ω30, 4ω40, 2ω02, 3ω03, and 4ω04 only contain the information of one input laser pulse and propagate along the incident directions. Here we focus on the harmonics containing the information of both input laser pulses. They are generated and angularly isolated, including 2ω11 of the second harmonic, 3ω21 and 3ω12 of the third harmonics, and 4ω22, 4ω31, and 4ω13 of the fourth harmonics, as shown in Figure 3. The propagating directions of these harmonics are determined by vector addition according to their generation way, in which the phase-matching rule should be satisfied.
For example, there are four ways to generate the third harmonics in the photon picture according to energy conservation, i.e., 3ω=3×1ω (a1), 3ω=3×1ω (a2), 3ω=2ω+1ω (a1), 3ω=1ω (a2) +2ω. However, it implies there are four different emission directions, as shown with 3ω30, 3ω03, 3ω21, and 3ω12 in Figure 3, because of the different phase-matching relation. Harmonics 3ω30 or 3ω03, are undoubtedly emitted along the incident directions because only one linear momentum is related. However, for the other two ways, it is questionable that the photon with an energy of 2ω originates from 2ω20, 2ω02, or 2ω11. Taking 3ω21 as an example, each photon of 3ω21 may be transformed by one photon of a1 and one photon of 2ω11, or by one photon of a2 and one photon of 2ω02 (this selection rule is the same as that in non-collinear gas HHG). For the former, according to Equation (4), the coordinate of 3ω21 in the k-spectrum distribution should be (2.9, 0.76), and the emission angle (α) should be 0.25 rad. Conversely, for the latter, the coordinate of 3ω21 in the k-spectrum distribution should be (2.85, 0.95), and the emission angle should be 0.32 rad. The former selection rule is evidenced by the PIC simulations, as shown in Figure 3. In addition, according to our chain selection rule, each photon of 4ω31 should be transformed by one photon of a1 and one photon of 3ω21, and its coordinate in the k-spectrum distribution is expected to be (3.71, 1.5) and the emission angle 0.37 rad, instead of the (3.58, 1.79) coordinate and the 0.464 rad emission angle in the gas HHG way (one photon of a2 and one photon of 3ω30). This expectation is also confirmed by the simulation result in Figure 3.
![]()
Figure 3.The spectrum distribution of harmonics in
To further verify this conclusion, we show the second harmonic (2ω11), third harmonic (3ω21), and the fourth harmonic (4ω31) in Figure 4. Figures 4(d)–4(f) demonstrate the electric field distributions of the constant phase planes, where the emission angle is selected according to Equation (4). The distributions meet our expectations. We also note that the intensities of the relatively low-order harmonics are in the relativistic range in the present a0 = 3 case, with the normalized amplitude around 1, basically following the high energy conversion efficiency rule in plasma HHG. The emission angle is about two orders of magnitude higher than that (usually, in the milliradian level) in the non-collinear gas HHG.
![]()
Figure 4.Electric field (
4 Discussion
Here, two points are elucidated. According to the angular momentum conservation, the n = 2m order harmonics in the normal direction should be linearly polarized, because one photon of such harmonics stems from m photons of a1 and m photons of a2, and the total spin angular momentum is zero. The other harmonics are circularly (or elliptically) polarized, because one photo of such harmonics is transformed by one photon of its adjacent (n – 1)th-order harmonic and one photon of the input laser (CP laser). In fact, the PIC simulation result confirms this point; see the k-space spectrum distribution of Ey in the Supplementary Material where the even harmonics in the normal direction are missing. We also compared these results with those obtained in the cases of purely linearly polarized incident beams. In the case of p-polarized laser case, harmonics include both the odd and even orders in y component. In the case of s-polarized case, there are only odd order harmonics in z component and even order harmonics in y component. These results are in agreement with the conclusion in Ref. [10]. The emission angle for the same order harmonic is identical with that in the CP incident lasers case because it is determined by the same selection rule. Second, phase matching ensures that there is no wave vector mismatch between the emitted harmonics and the input beams which contributes to its emission, usually in the case of small enough crossing angle between the input beams, and these harmonics at different locations can hardly be distinguished spatially. However, in the present large crossing angle geometry, the projection of the input beam wave vectors along the harmonic emission direction should be considered, which results in a phase mismatch, expressed as
For the HHG from the laser–plasma interaction, one of the most significant findings is that the roll-off of the harmonic spectrum exhibits a power-law dependence of Iωn ~ ω-8/3, and the cutoff frequency increases with the laser intensity by ωcut-off ~ IL2.5[11,34]. Our results basically follow these findings for the same plasma HHG mechanism. Our selection rule is still valid for the different intensities and crossing angles, confirmed by additional simulations in the cases of a0 = 0.2, 0.5, 3, 10, 20, 50 when the half crossing angle is π/4 and a0 = 3 when the half crossing angle is π/8 and π/3. That is, for the same crossing angle, the intensity and cut-off frequency of the harmonics rise with the input laser intensity. On the other hand, for the same input lasers, the superposed electric field acting on electrons in the surface layer will be strengthened with the decrease of the crossing angle, which will also enhance the harmonics and extend the cut-off frequency. According to the simulation results, we found the conversion efficiency follows the power-law dependence of ~ω-4.1 as shown in Figure 5(a) for the harmonics in the reflected directions. For the same order harmonics emitted at different angles, the conversion efficiency (intensity) decreases with the emission angle, as shown in Figure 5(b).
![]()
Figure 5.(a) Energy conversion efficiency for the harmonics in the reflected directions. (b) Energy conversion efficiency for the harmonics of the same order emitted at different angles.
Although the emission angles of the harmonics obtained from the phase-matching equation agree well with the simulation results, we find a slight angle mismatch, as shown in Figures 3 and 4. The main reason is the deformation of the surface plane and Doppler effect of the reflected laser pulse. If the highly relativistic laser pulse is used, the radiation pressure dominates in the laser–plasma interaction, and there will be a curve for the surface electron layer, which may deflect the reflected pulses and impact the emission angle slightly. At the same time, red shift effect will occur for the lasers (harmonics) reflected from the election layer. We know that the motion velocity of the surface electron layer increases with the laser intensity and decreases with the target density, i.e.,
![]()
Figure 6.The spectrum distribution of harmonics in
Harmonics can also be modulated angularly directly from laser irradiated gratings, which has been demonstrated theoretically and experimentally. The approach using a single-beam scheme with grating targets results from the target (grating) modulation directly. In our approach, by overlapping two non-collinear lasers on the plasma target, the spatial structure of the driving field is imprinted on the electron dynamics and, hence, on the harmonic generation. The generated harmonics contain the information of the two incident laser pulses, and thus one can adjust the incident lasers for the different harmonic emission. Most importantly, we found the new phase-selection rule, which is the feature for the non-collinear plasma HHG mechanism, and the harmonic emission direction can be obtained. In addition, the non-collinear plasma HHG process is not limited to mixing two input beams of the same wavelength. When two-color input pulses are used, the selection rule is more complicated because there are additional electron oscillation frequencies except 1ω and 2ω which determines the HHG process. The selection rule of the phasing matching to generate harmonics is similar to what we obtained.
The computational precision in the PIC simulation may also affect the simulation results, particularly for those of order higher than the fourth. We check this by conducting another two-dimensional (2D) PIC simulation with 10,000×10,000 grids instead of 1000×1000 for the x×y window in the aforementioned 3D simulation. Apparently, there is nearly no difference between the harmonics in this case and those analyzed earlier (see the k-space spectrum distribution in the 2D case in the Supplementary Material).
5 Conclusion
In summary, we have proposed an approach, based on the non-collinear plasma HHG process, for generating angularly isolated harmonics at large emission angles. When two counter-rotation CP lasers hit a plasma target at the same side in V-shape, the harmonics carrying the information of the two input lasers are isolated. Using the momentum vector addition of photons, the propagating direction has been obtained. With the present scheme, the origin of these harmonics radiated in the relativistic laser and plasma interaction was elucidated for the first time. Both theoretical analysis and 3D PIC simulations confirmed the newly derived phase-matching selection rule for generating high harmonics. Thus, it is meaningful for practical applications and for understanding the plasma HHG process.
Multi-angle imaging is a potential application for these angularly isolated harmonics. Conventionally, to obtain more detailed imaging information, more than one laser pulses with different wavelengths are required to probe the sample simultaneously from different directions. The application of multiple pump lasers in an optical band will challenge the experimental layout and temporal synchronization. Therefore, angularly isolated multi-wavelength lasers generated simultaneously using the non-collinear HHG approach present significant application promise, particularly in biomedical imaging and material detection. In addition to such application as the gas harmonic source, one can extend its application in laser–plasma interaction, taking advantage of the high intensity of the plasma harmonic source. Although the plasma harmonic source has not efficiently been used so far owing to the strict requirement for the laser condition (intensity, contrast, etc.), there are some exclusive advantages for this harmonic source, such as high intensity/flux and large crossing angle, and this will certainly broaden the application field. Moreover, with the development of the laser technique and the experimental skill, the plasma harmonic source application is expected to flourish in the near future.
References
[1] M. C. Kohler, T. Pfeifer, K. Z. Hatsagortsyan, C. H. Keitel, P. Berman, E. Arimondo, C. LinAdvances in Atomic, Molecular, and Optical Physics, 159-208(2012).
[2] P. Jaeglé, J. A. R. Samson, D. L. EdererVacuum Ultraviolet Spectroscopy, 101-118(2000).
[3] C. Hernandez-Garcia, A. Picon, J. San Roman, L. Plaja. Phys. Rev. Lett., 111, 083602(2013).
[4] S. Patchkovskii, M. Spanner. Nat. Phys., 8, 707(2012).
[5] E. Goulielmakis, M. Schultze, M. Hofstetter, V. S. Yakovlev, J. Gagnon, M. Uiberacker, A. L. Aquila, E. M. Gullikson, D. T. Attwood, R. Kienberger, F. Krausz, U. Kleineberg. Science, 320, 1614(2008).
[6] X. M. Feng, S. Gilbertson, H. Mashiko, H. Wang, S. D. Khan, M. Chini, Y. Wu, K. Zhao, Z. H. Chang. Phys. Rev. Lett., 103, 183901(2009).
[7] C. Winterfeld, C. Spielmann, G. Gerber. Rev. Mod. Phys., 80, 117(2008).
[8] Y. Nomura, R. Horlein, P. Tzallas, B. Dromey, S. Rykovanov, Z. Major, J. Osterhoff, S. Karsch, L. Veisz, M. Zepf, D. Charalambidis, F. Krausz, G. D. Tsakiris. Nat. Phys., 5, 124(2009).
[9] S. V. Bulanov, N. M. Naumova, F. Pegoraro. Phys. Plasmas, 1, 745(1994).
[10] R. Lichters, J. Meyer-ter-Vehn, A. Pukhov. Phys. Plasmas, 3, 3425(1996).
[11] T. Baeva, S. Gordienko, A. Pukhov. Phys. Rev. E, 74, 046404(2006).
[12] B. Dromey, M. Zepf, A. Gopal, K. Lancaster, M. S. Wei, K. Krushelnick, M. Tatarakis, N. Vakakis, S. Moustaizis, R. Kodama, M. Tampo, C. Stoeckl, R. Clarke, H. Habara, D. Neely, S. Karsch, P. Norreys. Nat. Phys., 2, 456(2006).
[13] A. Pukhov. Nat. Phys., 2, 439(2006).
[14] B. Dromey, S. Kar, C. Bellei, D. C. Carroll, R. J. Clarke, J. S. Green, S. Kneip, K. Markey, S. R. Nagel, P. T. Simpson, L. Willingale, P. McKenna, D. Neely, Z. Najmudin, K. Krushelnick, P. A. Norreys, M. Zepf. Phys. Rev. Lett., 99, 085001(2007).
[15] K. Q. Pan, D. Yang, L. Guo, Z. C. Li, S. W. Li, C. Y. Zheng, S. E. Jiang, B. H. Zhang, X. T. He. High Power Laser Sci. Eng., 7(2019).
[16] B. F. Shen, J. Meyer-ter-Vehn. Phys. Plasmas, 8, 1003(2001).
[17] G. Stupakov. Phys. Rev. Lett., 102, 074801(2009).
[18] Y. Yu, B. Shen, L. Ji, X. Zhang, W. Wang, X. Zhao, X. Wang, L. Yi, Y. Shi, T. Xu. Phys. Plasmas, 20, 033109(2013).
[19] M. V. Frolov, N. L. Manakov, A. A. Minina, N. V. Vvedenskii, A. A. Silaev, M. Y. Ivanov, A. F. Starace. Phys. Rev. Lett., 120, 263203(2018).
[20] X. M. Zhang, B. F. Shen, Y. Shi, L. G. Zhang, L. L. Ji, X. F. Wang, Z. Z. Xu, T. Tajima. New J. Phys., 18, 083046(2016).
[21] T. Suzuki, T. F. Heinz. Opt. Lett., 14, 1201(1989).
[22] D. D. Hickstein, F. J. Dollar, P. Grychtol, J. L. Ellis, R. Knut, C. Hernandez-Garcia, D. Zusin, C. Gentry, J. M. Shaw, T. T. Fan, K. M. Dorney, A. Becker, A. Jaron-Becker, H. C. Kapteyn, M. M. Murnane, C. G. Durfee. Nat. Photonics, 9, 743(2015).
[23] J. B. Bertrand, H. J. Worner, H. C. Bandulet, E. Bisson, M. Spanner, J. C. Kieffer, D. M. Villeneuve, P. B. Corkum. Phys. Rev. Lett., 106, 023001(2011).
[24] M. Cerchez, A. L. Giesecke, C. Peth, M. Toncian, B. Albertazzi, J. Fuchs, O. Willi, T. Toncian. Phys. Rev. Lett., 110, 065003(2013).
[25] G. Cantono, L. Fedeli, A. Sgattoni, A. Denoeud, L. Chopineau, F Reau, T. Ceccotti, A. Macchi. Phys. Rev. Lett., 120, 264803(2018).
[26] K. T. Kim, C. M. Zhang, A. D. Shiner, S. E. Kirkwood, E. Frumker, G. Gariepy, A. Naumov, D. M. Villeneuve, P. B. Corkum. Nat. Phys., 9, 159(2013).
[27] C. M. Heyl, S. N. Bengtsson, S. Carlstrom, J. Mauritsson, C. L. Arnold, A. L'Huillier. New J. Phys., 16, 052001(2014).
[28] M. Negro, M. Devetta, D. Facciala, A. G. Ciriolo, F. Calegari, F. Frassetto, L. Poletto, V. Tosa, C. Vozzi, S. Stagira. Opt. Express, 22, 29778(2014).
[29] F. Q. Kong, C. M. Zhang, F. Bouchard, Z. Y. Li, G. G. Brown, D. H. Ko, T. J. Hammond, L. Arissian, R. W. Boyd, E. Karimi, P. B. Corkum. Nat. Commun., 8, 14970(2017).
[30] J. L. Ellis, K. M. Dorney, C. G. Durfee, C. Hernandez-Garcia, F. Dollar, C. A. Mancuso, T. T. Fan, D. Zusin, C. Gentry, P. Grychtol, H. C. Kapteyn, M. M. Murnane, D. D. Hickstein. Opt. Express, 25, 10126(2017).
[31] U. Teubner, P. Gibbon. Rev. Mod. Phys., 81, 445(2009).
[32] J. Gao, B. Li, F. Liu, Z.-Y. Chen, M. Chen, X. Ge, X. Yuan, L. Chen, Z. Sheng, J. Zhang. Phys. Rev. E, 101, 033202(2020).
[33] Z. Y. Chen, A. Pukhov. Nat. Commun., 7, 12515(2016).
[34] U. Teubner, G. Pretzler, T. Schlegel, K. Eidmann, E. Forster, K. Witte. Phys. Rev. A, 67, 013816(2003).
[35] T. D. Arber, K. Bennett, C. S. Brady, A. Lawrence-Douglas, M. G. Ramsay, N. J. Sircombe, P. Gillies, R. G. Evans, H. Schmitz, A. R. Bell, C. P. Ridgers. Plasma Phys. Control. Fusion, 57, 113001(2015).
[36] L. L. Ji, B. F. Shen, D. X. Li, D. Wang, Y. X. Leng, X. M. Zhang, M. Wen, W. P. Wang, J. C. Xu, Y. H. Yu. Phys. Rev. Lett., 105, 025001(2010).
[37] X. M. Zhang, B. F. Shen, X. M. Li, Z. Y. Jin, F. C. Wang. Phys. Plasmas, 14, 073101(2007).
[38] X. M. Zhang, B. F. Shen, X. M. Li, Z. Y. Jin, F. C. Wang, M. Wen. Phys. Plasmas, 14, 123108(2007).
[39] A. Macchi, F. Cattani, T. V. Liseykina, F. Cornolti. Phys. Rev. Lett., 94, 165003(2005).

Set citation alerts for the article
Please enter your email address



