Snapshot spectral compressive imaging reconstruction using convolution and contextual Transformer

Lishun Wang; Zongliang Wu; Yong Zhong; Xin Yuan

doi:10.1364/PRJ.458231

Abstract

Spectral compressive imaging (SCI) is able to encode a high-dimensional hyperspectral image into a two-dimensional snapshot measurement, and then use algorithms to reconstruct the spatio-spectral data-cube. At present, the main bottleneck of SCI is the reconstruction algorithm, and state-of-the-art (SOTA) reconstruction methods generally face problems of long reconstruction times and/or poor detail recovery. In this paper, we propose a hybrid network module, namely, a convolution and contextual Transformer (CCoT) block, that can simultaneously acquire the inductive bias ability of convolution and the powerful modeling ability of Transformer, which is conducive to improving the quality of reconstruction to restore fine details. We integrate the proposed CCoT block into a physics-driven deep unfolding framework based on the generalized alternating projection (GAP) algorithm, and further propose the GAP-CCoT network. Finally, we apply the GAP-CCoT algorithm to SCI reconstruction. Through experiments on a large amount of synthetic data and real data, our proposed model achieves higher reconstruction quality (

> 2 dB

in peak signal-to-noise ratio on simulated benchmark datasets) and a shorter running time than existing SOTA algorithms by a large margin. The code and models are publicly available at https://github.com/ucaswangls/GAP-CCoT.

1. INTRODUCTION

A hyperspectral image is a spatio-spectral data-cube consisting of many narrow spectral bands, each spectral band corresponding to a wavelength. Compared with RGB images, hyperspectral images have rich spectral information and can be widely used in medical diagnosis [1], food safety [2], remote sensing [3], and other fields. However, the long imaging time and high hardware cost of existing hyperspectral cameras greatly limit the application of these devices. To address the above problems, spectral compressive imaging (SCI), especially the coded aperture snapshot spectral imaging (CASSI) system [1,4,5], provides an elegant solution, which can capture information from multiple spectral bands at the same time with only one two-dimensional (2D) sensor. CASSI uses a physical mask and a prism to modulate the spectral data-cube, and captures the modulated and compressed measurement on a 2D plane sensor. Then reconstruction algorithms are employed to recover the hyperspectral data-cube from the measurement along with the mask. This paper focuses on the reconstruction algorithm.

At present, SCI reconstruction algorithms mainly include model-based methods and learning-based methods. Traditional model-based methods have relevant theoretical proofs and can be well explained. The representative algorithms are mainly TWo-step Iterative Shrinkage/Thresholding algorithm (TwIST) [6], generalized alternating projection total variation (GAP-TV) [7], and DEcompress SCI (DeSCI) [8]. However, model-based methods require prior knowledge and long reconstruction times and usually provide only poor reconstruction quality. With its strong fitting ability, a deep learning model can directly learn the relevant knowledge from data and provide excellent reconstruction results [9 –13]. However, compared to model-based methods, learning-based methods lack interpretability [14].

The deep unfolding network driven by physics combines the advantages of model-based and learning-based methods, so it is powerful with clear interpretability [15 –18]. At present, most advanced reconstruction algorithms [19,20] are based on the idea of deep unfolding. Many models combine U-net [21] with the deep unfolding idea for image reconstruction and achieve good reconstruction results. However, the U-net model is too simple to fully capture the effective information of the image. Therefore, we use the inductive bias ability of convolution and the powerful modeling ability of Transformer [22] to design a parallel module to solve the problem of SCI reconstruction. As shown in Fig. 1, the integration of our proposed method and deep unfolding idea can recover more details with fewer artifacts.

Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you！Sign up now

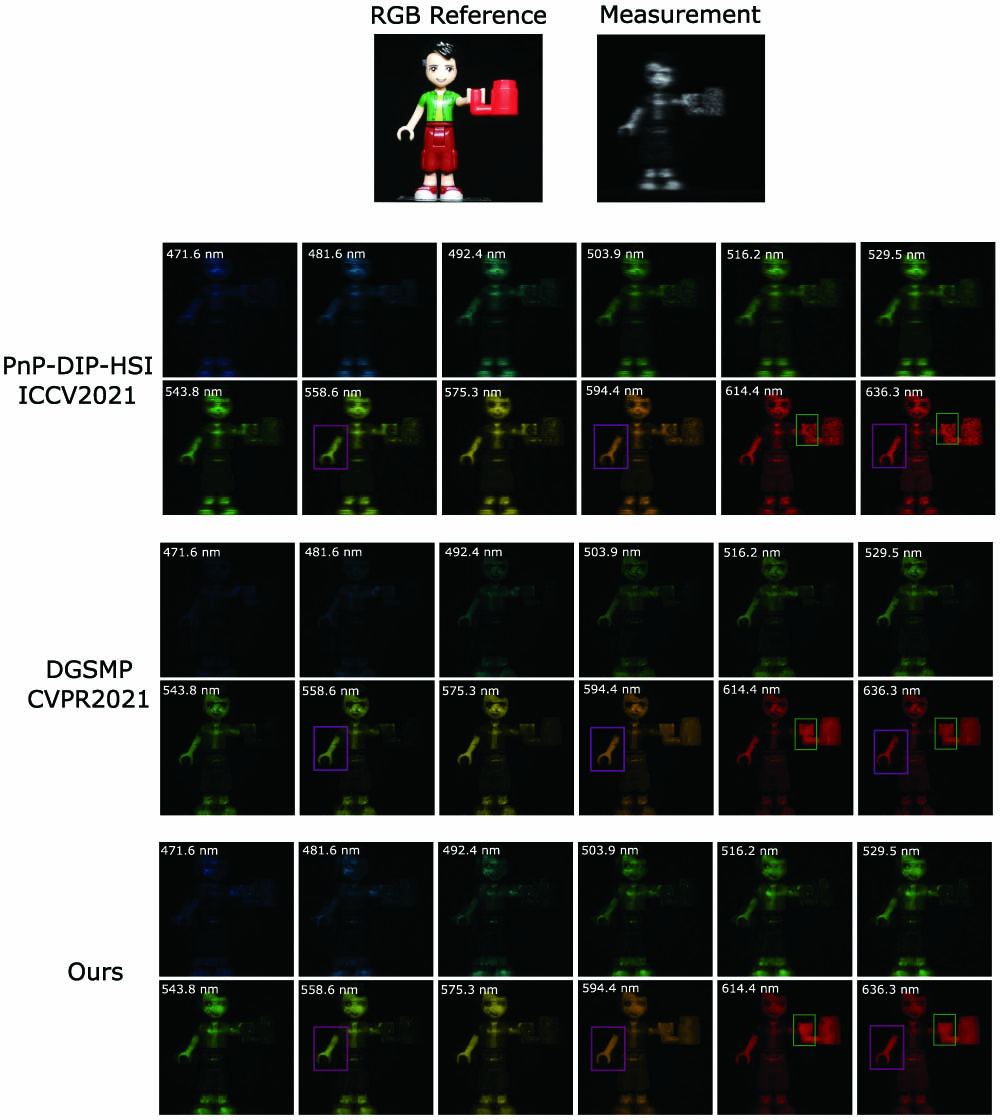
Figure 1.Reconstructed real data of Legoman, captured by snapshot SCI systems in Ref. [20]. We show reconstruction results of 12 spectral channels, and compare our proposed method with the latest self-supervised method (PnP-DIP-HSI [23]) and the method based on maximum a posteriori (MAP) estimation (DGSMP algorithm [24]). As can be seen from the purple and green areas in the plot, our method reconstructs a clearer image, the PnP-DIP-HSI method produces some artifacts, and the DGSMP method loses some details.

Our main contributions in this paper are summarized as follows: •we first apply Transformer to deep unfolding for SCI reconstruction;•we propose an effective parallel network structure composed of convolution and contextual Transformer (CCoT), which can obtain more spectral features;•experimental results on a large amount of synthetic and real data show that our proposed method achieves state-of-the-art (SOTA) results in SCI reconstruction;•the proposed method can also be used in other compressive sensing (CS) systems [25,26], such as video CS [27–29], and yields excellent results.

2. RELATED WORK

In this section, we first review the forward model of CASSI, and then briefly introduce existing reconstruction methods. Focusing on deep-learning-based models, we describe the pros and cons of convolutional neural networks (CNNs) and introduce the vision Transformer (ViT) for other tasks.

A. Mathematical Model of SCI System

The SCI system encodes a high-dimensional spectral data-cube into 2D measurement, and CASSI [4] is one of the earliest SCI systems. As shown in Fig. 2, the three-dimensional (3D) spatio-spectral data-cube is first modulated by a coded aperture (a.k.a., mask). Then, the encoded 3D spectral data-cube is dispersed by the prism. Finally, the entire (modulated) spectral data-cube is captured by a 2D camera sensor by integrating across the spectral dimension.

Figure 2.Schematic diagrams of CASSI system.

Let $F \in R^{n_{x} \times n_{y} \times n_{λ}}$ denote the captured 3D spectral data-cube, and $M \in R^{n_{x} \times n_{y}}$ denote a pre-defined mask, where $n_{x}$ , $n_{y}$ , and $n_{λ}$ represent the height, width, and channel number of the spectral image, respectively. For each spectral channel $ℓ = 1, \dots, n_{λ}$ , the spectral image is modulated to $F_{ℓ}^{'} = F_{ℓ} ⊙ M$ , where $F_{ℓ}$ and $F_{ℓ}^{'}$ represent the original and modulated spectral images at the $ℓ$ th spectral channel, respectively, and $⊙$ denotes element-wise multiplication. Then after passing through the dispersive prism, the modulated spectral data-cube is tilted. Finally, by compressing across the spectral domain, the camera sensor captures a 2D compressed measurement $G \in R^{n_{x} \times (n_{y} + n_{λ} - 1)}$ , which can be expressed as $G_{u, v} = \sum_{ℓ = 1}^{n_{λ}} F_{u, v, l}^{''} + Z_{u, v},$ (1)where $(u, v)$ represents the coordinate system of the camera detector plane, $F_{u, v, l}^{''} = F_{x, y + d (λ_{ℓ} - λ_{c}), ℓ}^{'}$ denotes the tilted spectral data-cube after passing through the dispersive prism of the $ℓ$ th spectral channel, $(x, y)$ represents the coordinate system of each modulated spectral image, $d (λ_{ℓ} - λ_{c})$ represents the spatial shifting of the $ℓ$ th spectral channel where $d$ is a scalar, $λ_{ℓ}$ is the wavelength at the $ℓ$ th channel, $λ_{c}$ denotes the reference wavelength that does not shift after passing through the disperser, and $Z \in R^{n_{x} \times (n_{y} + n_{λ} - 1)}$ denotes the measurement noise.

For the sake of simple notations, as derived in Ref. [23], we further give the vectorized formulation expression of Eq. (1). First, we define $vec (\cdot)$ as a vectorization operation of a matrix. Then we vectorize $g = vec (G) \in R^{n_{x} (n_{y} + n_{λ} - 1)}$ , $z = vec (Z) \in R^{n_{x} (n_{y} + n_{λ} - 1)}$ , and $f = {[f_{1}^{T}, \dots, f_{n_{λ}}^{T}]}^{T} \in R^{n_{x} n_{y} n_{λ}}$ , where $f_{ℓ} = vec (F_{ℓ})$ . In addition, we define the sensing matrix generated by a coded aperture and disperser in the CASSI system as $H = [D_{1}, \dots, D_{n_{λ}}] \in R^{n_{x} (n_{y} + n_{λ} - 1) \times n_{x} n_{y} n_{λ}},$ (2)where $D_{ℓ} = [\begin{matrix} 0^{(1)} \\ A_{ℓ} \\ 0^{(2)} \end{matrix}] \in R^{n_{x} (n_{y} + n_{λ} - 1) \times n_{x} n_{y}}$ , where $A_{ℓ} = Diag (vec (M)) \in R^{n_{x} n_{y} \times n_{x} n_{y}}$ is a diagonal matrix and its diagonal element is $vec (M)$ , and $0^{(1)} \in R^{(ℓ - 1) \times n_{x} n_{y}}$ and $0^{(2)} \in R^{(n_{λ} - ℓ) \times n_{x} n_{y}}$ represent the zero matrix. Finally, the vectorization expression of Eq. (1) is $g = H f + z .$ (3)

After obtaining the measurement $g$ , the next task is to develop a decoding algorithm. Given $g$ and $H$ , solve $f$ .

B. Reconstruction Algorithms for SCI

SCI reconstruction algorithms mainly focus on how to solve the ill-posed inverse problem in Eq. (3), a.k.a., the reconstruction of SCI. Traditional methods are generally based on prior knowledge as a regularization condition to solve the problem, such as using TV [6], sparsity [30], dictionary learning [31,32], non-local low rank [8,33], and Gaussian mixture modes [34]. The main problem of these algorithms is that they need to manually set prior knowledge and iteratively solve the problem. Therefore, the reconstruction time is long, and the quality is usually not good.

With its powerful learning capability, the neural network can directly learn a mapping relationship from the measurement to the original hyperspectral image, and the reconstruction speed can reach the millisecond level. End-to-end (E2E) deep learning methods (Spatial-Spectral Self-Attention network (TSA-net) [35], $λ$ -net [9], Spatial/Spectral Invariant Residual U-Net (SSI-ResU-Net) [10]) take the measurement and masks as inputs, and use only one single network to reconstruct the desired signal directly. Plug-and-play (PnP) methods [36,37] use a pre-trained network as a denoiser plugged into iterative optimization [7,38]. Different from PnP methods, the denoising networks at each stage of deep unfolding methods [19,20] are independent of each other, and the parameters are not shared, and thus can be trained E2E.

Deep unfolding is driven by physics and offers the advantages of high-speed, high-quality reconstruction while enjoying the benefits of physics-driven interpretability. Therefore, in this paper, we follow the deep unfolding framework [20] and propose a new deep denoiser block based on CCoT. The proposed module along with deep unfolding leads to SOTA results for SCI reconstruction.

C. Limitations of CNNs for Reconstruction

Due to local connection and shift-invariance, the convolutional network [39] can well extract local features of images, and is widely used in image recognition [40 –42], object detection [43], semantic segmentation [44], image denoising [45], and other tasks [46,47]. However, its local connection property also makes it lack the ability of global perception. To improve the receptive field of convolution, deeper network architecture [41] or various pooling operations [48] are often used. The squeeze-and-excitation network (SENet) [48] uses the channel attention (CA) mechanism [49] to aggregate the global context and redistributes the weight to each channel. However, these methods usually lose a significant amount of detail information and are not friendly to image reconstruction and other tasks that need to recover local details.

Bearing the above concerns and considering the running time, we do not use very deep network structure in our work for SCI reconstruction. Instead, we use a convolution with a sliding step of two instead of the traditional max pooling operation, aiming to capture the local details of the desired spatio-spectral data-cube.

D. Vision Transformers

ViT [50] and its variants [51 –54] have verified the effectiveness of Transformer architecture in computer vision tasks. However, training a good ViT model requires a large number of training datasets (i.e., JFT-300M [55]), and its computational complexity increases quadratically with image size. To better apply Transformer to computer vision related tasks, the latest Swin Transformer [56] proposes a local window self-attention mechanism and a shifting window method, which greatly reduces computational complexity. The Transformer network based on Swin has achieved amazing results in computer vision tasks such as image recognition [57], object detection [58], semantic segmentation [59,60], and image restoration [61], which further verifies the feasibility of Transformer in computer vision. In addition, when computing self-attention, most Transformers including Swin Transformer are independently learned for all pairwise query-keys, without using the rich contextual relations between them. Moreover, the self-attention mechanism in ViTs often ignores local feature details, which is not conducive to low-level image tasks such as image reconstruction.

Inspired by contextual Transformer (CoT) [62] and conformer networks [63], in this paper, we propose a network structure named CCoT, which can take advantage of convolution and Transformer to extract more effective spectral features, and can be well applied to image reconstruction tasks such as SCI.

3. PROPOSED NETWORK

In this section, we first briefly review the GAP-net [20] algorithm, which uses deep unfolding ideas [64] and the GAP algorithm [65] for SCI reconstruction. We select GAP-net because of its high performance, robustness, and flexibility for different SCI systems reported in Ref. [20]. Following this, we combine the advantages of convolution and Transformer and then propose a module named CCoT. We integrate this module into GAP-net to reconstruct hyperspectral images from the compressed measurements and masks.

A. Review of GAP-net for SCI Reconstruction

The SCI reconstruction algorithm is used to solve the following optimization problem: $\hat{f} = \underset{f}{\arg \min} \frac{1}{2} ∥ g - H f ∥^{2} + λ Ω (f),$ (4)where the first term is the fidelity term, and the second term, $Ω (f)$ , is the prior or regularization to confine the solutions. In GAP-net and other deep unfolding algorithms, implicit priors (represented by deep neural networks) have been used to improve the performance.

Following the framework of GAP, Eq. (4) can be rewritten as a constrained optimization problem by introducing an auxiliary parameter $v$ : $(\hat{f}, \hat{v}) = \underset{f, v}{\arg \min} \frac{1}{2} ∥ f - v ∥_{2}^{2} + λ Ω (v), s . t . g = H f .$ (5)

To solve Eq. (5), GAP decomposes it into the following subproblems for iterative solutions, with $η$ denoting the iteration number. •Solving $f$ : $f^{(η + 1)}$ is updated via an Euclidean projection of $v^{(η)}$ on the linear manifold $M : g = H f$ : $f^{(η + 1)} = v^{(η)} + H^{T} {(H H^{T})}^{- 1} (g - H v^{(η)}) .$ (6)•Solving $v$ : we can apply a trained denoiser to map $f$ closer to the desired signal space: $v^{(η + 1)} = D_{η + 1} (f^{(η + 1)}),$ (7)where $D_{η + 1}$ denotes the denoising operation.

It has been derived in the literature [7] that Eq. (6) has a closed-form solution due to the special structure of $H$ in Eq. (2). Therefore, the only difference (and novelty) is the denoising step in Eq. (7). In the following, we describe the novel CCoT block proposed in this work for efficient and effective SCI reconstruction. The general reconstruction framework is illustrated in Fig. 3(a), and the detailed CCoT block is depicted in Figs. 3(b)–3(f).

Figure 3.Architecture of the proposed GAP-CCoT. (a) GAP-net with $N$ stages; $G (\cdot)$ represents the operation of Eq. (6), $D (\cdot)$ represents a denoiser, and $v^{(0)} = H^{T} g$ . (b) CCoT-net, the proposed denoising network plugged into GAP algorithm. (c) Convolution branch and Transformer branch; the output is connected with concatenation. (d) Convolution block with channel attention; $c$ represents the output number of convolution channels. (e) Contextual Transformer block. (f) Pixelshuffle algorithm for fast upsampling.

B. Proposed CCoT Block for Deep Denoising

As mentioned in Section 2.D, to address the challenge of SCI reconstruction, we develop the CCoT block, in which convolution and Transformer are used in parallel, which can be well applied to image reconstruction tasks such as SCI.

1. Convolution Branch

As shown in Figs. 3(c) and 3(d), the convolution branch consists of a down-sampling layer and a CA block. In this paper, we use convolution layer for down-sampling with sliding step $s$ instead of direct max pooling to capture fine details, and $s = 2$ is used in the experiments. The CA block draws lessons from the idea of SENet [48], automatically obtains the importance of each feature channel by learning, then improves useful features according to this importance and suppresses features that are not significant for the current task. The first convolution layer and CA module are followed by a LeakyReLU activation function [66]. The proposed convolution branch can extract local features of images well.

2. Contextual Transformer Branch

By calculating the similarity between pixels, the traditional Transformer makes the model focus on different regions and extract more effective features. However, when calculating paired query-keys, they are relatively independent. A single spectral image itself contains rich contextual information, and there is also a significant amount of correlations between adjacent spectra. Therefore, we designed a CoT branch to better obtain features of hyperspectral images.

As shown in Fig. 3(c), the CoT branch consists of a down-sampling layer and a CoT block. The structure of the down-sampling layer is the same as the convolution branch. As shown in Fig. 3(e), we first recall that the input of the hyperspectral image is of $F \in R^{n_{x} \times n_{y} \times n_{λ}}$ . Then we define queries, keys, and values as $K_{1} \in R^{n_{x} \times n_{y} \times n_{λ}}$ , $Q \in R^{n_{x} \times n_{y} \times n_{λ}}$ , $V \in R^{n_{x} \times n_{y} \times n_{λ}}$ , respectively. Different from the traditional self-attention that uses $1 \times 1$ convolutions to generate mutually independent paired query-keys, the CoT block first applies the group convolution of size $m \times m$ to generate a static key $K_{1} \in R^{n_{x} \times n_{y} \times n_{λ}}$ containing the context, and $K_{1}$ can be used as a static context representation of input $F$ . $Q$ and $V$ can be generated by the traditional self-attention mechanism. Then, we concatenate $K_{1}$ and $Q$ by the third dimension (spectral channels), followed by two $1 \times 1$ convolutions to generate an attention matrix: $A = {Conv}_{1} ({Conv}_{2} ({[K_{1}, Q]}_{3})),$ (8)where ${[]}_{3}$ denotes the concatenation along the third dimension, ${Conv}_{1}, {Conv}_{2}$ represent two $1 \times 1$ convolutions, $A \in R^{n_{x} \times n_{y} \times (m^{2} \times C_{h})}$ represents the attention matrix containing context, and $C_{h}$ denotes the number of attention heads. We use the traditional self-attention mechanism to perform a weighted summation of $V$ through $A$ to obtain the dynamic context $K_{2} \in R^{n_{x} \times n_{y} \times n_{λ}}$ , and then fuse dynamic context $K_{2}$ and static context $K_{1}$ as the output of the CoT block through the attention mechanism [48].

Finally, we concatenate the output of the convolution branch and CoT branch as the final output of the CCoT block.

C. GAP-CCoT Network

As shown in Fig. 3(b), we use the CCoT module and pixelshuffle algorithm to construct a U-net [21] like network as the denoiser in GAP-net. The network consists of a contracting path and an expansive path. The contracting path contains three CCoT modules, and the expansive path contains three up-sampling modules. Each module of the expansive path is first quickly up-sampled by the pixelshuffle algorithm [67], followed by a $3 \times 3$ convolution, and finally concatenates the output from the corresponding stage of the contracting path (after a $1 \times 1$ convolution) as the input of the next module. Eventually, CCoT, GAP, and deep unfolding form the reconstruction network (GAP-CCoT) of SCI.

Last, following GAP-net [20] and hyperspectral image reconstruction using a deep Spatial-Spectral Prior (HSSP) [19] network, the loss function of the proposed model is $L_{MSE} (Θ) = \frac{1}{n_{λ}} \sum_{ℓ = 1}^{n_{λ}} {∥ {\hat{F}}_{ℓ} - F_{ℓ} ∥}_{2}^{2},$ (9)where $L_{MSE} (Θ)$ represents the mean square error (MSE) loss, $n_{λ}$ again represents the spectral channel to be reconstructed, and ${\hat{F}}_{ℓ} \in R^{n_{x} \times n_{y}}$ is the reconstructed hyperspectral image at the $ℓ$ th spectral channel.

4. EXPERIMENTAL RESULTS

In this section, we compare the performance of the proposed GAP-CCoT network with several SOTA methods on both simulation and real datasets. The peak-signal-to-noise-ratio (PSNR) and structured similarity index metrics (SSIM) [68] are used to evaluate the performance of different hyperspectral image reconstruction methods.

A. Datasets

We use the hyperspectral dataset CAVE [69] for model training and KAIST [70] for model simulation testing. The CAVE dataset consists of 32 scenes, including full spectral resolution reflectance data from 400 nm to 700 nm with a 10 nm step, and a spatial resolution of $512 \times 512$ . The KAIST dataset consists of 30 scenes with a spatial resolution of $2704 \times 3376$ . To match the wavelength of the real CASSI system, we follow the method proposed by TSA-net [71] and employ the spectral interpolation method to modify the training set and test data wavelength. The final wavelength was fitted to 28 spectral bands ranging from 450 nm to 650 nm.

B. Implementation Details

During training, we use random cropping, rotation, and flipping for CAVE dataset augmentation. By simulating the imaging process of CASSI, we can obtain the corresponding measurement. We use measurement and masks as inputs to train GAP-CCoT and use the Adam optimizer [72] to optimize the model. The learning rate is set to 0.001 initially and reduces by 10% every 10 epochs. Our model is trained for 200 epochs in total. All experiments are run on the NVIDIA RTX 8000 GPU using PyTorch.

Finally, we use a GAP-CCoT network with nine stages as the reconstruction network, and no noise is added to the measurement during training on simulation data. We added shot noise to the measurements for model training on real data following the procedure in Ref. [20].

C. Simulation Results

We compare the method proposed in this paper with several SOTA methods (TwIST [6], GAP-TV [7], DeSCI [8], HSSP [19], $λ$ -net [9], TSA-net [71], GAP-net [20], Plug-and-Play Deep Image Priors Hyperspectral Images (PnP-DIP-HSI) [23], Deep Gaussian Scale Mixture Prior (DGSMP) [24] and SSI-ResU-Net (v1) [10]) on synthetic datasets. Table 1 presents the average PSNR and SSIM results of different spectral reconstruction algorithms. We can see that the average PSNR value of our proposed algorithm is 35.26 dB and average SSIM value is 0.950. The average PSNR value is 2.09 dB higher than that of the current best algorithm SSI-ResU-Net (v1, pre-printed, not published), and the SSIM value is 0.021 higher. In addition, compared with the self-supervised learning method PnP-DIP-HSI and DGSMP method (best published results) based on the maximum a posteriori (MAP) estimation, the average PSNR of our proposed method is 3.96 dB and 2.63 dB higher, respectively. Based on these significant improvements, we can conclude the powerful learning capability of Transformer and the proposed CCoT block.Table 1.

Average PSNR in dB (upper entry in each cell) and SSIM (lower entry in each cell) of Different Algorithms on 10 Synthetic Datasets^a

Algorithms	Scene 1	Scene 2	Scene 3	Scene 4	Scene 5	Scene 6	Scene 7	Scene 8	Scene 9	Scene 10	Average
TwIST [6]	24.81	19.99	21.14	30.30	21.68	22.16	17.71	22.39	21.43	22.87	$22.44 \pm 3.32$
TwIST [6]	0.730	0.632	0.764	0.874	0.688	0.660	0.694	0.682	0.729	0.595	$0.704 \pm 0.077$
GAP-TV [7]	25.13	20.67	23.19	35.13	22.31	22.90	17.98	23.00	23.36	23.70	$23.73 \pm 4.45$
GAP-TV [7]	0.724	0.630	0.757	0.870	0.674	0.635	0.670	0.624	0.717	0.551	$0.685 \pm 0.088$
DeSCI [8]	27.15	22.26	26.56	39.00	24.80	23.55	20.03	20.29	23.98	25.94	$25.35 \pm 5.38$
DeSCI [8]	0.794	0.694	0.877	0.965	0.778	0.753	0.772	0.740	0.818	0.666	$0.785 \pm 0.087$
HSSP [19]	31.48	31.09	28.96	34.56	28.53	30.83	28.71	30.09	30.43	28.78	$30.35 \pm 3.79$
HSSP [19]	0.858	0.842	0.832	0.902	0.808	0.877	0.824	0.881	0.868	0.842	$0.852 \pm 0.049$
$λ$ -net [9]	30.82	26.30	29.42	36.27	27.84	30.69	24.20	28.86	29.32	27.66	$29.14 \pm 3.20$
$λ$ -net [9]	0.880	0.846	0.916	0.962	0.866	0.886	0.875	0.880	0.902	0.843	$0.886 \pm 0.035$
TSA-net [71]	31.26	26.88	30.03	39.90	28.89	31.30	25.16	29.69	30.03	28.32	$30.15 \pm 3.92$
TSA-net [71]	0.887	0.855	0.921	0.964	0.878	0.895	0.887	0.887	0.903	0.848	$0.893 \pm 0.033$
PnP-DIP-HSI [23]	32.70	27.27	31.32	40.79	29.81	30.41	28.18	29.45	34.55	28.52	$31.30 \pm 3.98$
PnP-DIP-HSI [23]	0.898	0.832	0.920	0.970	0.903	0.890	0.913	0.885	0.932	0.863	$0.901 \pm 0.038$
GAP-net [20]	33.03	29.52	33.04	41.59	30.95	32.88	27.60	30.17	32.74	29.73	$32.13 \pm 3.81$
GAP-net [20]	0.921	0.903	0.940	0.972	0.924	0.927	0.921	0.904	0.927	0.901	$0.924 \pm 0.021$
DGSMP [24]	33.26	32.09	33.06	40.54	28.86	33.08	30.74	31.55	31.66	31.44	$32.63 \pm 3.07$
DGSMP [24]	0.915	0.898	0.925	0.964	0.882	0.937	0.886	0.923	0.911	0.925	$0.917 \pm 0.024$
SSI-ResU-Net (v1) [10]	34.06	30.85	33.14	40.79	31.57	34.99	27.93	33.24	33.58	31.55	$33.17 \pm 3.34$
SSI-ResU-Net (v1) [10]	0.926	0.902	0.924	0.970	0.939	0.955	0.861	0.949	0.931	0.934	$0.929 \pm 0.030$
Ours	35.17	35.90	36.91	42.25	32.61	34.95	33.46	33.13	35.75	32.43	$35.26 \pm 2.89$
Ours	0.938	0.948	0.958	0.977	0.948	0.957	0.923	0.952	0.954	0.941	$0.950 \pm 0.014$

Best results are in bold.

Figure 4 shows part of the visualization results and spectral curves of two scenes using several SOTA spectral SCI reconstruction algorithms. Enlarging the local area, we can see that our proposed method can recover more edge details and better spectral correlation than other algorithms.

Figure 4.Reconstruction results of GAP-CCoT and other spectral reconstruction algorithms ( $λ$ -net, HSSP, TSA-net, GAP-net, DGSMP, PnP-DIP-HSI) in scene 3 and scene 9. Zoom in for better view.

In addition, we also analyze the computational complexity of our method and compare it with several previous deep-learning-based SOTA spectral reconstruction algorithms. As shown in Table 2, our proposed GAP-CCoT-S3 (with three stages) achieves higher reconstruction quality than previous SOTA algorithms with lower computational cost.Table 2.

Computational Complexity and Average Reconstruction Quality of Several SOTA Algorithms on 10 Synthetic Datasets

Algorithm	Params ( $10^{6}$ )	FLOPs ( $10^{9}$ )	PSNR (dB)	SSIM
$λ$ -net [9]	66.16	514.33	29.25	0.886
TSA-net [71]	44.25	135.03	30.15	0.893
GAP-net [20]	2.89	54.16	32.13	0.924
DGSMP [24]	3.76	647.28	32.63	0.917
SSI-ResU-Net (v1) [10]	1.25	81.98	33.17	0.929
GAP-CCoT-S3	2.68	31.84	33.89	0.934
GAP-CCoT-S9	8.04	95.52	35.26	0.950

D. Flexibility of GAP-CCoT to Mask Modulation

CCoT-net serves only as a denoiser for the GAP algorithm, so the GAP-CCoT network proposed in this paper has flexibility for different signal modulations. To verify this, we train the GAP-CCoT network on one mask and test it on five other untrained masks. Table 3 shows the test results of the average PSNR value and SSIM value on 10 simulation data using different masks (five new masks of size $256 \times 256$ randomly cropped from the real mask of size $660 \times 660$ ). We can observe that for a new mask that does not appear in training, the average PSNR decrease remains within 0.27 dB, which is still better than other algorithms. Therefore, we can conclude that the GAP-CCoT network proposed in this paper is flexible for large-scale SCI reconstruction.Table 3.

Average PSNR and SSIM Results on 10 Synthetic Data with Different Masks

Mask	PSNR (dB)	SSIM
Mask used in training	$35.26 \pm 2.89$	$0.950 \pm 0.014$
New mask 1	$35.10 \pm 2.92$	$0.949 \pm 0.015$
New mask 2	$35.06 \pm 2.91$	$0.948 \pm 0.015$
New mask 3	$35.06 \pm 2.91$	$0.949 \pm 0.015$
New mask 4	$35.02 \pm 2.92$	$0.948 \pm 0.014$
New mask 5	$34.99 \pm 2.90$	$0.948 \pm 0.014$

Table 4.

Ablation Study: Average PSNR and SSIM Values of Different Algorithms on 10 Synthetic Data

Algorithms	PSNR (dB)	SSIM
Stacked CCoT w/o CoT	$32.86 \pm 3.01$	$0.924 \pm 0.021$
GAP-CCoT w/o CoT	$34.13 \pm 2.95$	$0.933 \pm 0.019$
Stacked CCoT	$34.27 \pm 2.94$	$0.936 \pm 0.018$
GAP-CCoT	$35.26 \pm 2.89$	$0.950 \pm 0.014$

E. Ablation Study

To verify the effectiveness of CoT and GAP algorithms, we trained two different GAP-CCoT networks and two different Stacked CCoT networks (shown in Fig. 5) for spectral SCI reconstruction, respectively. Table 4 shows the reconstruction results of the proposed two networks, where “w/o” CoT means removing the CoT branch at each stage of coding. We can clearly observe that the GAP-CCoT network is 0.99 dB higher in PSNR than the Stacked CCoT network. The PSNR value of the CoT module is improved by 1.13 dB and 1.41 dB on the GAP-CCoT network and Stacked CCoT network, respectively.

Figure 5.Architecture of the proposed Stacked CCoT. The input of the network is $H^{T} g$ , and CCoT-net is the same as in Fig. 3(b).

Figure 6.Effect of stage number on SCI reconstruction quality.

To verify the effect of the loss function on reconstruction quality, we use the least absolute deviation (LAD) loss function to retrain our proposed model. As shown in Table 6, our method can further improve the reconstruction quality by using the LAD loss function.Table 6.

Average PSNR and SSIM Results on 10 Synthetic Data with Different Loss Functions

Loss Function	PSNR (dB)	SSIM
LAD	35.48	0.952
MSE	35.26	0.950

F. Real Data Results

We test the proposed method on several real data captured by the CASSI system [4,71]. The system captures 28 spectral bands with wavelengths ranging from 450 nm to 650 nm. The spatial resolution of the object is $550 \times 550$ , and the spatial resolution of the measurements captured by the plane sensor is $550 \times 604$ . Due to the flexibility of our proposed method for different masks, we trained GAP-CCoT with a mask of spatial size $256 \times 256$ and directly applied it to real measurements with a spatial size of $550 \times 640$ . We compared our method with several SOTA methods ( $λ$ -net [9], TSA-net [71], GAP-net [20], PnP-DIP-HSI [23], DGSMP [24]) on real data. In addition to the results shown in Fig. 1, Fig. 7 shows partial visualization reconstructed results and spectral curves of real data from another scene. By zooming in on a local area, we can see that our proposed method can recover more details and has fewer artifacts. In addition, from the spectral correlation curve, our proposed method also achieves higher spectral accuracy than existing methods.

Figure 7.Reconstruction results of GAP-CCoT and other spectral reconstruction algorithms ( $λ$ -net, TSA-net, GAP-net, DGSMP, PnP-DIP-HSI) in two real scenes (scene 1 and scene 2).

5. CONCLUSION AND DISCUSSION

In this paper, we use the inductive bias ability of convolution and the powerful modeling ability of Transformer to propose a parallel module, named CCoT, which can obtain more effective spectral features. We integrate this module with a physics-driven deep unfolding idea and GAP algorithm, which can be well applied to SCI reconstruction.

Figure 8.Reconstructed frame of our method and other algorithms (GAP-TV, DeSCI, PnP-FFDNet, U-net, BIRNAT, RevSCI) on six benchmark datasets.

During the review of our paper, we did notice that several new algorithms were proposed for spectral SCI reconstruction [35,93 –96]. One of them used Transformer and brought competitive results to ours [93].

Regarding future work, advances in deep learning have empowered computational imaging for practical applications. Most recently, Transformer has shown promising performance on many vision problems mainly because of its strong capability of extracting features. The self-attention mechanism in Transformer can capture global interactions between contexts and thus has advantages for global and local, muti-scale, spatial–temporal, or other features extraction that is difficult to realize by normal CNN-based networks. This can also inspire us to design new computational imaging systems. Specifically, the sampling process should be able to play the role of the first layer in Transformer to extract global or local features of the desired scene.

Acknowledgment

Acknowledgment. Zongliang Wu and Xin Yuan acknowledge the Research Center for Industries of the Future (RCIF) at Westlake University, the Westlake Foundation for supporting this work, and the funding from Lochn Optics.

References

[1] Z. Meng, M. Qiao, J. Ma, Z. Yu, K. Xu, X. Yuan. Snapshot multispectral endomicroscopy. Opt. Lett., 45, 3897-3900(2020).

[2] Y.-Z. Feng, D.-W. Sun. Application of hyperspectral imaging in food safety inspection and control: a review. Crit. Rev. Food Sci. Nutr., 52, 1039-1058(2012).

[3] J. M. Bioucas-Dias, A. Plaza, G. Camps-Valls, P. Scheunders, N. Nasrabadi, J. Chanussot. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag., 1, 6-36(2013).

[4] A. Wagadarikar, R. John, R. Willett, D. Brady. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt., 47, B44-B51(2008).

[5] M. E. Gehm, R. John, D. J. Brady, R. M. Willett, T. J. Schulz. Single-shot compressive spectral imaging with a dual-disperser architecture. Opt Express, 15, 14013-14027(2007).

[6] J. M. Bioucas-Dias, M. A. T. Figueiredo. A new TwIST: two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process., 16, 2992-3004(2007).

[7] X. Yuan. Generalized alternating projection based total variation minimization for compressive sensing. IEEE International Conference on Image Processing (ICIP), 2539-2543(2016).

[8] Y. Liu, X. Yuan, J. Suo, D. J. Brady, Q. Dai. Rank minimization for snapshot compressive imaging. IEEE Trans. Pattern Anal. Mach. Intell., 41, 2990-3006(2018).

[9] X. Miao, X. Yuan, Y. Pu, V. Athitsos. λ-net: reconstruct hyperspectral images from a snapshot measurement. IEEE/CVF International Conference on Computer Vision, 4059-4069(2019).

[10] J. Wang, Y. Zhang, X. Yuan, Y. Fu, Z. Tao. A new backbone for hyperspectral image reconstruction(2021).

[11] G. Barbastathis, A. Ozcan, G. Situ. On the use of deep learning for computational imaging. Optica, 6, 921-943(2019).

[12] Y. Fu, T. Zhang, L. Wang, H. Huang. Coded hyperspectral image reconstruction using deep external and internal learning. IEEE Trans. Pattern Anal. Mach. Intell., 44, 3404-3420(2021).

[13] Y. Pu, D. Lee, M. Sugiyama, Z. Gan, U. Luxburg, R. Henao, I. Guyon, X. Yuan, C. Li, R. Garnett, A. Stevens, L. Carin. Variational autoencoder for deep learning of images, labels and captions. Advances in Neural Information Processing Systems, 29(2016).

[14] X. Yuan, D. J. Brady, A. K. Katsaggelos. Snapshot compressive imaging: theory, algorithms, and applications. IEEE Signal Process Mag., 38, 65-88(2021).

[15] K. Gregor, Y. LeCun. Learning fast approximations of sparse coding. 27th International Conference on Machine Learning, 399-406(2010).

[16] Y. Yang, J. Sun, H. Li, Z. Xu. Deep ADMM-Net for compressive sensing MRI. 30th International Conference on Neural Information Processing Systems, 10-18(2016).

[17] Y. Yang, J. Sun, H. Li, Z. Xu. ADMM-CSNet: a deep learning approach for image compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell., 42, 521-538(2018).

[18] J. Zhang, B. Ghanem. ISTA-Net: interpretable optimization-inspired deep network for image compressive sensing. IEEE Conference on Computer Vision and Pattern Recognition, 1828-1837(2018).

[19] L. Wang, C. Sun, Y. Fu, M. H. Kim, H. Huang. Hyperspectral image reconstruction using a deep spatial-spectral prior. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8032-8041(2019).

[20] Z. Meng, S. Jalali, X. Yuan. GAP-Net for snapshot compressive imaging(2020).

[21] O. Ronneberger, P. Fischer, T. Brox. U-Net: convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-assisted Intervention, 234-241(2015).

[22] K. Han, Y. Wang, H. Chen, X. Chen, J. Guo, Z. Liu, Y. Tang, A. Xiao, C. Xu, Y. Xu. A survey on visual transformer(2020).

[23] Z. Meng, Z. Yu, K. Xu, X. Yuan. Self-supervised neural networks for spectral snapshot compressive imaging. IEEE/CVF International Conference on Computer Vision, 2622-2631(2021).

[24] T. Huang, W. Dong, X. Yuan, J. Wu, G. Shi. Deep Gaussian scale mixture prior for spectral compressive imaging. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 16216-16225(2021).

[25] D. Donoho. Compressed sensing. IEEE Trans. Inf. Theory, 52, 1289-1306(2006).

[26] E. J. Candès, J. Romberg, T. Tao. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory, 52, 489-509(2006).

[27] P. Llull, X. Liao, X. Yuan, J. Yang, D. Kittle, L. Carin, G. Sapiro, D. J. Brady. Coded aperture compressive temporal imaging. Opt Express, 21, 10526-10545(2013).

[28] Y. Hitomi, J. Gu, M. Gupta, T. Mitsunaga, S. K. Nayar. Video from a single coded exposure photograph using a learned over-complete dictionary. International Conference on Computer Vision, 287-294(2011).

[29] D. Reddy, A. Veeraraghavan, R. Chellappa. P2C2: programmable pixel compressive camera for high speed imaging. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 329-336(2011).

[30] M. A. T. Figueiredo, R. D. Nowak, S. J. Wright. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process., 1, 586-597(2007).

[31] M. Aharon, M. Elad, A. Bruckstein. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process., 54, 4311-4322(2006).

[32] X. Yuan, T.-H. Tsai, R. Zhu, P. Llull, D. Brady, L. Carin. Compressive hyperspectral imaging with side information. IEEE J. Sel. Top. Signal Process., 9, 964-976(2015).

[33] W. He, N. Yokoya, X. Yuan. Fast hyperspectral image recovery of dual-camera compressive hyperspectral imaging via non-iterative subspace-based fusion. IEEE Trans. Image Process., 30, 7170-7183(2021).

[34] J. Yang, X. Liao, X. Yuan, P. Llull, D. J. Brady, G. Sapiro, L. Carin. Compressive sensing by learning a Gaussian mixture model from measurements. IEEE Trans. Image Process., 24, 106-119(2015).

[35] Z. Cheng, B. Chen, R. Lu, Z. Wang, H. Zhang, Z. Meng, X. Yuan. Recurrent neural networks for snapshot compressive imaging. IEEE Trans. Pattern Anal. Mach. Intell.(2022).

[36] S. Zheng, Y. Liu, Z. Meng, M. Qiao, Z. Tong, X. Yang, S. Han, X. Yuan. Deep plug-and-play priors for spectral snapshot compressive imaging. Photon. Res., 9, B18-B29(2021).

[37] Z. Lai, K. Wei, Y. Fu. Deep plug-and-play prior for hyperspectral image restoration. Neurocomputing, 481, 281-293(2022).

[38] S. Boyd, N. Parikh, E. Chu. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers(2011).

[39] Y. LeCun, Y. Bengio. Convolutional networks for images, speech, and time series. The Handbook of Brain Theory and Neural Networks, 255-258(1998).

[40] A. Krizhevsky, I. Sutskever, G. E. Hinton. ImageNet classification with deep convolutional neural networks. Advances Information Processing Systems 25, 1097-1105(2012).

[41] K. He, X. Zhang, S. Ren, J. Sun. Deep residual learning for image recognition. IEEE Conference on Computer Vision and Pattern Recognition, 770-778(2016).

[42] G. Huang, Z. Liu, L. Van Der Maaten, K. Q. Weinberger. Densely connected convolutional networks. IEEE Conference on Computer Vision and Pattern Recognition, 4700-4708(2017).

[43] J. Redmon, S. Divvala, R. Girshick, A. Farhadi. You only look once: unified, real-time object detection. IEEE Conference on Computer Vision and Pattern Recognition, 779-788(2016).

[44] J. Long, E. Shelhamer, T. Darrell. Fully convolutional networks for semantic segmentation. IEEE Conference on Computer Vision and Pattern Recognition, 3431-3440(2015).

[45] C. Tian, L. Fei, W. Zheng, Y. Xu, W. Zuo, C.-W. Lin. Deep learning on image denoising: an overview. Neural Netw., 131, 251-275(2020).

[46] R. Stone. CenterTrack: an IP overlay network for tracking DoS floods. USENIX Security Symposium, 21, 114(2000).

[47] L. He, X. Liao, W. Liu, X. Liu, P. Cheng, T. Mei. FastReID: a PyTorch toolbox for general instance re-identification(2020).

[48] J. Hu, L. Shen, G. Sun. Squeeze-and-excitation networks. IEEE Conference on Computer Vision and Pattern Recognition, 7132-7141(2018).

[49] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, I. Polosukhin. Attention is all you need. Advances in Neural Information Processing Systems, 5998-6008(2017).

[50] A. Dosovitskiy, L. Beyer, A. Kolesnikov, D. Weissenborn, X. Zhai, T. Unterthiner, M. Dehghani, M. Minderer, G. Heigold, S. Gelly. An image is worth 16 × 16 words: transformers for image recognition at scale(2020).

[51] X. Zhu, W. Su, L. Lu, B. Li, X. Wang, J. Dai. Deformable DETR: deformable transformers for end-to-end object detection. International Conference on Learning Representations, 1-16(2020).

[52] X. Dong, J. Bao, D. Chen, W. Zhang, N. Yu, L. Yuan, D. Chen, B. Guo. CSWin transformer: a general vision transformer backbone with cross-shaped windows(2021).

[53] H. Touvron, M. Cord, M. Douze, F. Massa, A. Sablayrolles, H. Jégou. Training data-efficient image Transformers & distillation through attention. International Conference on Machine Learning (PMLR), 10347-10357(2021).

[54] L. Yuan, Y. Chen, T. Wang, W. Yu, Y. Shi, F. E. H. Tay, J. Feng, S. Yan. Tokens-to-token ViT: training vision Transformers from scratch on imageNet. IEEE International Conference on Computer Vision, 558-567(2021).

[55] C. Sun, A. Shrivastava, S. Singh, A. Gupta. Revisiting unreasonable effectiveness of data in deep learning era. IEEE International Conference on Computer Vision, 843-852(2017).

[56] Z. Liu, Y. Lin, Y. Cao, H. Hu, Y. Wei, Z. Zhang, S. Lin, B. Guo. Swin Transformer: hierarchical vision Transformer using shifted windows(2021).

[57] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, L. Fei-Fei. ImageNet: a large-scale hierarchical image database. IEEE Conference on Computer Vision and Pattern Recognition, 248-255(2009).

[58] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollár, C. L. Zitnick. Microsoft COCO: common objects in context. European Conference on Computer Vision, 740-755(2014).

[59] B. Zhou, H. Zhao, X. Puig, S. Fidler, A. Barriuso, A. Torralba. Scene parsing through ADE20K dataset. IEEE Conference on Computer Vision and Pattern Recognition, 633-641(2017).

[60] B. Zhou, H. Zhao, X. Puig, T. Xiao, S. Fidler, A. Barriuso, A. Torralba. Semantic understanding of scenes through the ADE20K dataset. Int. J. Comput. Vis., 127, 302-321(2019).

[61] J. Liang, J. Cao, G. Sun, K. Zhang, L. Van Gool, R. Timofte. SwinIR: image restoration using Swin Transformer. IEEE/CVF International Conference on Computer Vision, 1833-1844(2021).

[62] Y. Li, T. Yao, Y. Pan, T. Mei. Contextual Transformer networks for visual recognition(2021).

[63] Z. Peng, W. Huang, S. Gu, L. Xie, Y. Wang, J. Jiao, Q. Ye. Conformer: local features coupling global representations for visual recognition(2021).

[64] J. R. Hershey, J. L. Roux, F. Weninger. Deep unfolding: model-based inspiration of novel deep architectures(2014).

[65] X. Liao, H. Li, L. Carin. Generalized alternating projection for weighted-l_2,1 minimization with applications to model-based compressive sensing. SIAM J. Imag. Sci., 7, 797-823(2014).

[66] B. Xu, N. Wang, T. Chen, M. Li. Empirical evaluation of rectified activations in convolutional network(2015).

[67] W. Shi, J. Caballero, F. Huszár, J. Totz, A. P. Aitken, R. Bishop, D. Rueckert, Z. Wang. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. IEEE Conference on Computer Vision and Pattern Recognition, 1874-1883(2016).

[68] Z. Wang, A. C. Bovik, H. R. Sheikh, E. P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process., 13, 600-612(2004).

[69] F. Yasuma, T. Mitsunaga, D. Iso, S. K. Nayar. Generalized assorted pixel camera: postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process., 19, 2241-2253(2010).

[70] I. Choi, D. S. Jeon, G. Nam, D. Gutierrez, M. H. Kim. High-quality hyperspectral reconstruction using a spectral prior. ACM Trans. Graph., 36, 218(2017).

[71] Z. Meng, J. Ma, X. Yuan. End-to-end low cost compressive spectral imaging with spatial-spectral self-attention. European Conference on Computer Vision, 187-204(2020).

[72] D. P. Kingma, J. Ba. ADAM: a method for stochastic optimization(2014).

[73] X. Yuan, P. Llull, X. Liao, J. Yang, D. J. Brady, G. Sapiro, L. Carin. Low-cost compressive sensing for color video and depth. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 3318-3325(2014).

[74] X. Yuan, Y. Liu, J. Suo, Q. Dai. Plug-and-play algorithms for large-scale snapshot compressive imaging. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 1447-1457(2020).

[75] Z. Cheng, R. Lu, Z. Wang, H. Zhang, B. Chen, Z. Meng, X. Yuan. BIRNAT: bidirectional recurrent neural networks with adversarial training for video snapshot compressive imaging. European Conference on Computer Vision, 258-275(2020).

[76] M. Qiao, Z. Meng, J. Ma, X. Yuan. Deep learning for video compressive sensing. APL Photon., 5, 30801(2020).

[77] Z. Wang, H. Zhang, Z. Cheng, B. Chen, X. Yuan. MetaSCI: scalable and adaptive reconstruction for video compressive sensing. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2083-2092(2021).

[78] Z. Cheng, B. Chen, G. Liu, H. Zhang, R. Lu, Z. Wang, X. Yuan. Memory-efficient network for large-scale video compressive sensing. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 16246-16255(2021).

[79] Y. Sun, X. Yuan, S. Pang. High-speed compressive range imaging based on active illumination. Opt. Express, 24, 22836-22846(2016).

[80] Y. Sun, X. Yuan, S. Pang. Compressive high-speed stereo imaging. Opt. Express, 25, 18182-18190(2017).

[81] X. Yuan, Y. Pu. Parallel lensless compressive imaging via deep convolutional neural networks. Opt. Express, 26, 1962-1977(2018).

[82] T.-H. Tsai, X. Yuan, D. J. Brady. Spatial light modulator based color polarization imaging. Opt. Express, 23, 11912-11926(2015).

[83] M. Qiao, X. Liu, X. Yuan. Snapshot spatial–temporal compressive imaging. Opt. Lett., 45, 1659-1662(2020).

[84] R. Lu, B. Chen, G. Liu, Z. Cheng, M. Qiao, X. Yuan. Dual-view snapshot compressive imaging via optical flow aided recurrent neural network. Int. J. Comput. Vis., 129, 3279-3298(2021).

[85] Y. Xue, S. Zheng, W. Tahir, Z. Wang, H. Zhang, Z. Meng, L. Tian, X. Yuan. Block modulating video compression: an ultra low complexity image compression encoder for resource limited platforms(2022).

[86] B. Zhang, X. Yuan, C. Deng, Z. Zhang, J. Suo, Q. Dai. End-to-end snapshot compressed super-resolution imaging with deep optics. Optica, 9, 451-454(2022).

[87] Z. Chen, S. Zheng, Z. Tong, X. Yuan. Physics-driven deep-learning enables temporal compressive coherent diffraction imaging. Optica, 9, 677-680(2022).

[88] T.-H. Tsai, P. Llull, X. Yuan, D. J. Brady, L. Carin. Spectral-temporal compressive imaging. Opt. Lett., 40, 4054-4057(2015).

[89] M. Qiao, Y. Sun, J. Ma, Z. Meng, X. Liu, X. Yuan. Snapshot coherence tomographic imaging. IEEE Trans. Comput. Imaging, 7, 624-637(2021).

[90] X. Yuan. Compressive dynamic range imaging via Bayesian shrinkage dictionary learning. Opt. Eng., 55, 123110(2016).

[91] X. Yuan, X. Liao, P. Llull, D. Brady, L. Carin. Efficient patch-based approach for compressive depth imaging. Appl. Opt., 55, 7556-7564(2016).

[92] X. Ma, X. Yuan, C. Fu, G. R. Arce. LED-based compressive spectral-temporal imaging. Opt. Express, 29, 10698-10715(2021).

[93] Y. Cai, J. Lin, X. Hu, H. Wang, X. Yuan, Y. Zhang, R. Timofte, L. Van Gool. Mask-guided spectral-wise Transformer for efficient hyperspectral image reconstruction(2022).

[94] J. Lin, Y. Cai, X. Hu, H. Wang, X. Yuan, Y. Zhang, R. Timofte, L. Van Gool. Coarse-to-fine sparse Transformer for hyperspectral image reconstruction(2022).

[95] X. Hu, Y. Cai, J. Lin, H. Wang, X. Yuan, Y. Zhang, R. Timofte, L. Van Gool. HDNet: high-resolution dual-domain learning for spectral compressive imaging. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 17542-17551(2022).

[96] J. Wang, Y. Zhang, X. Yuan, Z. Meng, Z. Tao. Modeling mask uncertainty in hyperspectral image reconstruction(2021).