- Photonics Research
- Vol. 9, Issue 4, 643 (2021)
Abstract
1. INTRODUCTION
In recent years, considerable effort has been devoted to the investigation of optical solitary waves [1] due to their fundamental impact on nonlinear wave propagation, spawning exciting applications along the way such as supercontinuum light sources [2], soliton lasers [3], and an improved understanding of the development and control of rogue waves (RWs) [4]. A special type of solitary waves, the RW phenomenon, which was first observed in the ocean, is a rare, short-lived, and high-energy event with amplitude much higher than the average wave crests around it [5]. The typical feature of RWs is that they suddenly appear and increase up to a very high and abnormal amplitude to finally disappear without a trace [6,7]. The experimental observation and theoretical analysis of RWs have ranged from Bose–Einstein condensates (BECs) [8,9] to optical systems [10–12], oceans [13], superfluids [14], and plasmas [15,16]; see more details in two recent review articles [17,18]. One possible mathematical model to describe such RWs is the rational solution of one-dimensional nonlinear Schrödinger (NLS) type equations. Moreover, research has diversified, also addressing optical solitary waves in higher-dimensional media, which display a more complex phenomenology due to the increased degrees of freedom [19].
In this context, the formation of self-trapped wave packets or light bullets, is one of the most exciting yet experimentally unsolved problems in optics [20,21]. Light bullets are spatiotemporal solitons that form when a suitable nonlinearity arrests both spatial diffraction and temporal group-velocity dispersion. Despite considerable theoretical work, experimental research on light bullets is rare, and one of the main reasons is that in nonlinear propagation, three-dimensional light bullets tend to disintegrate due to inherent instabilities. However, different situations are found in BECs and nonlinear optics with temporally or spatially modulated parameters. In particular, it was shown in Ref. [22] that complete stabilization of a cylindrical (2+1)-dimensional [(2+1)D] spatial soliton can be secured in a layered medium with nonlinearity management. A scheme for stabilizing spatiotemporal solitons in media with cubic self-focusing nonlinearity and dispersion management was proposed in Ref. [23]. The formation of tandem structures, which are composed of periodically alternating linear dispersive and nonlinear layers, was studied in Refs. [24,25]. Moreover, alteration of atomic scattering length achieved by Feshbach resonance has been used to dynamically stabilize higher-dimensional bright solitons [26]. Thus, the study of the (2+1)D and (3+1)D variable coefficients NLS equations (NLSEs) has recently been one of the central issues in the field of nonlinear optics. One of the interesting challenges concerns how to characterize the nonlinear light bullets on analytical level [27–29]. In general, the analytical study of the multidimensional light bullets is impeded by the lack of the corresponding integrable systems. Therefore, several approaches have been recently developed to overcome this limitation. The traveling wave and light bullet soliton solutions to the generalized NLSE in (3+1)D for a cubic nonlinearity were first developed in Ref. [30] for anomalous dispersion and were generalized in Ref. [31] for normal dispersion by using the F-expansion technique. Exact solutions for varying potential and nonlinearity were found in Ref. [32] by similarity transformations. Nonautonomous rogue wave solutions have also been found for the generalized NLSEs with variable coefficients in three-dimensional spaces [33] based on the similarity analysis idea.
Very recently, the spatiotemporal dynamics of RW solutions in a composite (2+1)D were investigated in Ref. [34]. A novel type of light bullets, which take the shape of RWs and travel on a finite (2+1)D space-time background, has been obtained. It was shown that both the fundamental and second-order RWs have a directional preference or a bullet nature that can propagate in a certain direction with transverse double localization. Such special (2+1)D RW behavior has been called rogue wave bullets. We shall in this paper proceed along this direction to get rogue wave bullets of a new inhomogeneous (3+1)D integrable system where coefficients depend on time and transverse radial coordinates. The main result of the present work is the possibility to obtain a single optical sphere and homocentric optical spheres for an inhomogeneous (3+1)D NLSE with spherical symmetry.
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
2. THE THREE-DIMENSIONAL ROGUE WAVE LIGHT BULLETS
The three-dimensional inhomogeneous NLSE with variable coefficients can be written in a dimensionless form:
According to the above transformation defined by Eqs. (2), (4), and (5), we set , and then Eq. (1) leads to a solvable three-dimensional inhomogeneous NLSE with spatial nonlinearities:
In optics, spatially inhomogeneous nonlinearities can be realized in various ways [41]. In a BEC, Eq. (6) describes the evolution of matter waves, where the spatially modulated nonlinearity landscape can be generated by the Feshbach resonance in nonuniform external fields [42,43]. Nonlinearity can also be modulated in optical structures, e.g., in photonic crystal fibers with the holes infiltrated with a highly nonlinear material, for example, index-matching nonlinear liquids [44,45].
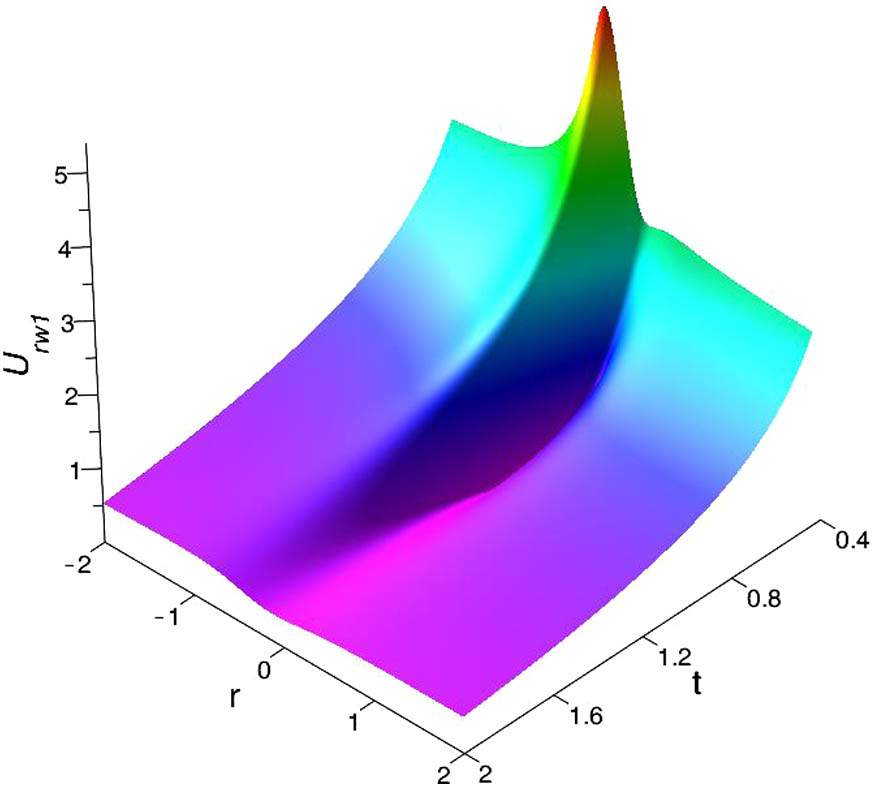
Figure 1.Evolution of
![]()
Figure 2.Profiles of
We next investigate the features of the amplitude of the 3D RW solution from Eq. (7). Indeed, there exists a critical point such that oscillates with respect to when , but it is a monotonic function of when .
![]()
Figure 3.Profiles of
The radius of these spheres increases to a certain value and then reaches an upper limit, which corresponds to localized feature of the rogue wave. In this process, the radius of the sphere may have oscillation. Equivalently, is not a monotonic function of time , although it is bounded. In other words, the isosurface of forms size-bounded sphere, which is a strong reflection of the localized nature of rogue waves in three dimensions. Moreover, the polynomial form of the rogue wave in the one-dimensional NLSE is reflected by the oscillation of the radius of the isosurface. Therefore, the behavior of the sphere of the isosurface represents the nature of the first-order rogue wave of the NLSE: polynomial and having a doubly localized property. The asymptotical radius of the isosurface valued at is given by .
![]()
Figure 4.Radius of the sphere for the isosurface given by
![]()
Figure 5.Localized profiles of the
![]()
Figure 6.Profiles of
3. THE STABILITY OF THE OPTICAL SPHERE SOLUTIONS
![]()
Figure 7.(a) Growth rates
4. CONCLUSION
In conclusion, we have shown that in the (3+1)-dimensional NLSE with varying coefficients, localized solutions in the form of rational formulas can exist owing to a specific transformation that allows us to reduce the dimensionality of the equation from (3+1) dimensions to (1+1) dimensions. These solutions are localized both in space and in time, and thus their corresponding isosurfaces are single spheres or homocentric spheres, which oscillate along the radius direction and are completely different from the well-known standard traveling light bullets. They can be interpreted as prototypes of RW light bullet solutions in the (3+1)-dimensional time-space. The other properties of the new nonautonomous RW light bullets have been studied analytically. Our analytical findings are confirmed by numerical plots of these solutions. A linear stability analysis in terms of spherical harmonic modes has been investigated. We have found that the RW light bullet solutions are stable for higher modes and transversely unstable for lower modes of the perturbation. Experimental advances have recently provided a strong incentive in the area of RWs in complex media [54]. Note that a demonstration of the direct observation of RWs in self-excited 3D longitudinal plasma density waves was reported in Ref. [55] by using self-excited dust acoustic waves as a platform. We believe that the results obtained here can stimulate further research on the experiments and help to understand the behavior of 3D RWs in a wide range of nonlinear physical areas.
Acknowledgment
Acknowledgment. J. He gratefully acknowledges support from the University of Lille for his visit. C. G. L. Tiofack acknowledges support from the Ministry of Higher Education and Research, Hauts-de-France Council, and ERDF through the Contract de Projets Etat-Region (CPER Photonics for Society P4S). C. G. L. Tiofack and M. Taki appreciate helpful discussions with S. Coulibaly.
References
[1] Y. Kivshar, G. Agrawal. Optical Solitons(2003).
[2] R. Alfano. The Supercontinuum Laser Source: Fundamentals with Updated References(2006).
[3] L. F. Mollenauer, R. H. Stolen. The soliton laser. Opt. Lett., 9, 13-15(1984).
[4] D. Solli, C. Ropers, P. Koonath, B. Jalali. Optical rogue waves. Nature, 450, 1054-1057(2007).
[5] N. Akhmediev, A. Ankiewicz, J. M. Soto-Crespo. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E, 80, 026601(2009).
[6] N. Akhmediev, A. Ankiewicz, M. Taki. Waves that appear from nowhere and disappear without a trace. Phys. Lett. A, 373, 675-678(2009).
[7] D. Kedziora, A. Ankiewicz, N. Akhmediev. Circular rogue wave clusters. Phys. Rev. E, 84, 056611(2011).
[8] Y. V. Bludov, V. V. Konotop, N. Akhmediev. Matter rogue waves. Phys. Rev. A, 80, 033610(2009).
[9] Y. V. Bludov, V. V. Konotop, N. Akhmediev. Vector rogue waves in binary mixtures of Bose-Einstein condensates. Eur. Phys. J. Spec. Top., 185, 169-180(2010).
[10] A. Montina, U. Bortolozzo, S. Residori, F. T. Arecchi. Non-Gaussian statistics and extreme waves in a nonlinear optical cavity. Phys. Rev. Lett., 103, 173901(2009).
[11] R. Höhmann, U. Kuhl, H. J. Stöckmann, L. Kaplan, E. J. Heller. Freak waves in the linear regime: a microwave study. Phys. Rev. Lett., 104, 093901(2010).
[12] M. Onorato, S. Residori, U. Bortolozzo, A. Montinad, F. T. Arecchi. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep., 528, 47-89(2013).
[13] C. Kharif, E. Pelinovsky, A. Slunyaev. Rogue Waves in the Ocean(2009).
[14] A. N. Ganshin, V. B. Efimov, G. V. Kolmakov, L. P. Mezhov-Deglin, P. V. E. McClintock. Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett., 101, 065303(2008).
[15] W. M. Moslem. Langmuir rogue waves in electron-positron plasmas. Phys. Plasmas, 18, 032301(2011).
[16] H. Bailung, S. K. Sharma, Y. Nakamura. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett., 107, 255005(2011).
[17] J. M. Dudley, G. Genty, A. Mussot, A. Chabchoub, F. Dias. Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys., 1, 675-689(2019).
[18] Y. F. Song, Z. H. Wang, C. Wang, K. Panajotov, H. Zhang. Recent progress on optical rogue waves in fiber lasers: status, challenges, and perspectives. Adv. Photon., 2, 024001(2020).
[19] J. J. Rasmussen, K. Rypdal. Blow-up in nonlinear Schröedinger equations-I: a general review. Phys. Scr., 33, 481-497(1986).
[20] Y. Silberberg. Collapse of optical pulse. Opt. Lett., 15, 1282-1284(1990).
[21] B. A. Malomed, D. Mihalache, F. Wise, L. Torner. Spatiotemporal optical solitons. J. Opt. B, 7, R53-R72(2005).
[22] I. Towers, B. A. Malomed. Stable (2+1)-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity. J. Opt. Soc. Am. B, 19, 537-543(2002).
[23] M. Matuszewski, M. Trippenbach, B. A. Malomed, E. Infeld, A. A. Skorupski. Two-dimensional dispersion-managed light bullets in Kerr media. Phys. Rev. E, 70, 016603(2004).
[24] L. Torner, S. Carrasco, J. P. Torres, L.-C. Crasovan, D. Mihalache. Tandem light bullets. Opt. Commun., 199, 277-281(2001).
[25] L. Torner, Y. V. Kartashov. Light bullets in optical tandems. Opt. Lett., 34, 1129-1131(2009).
[26] H. Saito, M. Ueda. Dynamically stabilized bright solitons in a two-dimensional Bose-Einstein condensate. Phys. Rev. Lett., 90, 040403(2003).
[27] K. D. Moll, A. L. Gaeta, G. Fibich. Self-similar optical wave collapse: observation of the Townes profile. Phys. Rev. Lett., 90, 203902(2003).
[28] W. P. Zhong, M. Belic, G. Assanto, B. A. Malomed, T. Huang. Light bullets in the spatiotemporal nonlinear Schrodinger equation with a variable negative diffraction coefficient. Phys. Rev. A, 84, 043801(2011).
[29] A. L. Gaeta. Optics. Collapsing light really shines. Science, 301, 54-55(2003).
[30] M. Belic, N. Petrovic, W. P. Zhong, R. H. Xie, G. Chen. Analytical light bullet solutions to the generalized (3 + 1)-dimensional nonlinear Schrodinger equation. Phys. Rev. Lett., 101, 123904(2008).
[31] N. Petrovic, M. Belic, W. P. Zhong, R. H. Xie, G. Chen. Exact spatiotemporal wave and soliton solutions to the generalized (3 + 1)-dimensional Schrödinger equation for both normal and anomalous dispersion. Opt. Lett., 34, 1609-1611(2009).
[32] Z. Y. Yan, V. V. Konotop. Exact solutions to three-dimensional generalized nonlinear Schrödinger equations with varying potential and nonlinearities. Phys. Rev. E, 80, 036607(2009).
[33] Z. Y. Yan, V. V. Konotop, N. Akhmediev. Three-dimensional rogue waves in nonstationary parabolic potentials. Phys. Rev. E, 82, 036610(2010).
[34] S. Chen, J. M. Soto-Crespo, F. Baronio, P. Grelu, D. Mihalache. Rogue-wave bullets in a composite (2+1)D nonlinear medium. Opt. Express, 24, 15251-15260(2016).
[35] L. Pitaevskii, S. Stringari. Bose-Einstein Condensation(2003).
[36] Z. Y. Yan, C. Hang. Analytical three-dimensional bright solitons and soliton pairs in Bose-Einstein condensates with time-space modulation. Phys. Rev. A, 80, 063626(2009).
[37] F. Dalfovo, S. Giorgini, L. P. Pitaevskii, S. Stringari. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys., 71, 463-512(1999).
[38] J. Belmonte-Beitia, V. M. Perez-Garcia, V. Vekslerchik, P. J. Torres. Lie symmetries and solitons in nonlinear systems with spatially inhomogeneous nonlinearities. Phys. Rev. Lett., 98, 064102(2007).
[39] J. S. He, Y. Li. Designable integrability of the variable coefficient nonlinear Schrodinger equations. Stud. Appl. Math., 126, 1-15(2010).
[40] Y. Y. Wang, J. S. He, Y. S. Li. Soliton and rogue wave solution of the new nonautonomous nonlinear Schrödinger equation. Commun. Theor. Phys., 56, 995-1004(2011).
[41] Y. V. Kartashov, B. A. Malomed, L. Torner. Solitons in nonlinear lattices. Rev. Mod. Phys., 83, 247-305(2011).
[42] D. M. Bauer, M. Lettner, C. Vo, G. Rempe, S. Dürr. Control of a magnetic Feshbach resonance with laser light. Nat. Phys., 5, 339-342(2009).
[43] R. Yamazaki, S. Taie, S. Sugawa, Y. Takahashi. Submicron spatial modulation of an interatomic interaction in a Bose-Einstein condensate. Phys. Rev. Lett., 105, 050405(2010).
[44] A. Fuerbach, P. Steinvurzel, J. A. Bolger, A. Nulsen, B. J. Eggleton. Nonlinear propagation effects in antiresonant high-index inclusion photonic crystal fibers. Opt. Lett., 30, 830-832(2005).
[45] C. R. Rosberg, F. H. Bennet, D. N. Neshev, P. D. Rasmussen, O. Bang, W. Krolikowski, A. Bjarklev, Y. S. Kivshar. Tunable diffraction and self-defocusing in liquid-filled photonic crystal fibers. Opt. Express, 15, 12145-12150(2007).
[46] D. H. Peregrine. Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. B, 25, 16-43(1983).
[47] N. N. Akhmediev, V. M. Eleonskii, N. E. Kulagin. Generation of periodic trains of picoseconld pulses in an optical fiber: exact solutions. Z. Eksp. Teor. Fiz., 89, 1542-1551(1985).
[48] J. S. He, H. R. Zhang, L. H. Wang, K. Porsezian, A. S. Fokas. Generating mechanism for higher-order rogue waves. Phys. Rev. E, 87, 052914(2013).
[49] L. H. Wang, J. S. He, H. Xu, J. Wang, K. Porsezian. Generation of higher-order rogue waves from multibreathers by double degeneracy in an optical fiber. Phys. Rev. E, 95, 042217(2017).
[50] D. E. Edmundson. Unstable higher modes of a three-dimensional nonlinear Schrödinger equation. Phys. Rev. E, 55, 7636(1997).
[51] J. M. Soto-Crespo, D. R. Heatley, E. M. Wright. Stability of the higher-bound states in a saturable self-focusing medium. Phys. Rev. E, 44, 636-644(1991).
[52] W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling. Numerical Recipes(1986).
[53] R. Driven, Y. V. Kartashov, B. A. Malomed, T. Meier, L. Torner. Three-dimensional hybrid vortex solitons. New J. Phys., 16, 063035(2014).
[54] M. Leonetti, C. Conti. Observation of three dimensional optical rogue waves through obstacles. Appl. Phys. Lett., 106, 254103(2015).
[55] Y. Y. Tsai, J. Y. Tsai, I. Lin. Generation of acoustic rogue waves in dusty plasmas through three-dimensional particle focusing by distorted waveforms. Nat. Phys., 12, 573-577(2016).

Set citation alerts for the article
Please enter your email address



