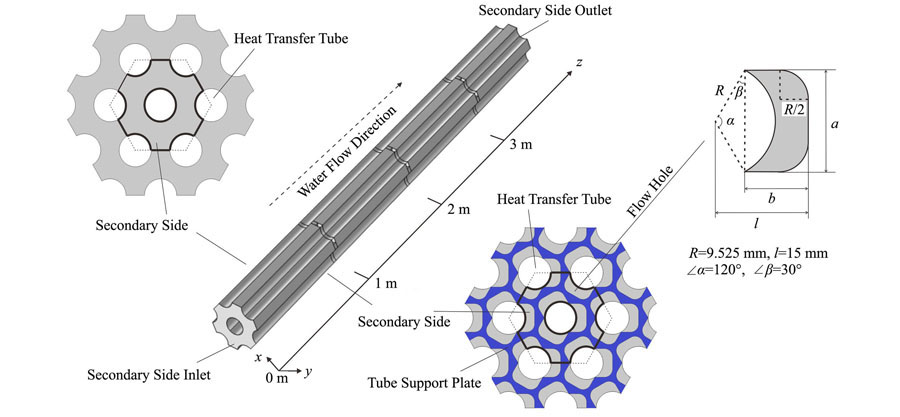
Faliang XIAO, Tingting ZHONG, Weiling FU, Xiaoyan KANG, Shuiquan DENG. Distribution of pH values in a model simulating the secondary side of a steam generator[J]. NUCLEAR TECHNIQUES, 2022, 45(11): 110602
Search by keywords or author
- NUCLEAR TECHNIQUES
- Vol. 45, Issue 11, 110602 (2022)
Abstract
Set citation alerts for the article
Please enter your email address



