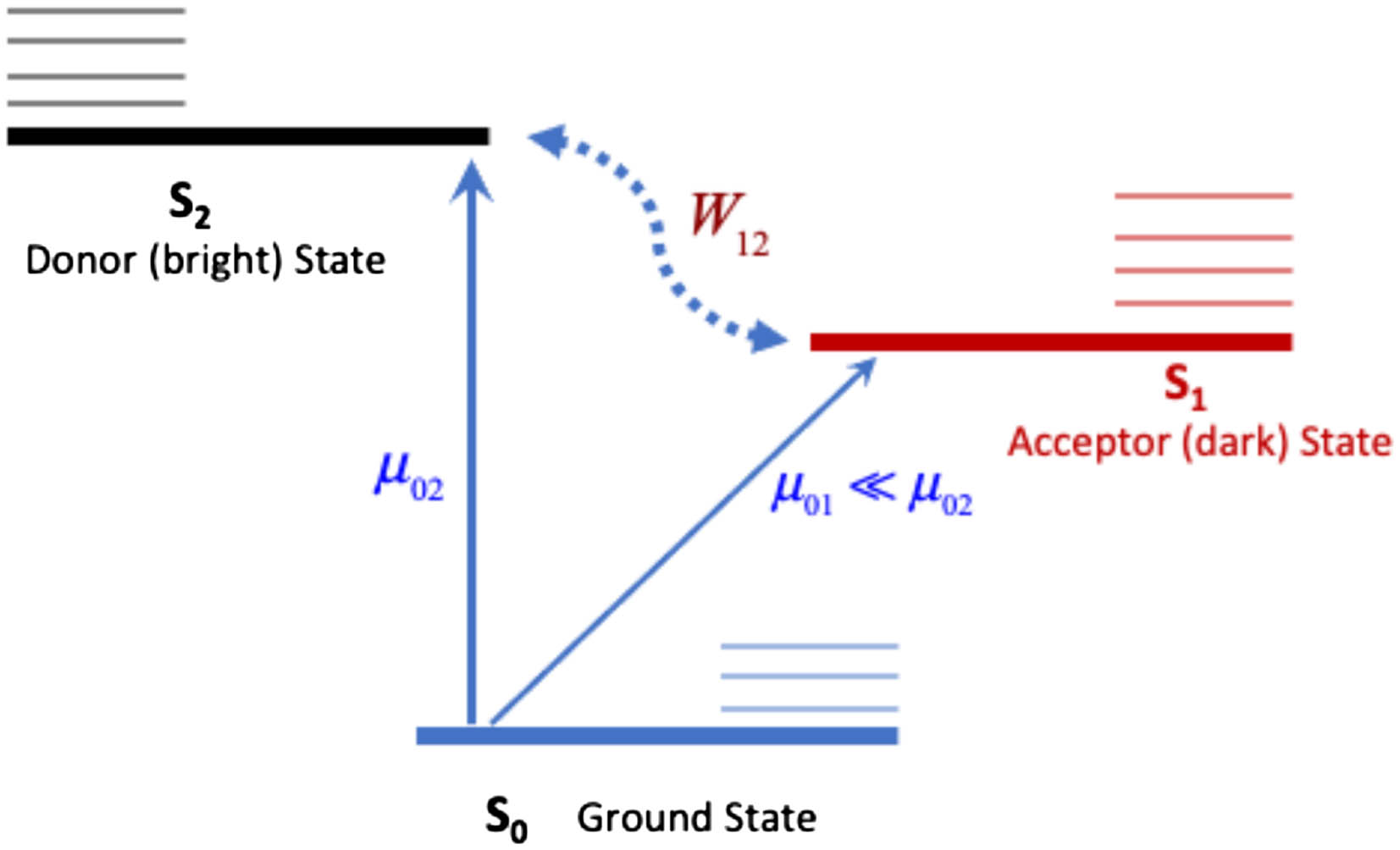
Fig. 1. Schematic view of the three-state model used for pyrazine. The ground state S₀ is indicated in thick solid blue line. The bright donor state S₂ is a thick solid black line, and the dark acceptor state S₂ is a thick solid red line. The thin horizontal lines are for the corresponding vibrational states. The interstate coupling W₁₂ in the dotted blue line and the transition dipole moments µ₀₁ and µ₀₂ are also indicated.

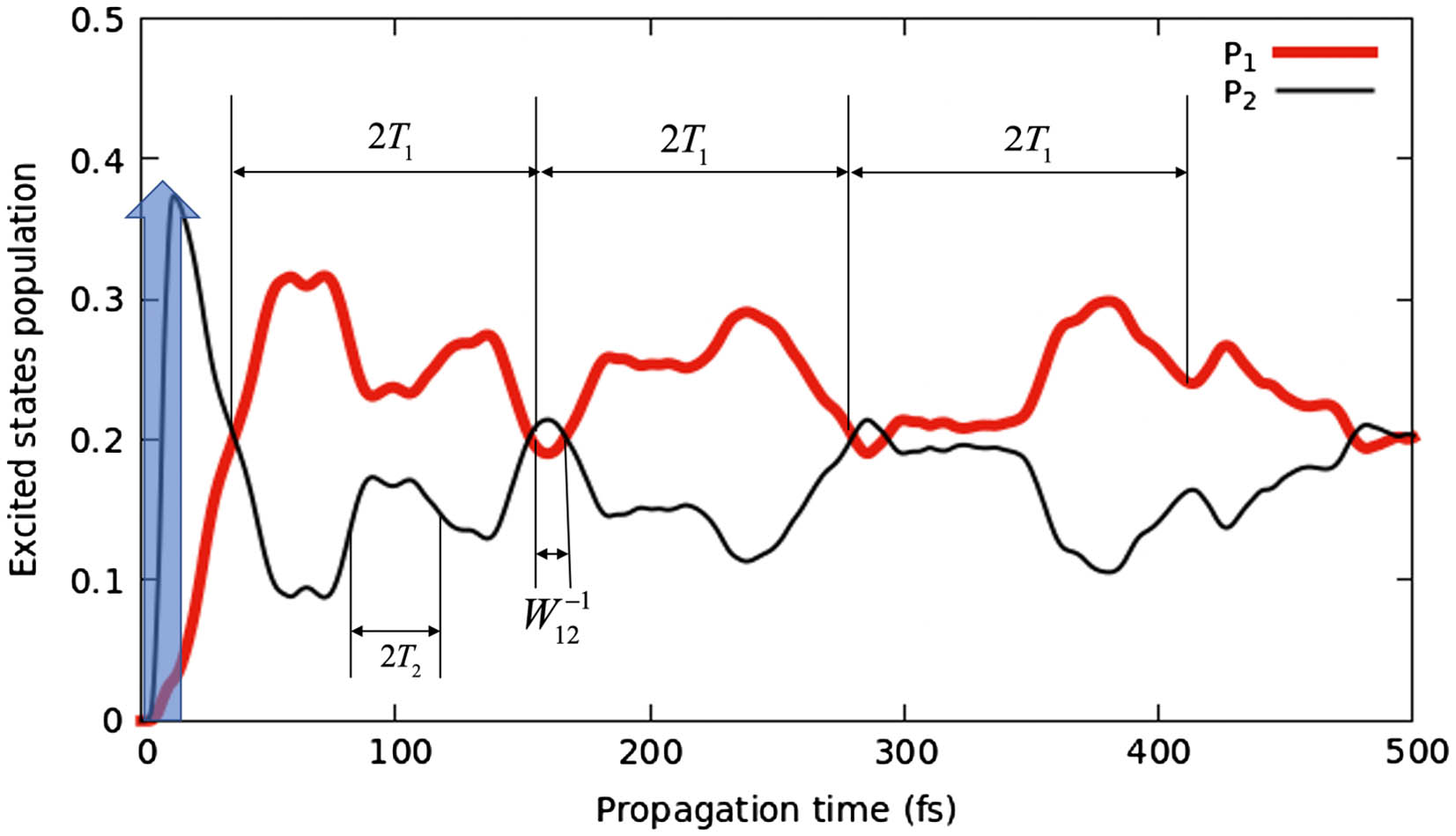
Fig. 2. Excited states populations as a function of propagation time in a minimal 2D model involving the CI branching space. P₂ and P₁ are, respectively, indicated by thin black and thick red solid lines. The blue vertical arrow at t = 0 symbolizes the vertical launching of the v = 0 wavepacket from the initial state S₀. T₁ and T₂ are, respectively, the vibrational periods of the excited states S₁ and S₂. W₁₂⁻¹ is a notation for the CI characteristic transfer time.

Fig. 3. Excited states populations as a function of propagation time in 4D (upper panel) and full 24D models (lower panel). Same notations as for Fig. 2.

Fig. 4. Sine-square laser electric field envelopes for two identical pulses as a function of time. The illustrated pulse duration corresponds to T = 14 fs, whereas the inter-pulse time delay is τ = 6 fs.

Fig. 5. Excited state population P₂ as a function of the leading intensity. Red dashed thin line for a single pulse, black thick solid line for two equal fluence pulses, with a delay of τ = 13 fs.

Fig. 6. Asymptotic contrast (4D) as a function of the inter-pulse delay τ for two pulses, each with a duration of T = 14 fs, equal fluence pulses of leading intensity I. The weak field regime is illustrated by the intensities I = 5 × 10¹² W/cm² in the blue dashed-dotted line, and by I = 10¹³ W/cm² in the red dashed line. I = 8.8 × 10¹³ W/cm² corresponds to the strong field regime, represented by the black solid curve.

Fig. 7. Excited states populations as a function of the propagation time for two pulses of intensity I = 10¹³ W/cm² delayed by τ = 25 fs. P₀ is indicated in the dashed-dotted black line, P₁ in the thick red solid line, and P₂ in the thin solid black line.

Fig. 8. Excited states populations as a function of the propagation time for two pulses of intensity I = 8.8 × 10¹³ W/cm² delayed by τ = 6 fs from a full 24D model. P₀ is indicated in the dashed-dotted black line, P₁ in the thick red solid line, and P₂ in the thin solid black line.

Fig. 9. Excited states populations as a function of the propagation time for two pulses of intensity I = 8.8 × 10¹³ W/cm² delayed by τ = 75 fs from a full 24D model. P₀ is indicated in the dashed-dotted black line, P₁ in the thick red solid line, and P₂ in the thin solid black line.

Fig. 10. Asymptotic contrast (4D) as a function of the inter-pulse delay τ for five equal kicks at a fixed intensity I = 5 × 10¹² W/cm². The thin black solid line is for kicks duration T = 10 fs; the thick red solid line is for T = 7 fs.

Fig. 11. Excited states populations as a function of the propagation time for five ultra-short T = 10 fs pulses of intensity I = 5 × 10¹² W/cm² delayed by τ = 13 fs for a full 24D model. P₀ is indicated in the dashed-dotted black line, P₁ in the thick red solid line, and P₂ in the thin solid black line.

Table 1. Number of Single-Particle Functions (n1⋯n8) Used for the Eight Combined Modes^a

Table 2. Contrasts for Several Excitation Frequencies for Both Mechanisms Discussed in the Text^a