- High Power Laser Science and Engineering
- Vol. 8, Issue 1, 010000e2 (2020)
Abstract
1 Introduction
The transport of high-current relativistic electron beams driven by ultraintense laser interactions with plasmas is relevant to many applications of high energy density physics, particularly in areas of the fast ignition scheme for inertial confinement fusion[
The transport of relativistic electrons can be inhibited by charge separation fields until a cold return current is generated or the electrons from ionization neutralize space charge fields. The transport of relativistic electrons through targets was found to be dependent on target materials, showing spatial disruption in insulators but more uniform propagation in metals[
In this paper, ultraintense laser-driven relativistic electron transport in a dielectric silicon (Si) target is studied. An ionization wave with a velocity less than the speed of light is observed by including the field ionization and collisional ionization processes. Widely spread ‘fountain’ electric fields associated with the sheath field occur during the relativistic electron propagation. In addition, two-stream instability (TSI) behind the ionization front arises when the relativistic electron current is sufficiently high. The structure of this paper is as follows. The ionization models (Section
Sign up for High Power Laser Science and Engineering TOC. Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
2 The ionization models
The 2D3V PIC simulation code EPOCH[
Since we focus on the relativistic electrons propagating through a high-density solid target that is strongly collisional, collisional ionization is also considered. The MBELL equation[
Note that the three-body recombination that is dependent on
3 The simulation model
To investigate the transport of relativistic electrons in insulators, the binary collision model of charged particles proposed by Sentoku et al.[
4 Results and discussions
4.1 Relativistic electron transport in a solid Si target
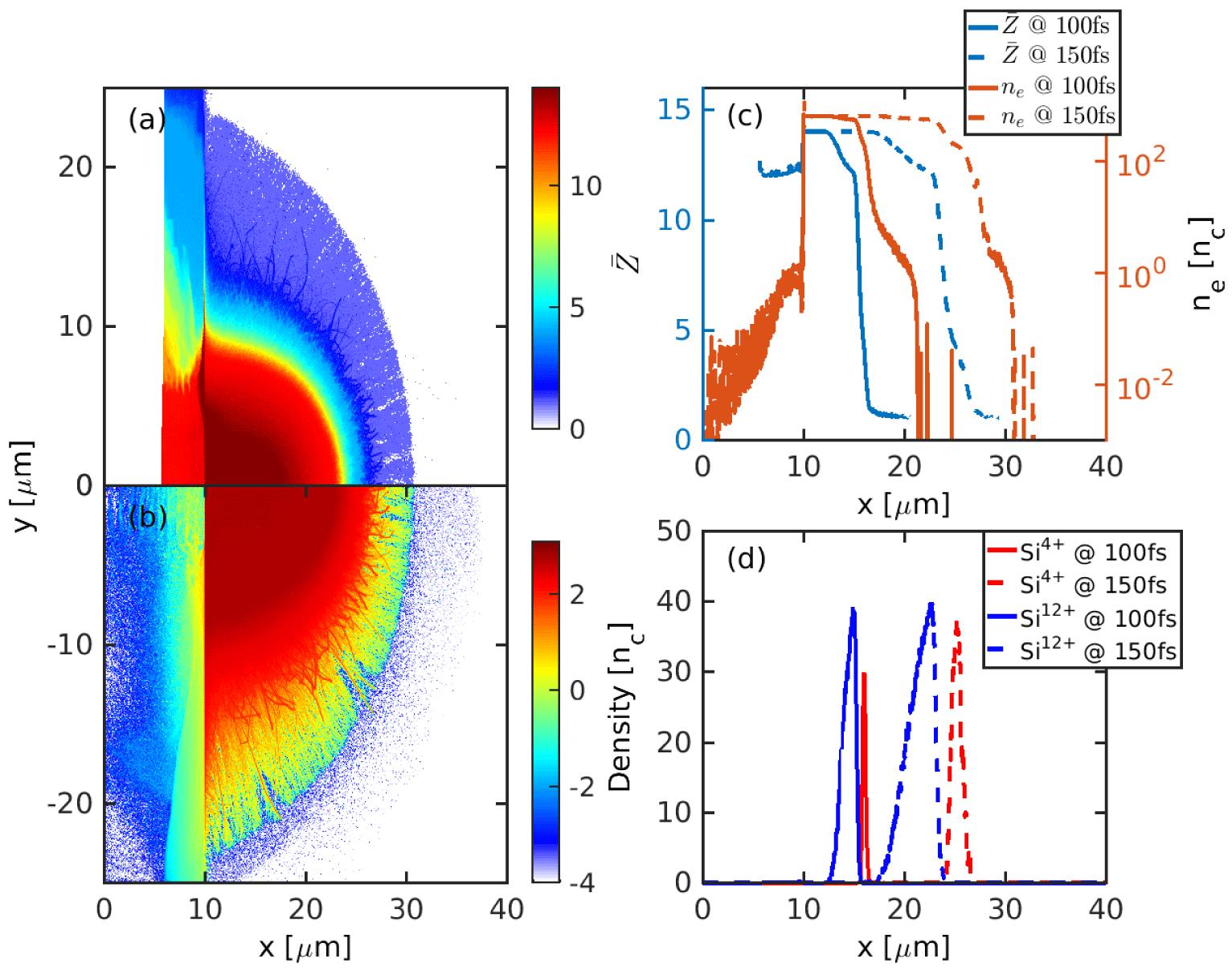
Figure
The self-generated magnetic field, longitudinal electrostatic field and transverse electrostatic field are shown in Figure
Initially, the laser pulse can penetrate the target before the ionization takes place, as shown in the transverse electric field distributions averaged over two laser cycles (Figure
The relativistic electrons are mainly accelerated by the
We now calculate the velocity of the ionization front using a reference frame co-moving with the ionization front. Assume that the velocity of the ionization front in the laboratory frame is
The sheath field in the ionization front reference is estimated by
Both magnetic and electric fields in the target show instabilities in Figure
4.2 Influence of laser intensity on the transport of ionization waves
To study the influence of laser intensity on the transport of the ionization wave, we vary the laser intensity while keeping other parameters the same as those in the above case. The profiles of average ionization degree and electron density along the laser propagation axis for different laser intensities are shown in Figure
The dependence of the ionization front velocity on laser intensity is presented in Figure
4.3 Relativistic electron transport in a plasma target without ionization
In order to make a comparison with the transport of relativistic electrons in the dielectric target, relativistic electron transport in a preionized Si target is also investigated. The target is composed of neutralized electrons and
5 Conclusion
In summary, ultraintense laser-driven relativistic electron transport in a dielectric Si target is studied using PIC simulations including the field and collisional ionization processes. An ionization wave propagating in the target is observed. In addition to the intense sheath fields (close to the threshold electric field of field ionization), a widely spread ‘fountain’ electric field occurs ahead due to the collective effect of free electrons and ions. The velocity of the ionization wave increases with laser intensity but is much less than the speed of light and also that from the 1D theoretical analysis, indicating that 2D3V numerical simulations are better to describe the relativistic electron transport in dielectric targets. The TSI behind the ionization front arises with increase in laser intensity. The results are useful for applications related to laser-driven relativistic electron transport in dielectric targets such as fast ignition and laser-driven ion acceleration.
References
[1] M. Tabak, J. Hammer, M. E. Glinsky, W. L. Kruer, S. C. Wilks, J. Woodworth, E. M. Campbell, M. D. Perry, R. J. Mason. Phys. Plasmas, 1, 1626(1994).
[2] A. Macchi, M. Borghesi, M. Passoni. Rev. Mod. Phys., 85, 751(2013).
[3] X. H. Yang, Y. Y. Ma, F. Q. Shao, H. Xu, M. Y. Yu, Y. Q. Gu, T. P. Yu, Y. Yin, C. L. Tian, S. Kawata. Laser Part. Beams, 28, 319(2010).
[4] Z. Jin, Z. L. Chen, H. B. Zhuo, A. Kon, M. Nakatsutsumi, H. B. Wang, B. H. Zhang, Y. Q. Gu, Y. C. Wu, B. Zhu, L. Wang, M. Y. Yu, Z. M. Sheng, R. Kodama. Phys. Rev. Lett., 107(2011).
[5] H. Chen, F. Fiuza, A. Link, A. Hazi, M. Hill, D. Hoarty, S. James, S. Kerr, D. D. Meyerhofer, J. Myatt, J. Park, Y. Sentoku, G. J. Williams. Phys. Rev. Lett., 114(2015).
[6] T. P. Yu, A. Pukhov, Z. M. Sheng, F. Liu, G. Shvets. Phys. Rev. Lett., 110(2013).
[7] X. L. Zhu, T. P. Yu, Z. M. Sheng, Y. Yin, I. C. E. Turcu, A. Pukhov. Nat. Commun., 7(2016).
[8] J. Fuchs, T. E. Cowan, P. Audebert, H. Ruhl, L. Gremillet, A. Kemp, M. Allen, A. Blazevic, J.-C. Gauthier, M. Geissel, M. Hegelich, S. Karsch, P. Parks, M. Roth, Y. Sentoku, R. Stephens, E. M. Campbell. Phys. Rev. Lett., 91(2003).
[9] S. Chawla, M. S. Wei, R. Mishra, K. U. Akli, C. D. Chen, H. S. McLean, A. Morace, P. K. Patel, H. Sawada, Y. Sentoku, R. B. Stephens, F. N. Beg. Phys. Rev. Lett., 110(2013).
[10] X. H. Yang, H. Xu, Y. Y. Ma, Z. Y. Ge, H. B. Zhuo, F. Q. Shao. Phys. Plasmas, 25(2018).
[11] M. Borghesi, A. J. Mackinnon, A. R. Bell, G. Malka, C. Vickers, O. Willi, J. R. Davies, A. Pukhov, J. Meyer-ter-Vehn. Phys. Rev. Lett., 83, 4309(1999).
[12] L. Gremillet, F. Amiranoff, S. D. Baton, J.-C. Gauthier, M. Koenig, E. Martinolli, F. Pisani, G. Bonnaud, C. Lebourg, C. Rousseaux, C. Toupin, A. Antonicci, D. Batani, A. Bernardinello, T. Hall, D. Scott, P. Norreys, H. Bandulet, H. Pépin. Phys. Rev. Lett., 83, 5015(1999).
[13] A. J. Kemp, Y. Sentoku, T. Cowan, J. Fuchs, H. Ruhl. Phys. Plasmas, 11, L69(2004).
[14] G. S. Sarkisov, V. V. Ivanov, P. Leblanc, Y. Sentoku, K. Yates, P. Wiewior, O. Chalyy, A. Astanovitskiy, V. Yu. Bychenkov, D. Jobe, R. B. Spielman. Phys. Rev. E, 86(2012).
[15] Y. Bai, Y. Tian, S. Zhou, Y. Zeng, H. Sun, C. Wang, J. Liu. Phys. Plasmas, 24(2017).
[16] A. Debayle, V. T. Tikhonchuk. Phys. Plasmas, 14(2007).
[17] S. I. Krasheninnikov, A. V. Kim, B. K. Frolov, R. Stephens. Phys. Plasmas, 12(2005).
[18] V. T. Tikhonchuk. Phys. Plasmas, 9, 1416(2002).
[19] T. D. Arber, K. Bennett, C. S. Brady, A. Lawrence-Douglas, M. G. Ramsay, N. J. Sircombe, P. Gillies, R. G. Evans, H. Schmitz, A. R. Bell, C. P. Ridgers. Plasma Phys. Control. Fusion, 57(2015).
[20] L. V. Keldysh. Sov. Phys.-JETP, 20, 1307(1965).
[21] M. Ammosov, N. Delone, V. Krainov. Sov. Phys.-JETP, 64, 1191(1986).
[22] N. Delone, V. Krainov. Multiphoton Processes in Atoms, 13(2000).
[23] J. Posthumus, M. Thompson, L. Frasinski, K. Codling. Multiphoton Processes, 298(1997).
[24] A. Haque, M. Alfaz Uddin, A. Basak, K. Karim, B. Saha, F. Malik. Phys. Scr., 74, 377(2006).
[25] M. Guerra, F. Parente, P. Indelicato, J. Santos. Int. J. Mass Spectrom., 313, 1(2012).
[26] O. Klimo, V. T. Tikhonchuk, A. Debayle. Phys. Rev. E, 75(2007).
[27] Y. Hahn. Phys. Lett. A, 23, 82(1997).
[28] Y. Sentoku, A. J. Kemp. J. Comput. Phys., 227, 6846(2008).
[29] Y. Lang, X. H. Yang, H. Xu, Z. Jin, H. B. Zhuo. Plasma Phys. Control. Fusion, 60(2018).
[30] X. H. Yang, M. Borghesi, A. P. L. Robinson. Phys. Plasmas, 19(2012).
[31] H. Xu, X. H. Yang, Z. M. Sheng, P. McKenna, Y. Y. Ma, H. B. Zhuo, Y. Yin, C. Ren, J. Zhang. Nucl. Fusion, 59(2019).
[32] S. C. Wilks, W. L. Kruer, M. Tabak, A. B. Langdon. Phys. Rev. Lett., 69, 1383(1992).
[33] W. Yu, V. Bychenkov, Y. Sentoku, M. Y. Yu, Z. M. Sheng, K. Mima. Phys. Rev. Lett., 85, 570(2000).
[34] V. Yu. Bychenkov, V. N. Novikov, D. Batani, V. T. Tikhonchuk, S. G. Bochkarev. Phys. Plasmas, 11, 3242(2004).
[35] A. Bret. Astrophys. J., 669, 990(2009).
[36] X. H. Yang, X. Xu, H. B. Zhuo, Y. Y. Ma, F. Q. Shao, Y. Yin, M. Borghesi. Eur. Phys. J. D, 68, 30(2014).
[37] X. H. Yang, H. B. Zhuo, Y. Y. Ma, X. Xu, T. P. Yu, D. B. Zou, Z. Y. Ge, B. B. Xu, Q. J. Zhu, F. Q. Shao, M. Borghesi. Plasma Phys. Control. Fusion, 57(2015).
Set citation alerts for the article
Please enter your email address



