- Photonics Research
- Vol. 11, Issue 3, B65 (2023)
Abstract
1. INTRODUCTION
Motivated by their planar architecture and great potential for future on-chip applications, metasurfaces have attracted great attention in recent years [1–9]. In essence, metasurfaces are subwavelength structured thin layers consisting of arrays of scatterers that can be used to control the polarization, phase, and amplitude of light over a subwavelength thickness. In such 2D ultrathin metasurfaces, by spatially varying the geometric parameters of the scatterers, such as shape, size, and orientation, abrupt and controllable changes of optical properties can be achieved via engineering the resonant interaction between light and the scatterers, which offers a fundamentally new method of light manipulation beyond the conventional methods based on refraction or propagation in bulk materials. Metasurfaces not only provide more compact platforms for the study of light–matter interaction in reduced dimensions, but also allow for a plethora of practical applications, such as efficient wavefront shaping, beam steering polarization control, and enhancement of the emission and detection of light.
On the other hand, the concept of topology has also been introduced into the realm of photonics in the past decades, giving birth to the field of topological photonics [10–16]. Topological photonics mainly work according to the bulk-edge correspondence principle, where nontrivial bulk properties of photonic systems manifest through the emergence of topological edge states propagating along the system edges. These edge states are robust against backscattering due to disorder or defects, thus opening a door to design photonic devices with unprecedented performance. While the developments in topological photonics are largely motivated by the relevant topological physics and phenomena discovered in condensed matter physics, which mostly are electronic materials, due to the bosonic nature of photons, topological photonics have their own unique physics and phenomena not present in condensed matter systems.
Topological photonics have been extensively studied in 1D, 2D, and 3D (see Fig. 1 for the schematic). In this review, we will mainly focus on 2D topological photonic systems to illustrate how the research of metasurfaces could be greatly enriched by the integration of optical metasurfaces with topological concepts. We note that though the topological physics and phenomena are much richer in 3D photonic systems, the challenges in fabricating complex nanoscale 3D photonic structures limit their practical compact applications when compared to flat optical components based on metasurfaces, which are much more compatible with the state-of-the-art planar nanofabrication processes, such as integrated photonic circuits. The field of 2D topological metasurfaces (TMs) could be described from the perspectives of passive to active in the classical regime and then to the quantum regime. Here, we remark that traditional metasurfaces refer to the 2D counterparts of conventional metamaterials, which are different from photonic crystals (PhCs) [17]. However, with the rapid progress in the development of metamaterials and metaphotonics, the concept of metasurfaces has already been widely generalized. Currently, the generalized metasurface usually refers to a layer of artificial materials with subwavelength thickness, which can be either structured or unstructured with a series of patterns in horizontal dimensions [18–21].
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
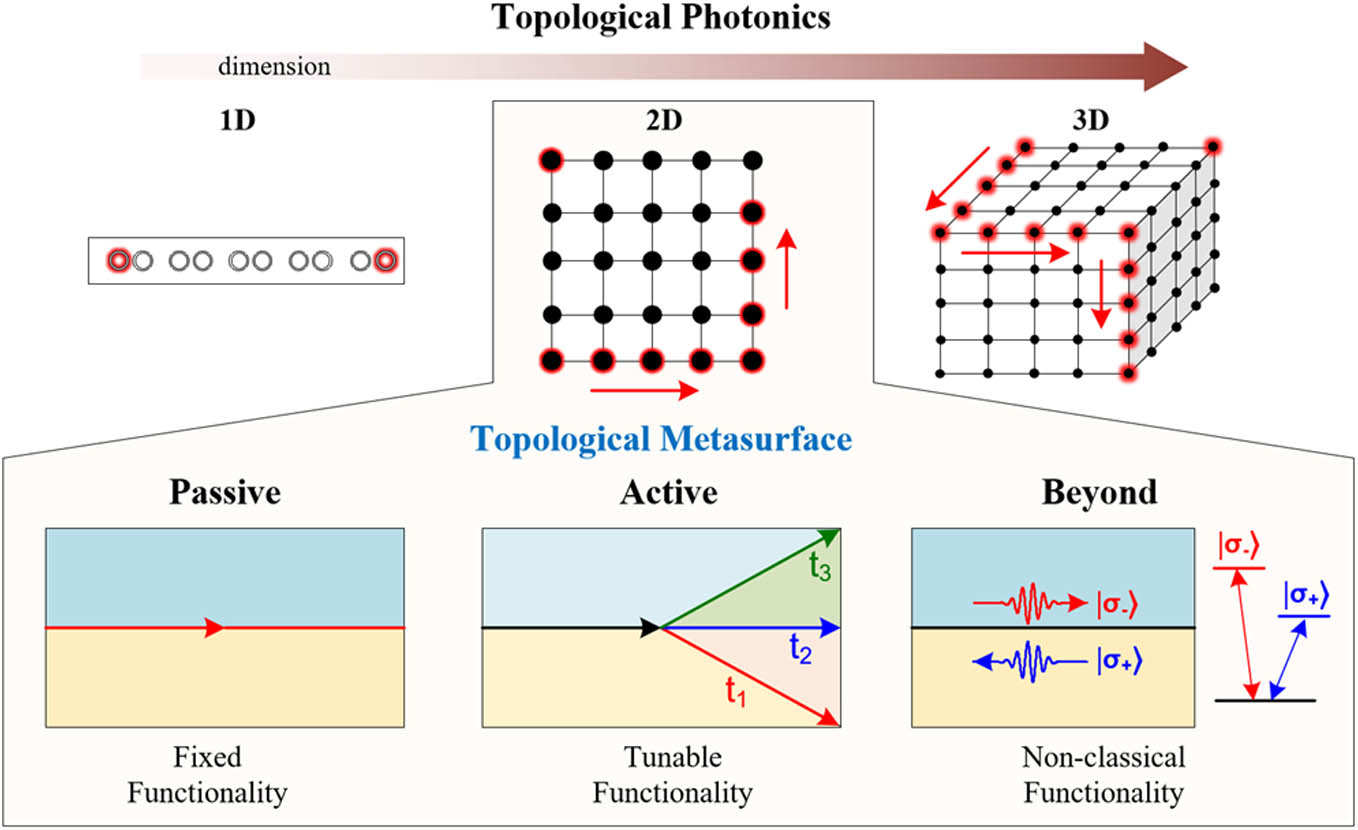
Figure 1.Topological metasurface evolved from passive toward active and beyond.
For passive TMs, which mainly focus on a fixed functionality, we will discuss analog quantum Hall (QH) TM, analog quantum spin Hall (QSH) TM, analog quantum valley-Hall (QVH) TM, Floquet TM, high-order TM, and other TMs, such as bound states in the continuum (BICs) and skyrmions. While passive TMs can provide a static and predefined functionality fixed by the structure of the device, dynamic performance of the metasurface with tunability and reconfigurability or even the integration of multiple optical functionalities into compact metasurface platforms is preferred in most practical applications. We will give an overview on the various methods that have been used in the literature to achieve active control of metasurface properties, such as mechanical, thermal, electrical, or optical methods, and show how the performance of the passive TMs could be dynamically changed. Moving to the quantum regime, we also discuss the non-classical functionalities that TM can perform, such as quantum information applications, where superposition, entanglement, interference, and correlations between multi-photon states of light are crucial. By coupling quantum emitters to TMs, not only high-efficiency quantum photon sources could be obtained, but also via manipulating many-body cooperative interactions among the emitters, strong interacting quantum many-body topological phases of light could be explored.
The review is structured as follows. In Section 2, we discuss passive TMs, including analog QH TM, analog QSH TM, analog QVH TM, Floquet TM, high-order TM, and other TMs, such as BICs and skyrmions. In Section 3, different methods that could be used to actively tune the properties of TMs, such as electrical, optical, mechanical, thermal, and others, are described. In Section 4, TMs for applications ranging from quantum information processes to metasurface–emitter coupling to quantum many-body physics of light are discussed. We conclude in Section 5 and give some future prospects about this fast-evolving field of TMs.
2. PASSIVE TOPOLOGICAL METASURFACE
The TM is a classical-electromagnetics analog counterpart of the 2D electronic topological insulators studied in condensed matter physics. As an important part of topological photonic insulators, TMs can be subdivided into time-reversal (TR)-broken and TR-preserved systems. In this section, we review passive TMs, which mainly focus on a fixed functionality and include analog QH TMs, QSH TMs, QVH TMs, Floquet TMs, high-order TMs, and other TMs.
A. QH Topological Metasurface
An important insight into topology is that topological phases and topological phase transitions are restricted not only to fermions such as electrons in quantum systems, but also to bosons such as photons in classical-wave systems. A prominent example was proposed by Haldane and Raghu in 2008: the robust chiral edge state of electrons in the QH effect (QHE) can also be realized in gyromagnetic PhCs placed in a strong external magnetic field to break the TR symmetry that supports a “one-way waveguide” allowing electromagnetic waves to flow in one direction only [22]. As shown in Fig. 2(a), in a hexagonal 2D array of cylindrical dielectric ferrite rods (such as yttrium iron garnet), when the external magnetic field is zero and TR symmetry is preserved, the hexagonal crystal symmetry guarantees the existence of a pair of Dirac points in the corner of a 2D Brillouin zone (BZ). When placing the gyromagnetic PhCs in a strong external magnetic field to break the TR symmetry, the degeneracy of the Dirac points will be lifted, and each nondegenerate band will exhibit a non-zero Chern number. The nontrivial photonic bandgap will support robust “one-way” photonic chiral edge states that propagate along only one direction and are immune to sharp corners, defects, and disorders. More interestingly, the total number of chiral edge states is exactly equal to the summation of the Chern numbers of photonic bands below the photonic bandgap, which is bulk–boundary correspondence.
![]()
Figure 2.Analog quantum Hall topological metasurface. (a) Bulk dispersion of a gyromagnetic photonic crystal under zero external magnetic field [22]. (b) Experimental setup for measuring the one-way chiral edge state in a gyromagnetic topological metasurface [23]. (c) Gyromagnetic topological metasurface supporting self-guiding unidirectional electromagnetic edge states [24]. (d) Topological bandgap map as a function of magnetic field strength and frequency [25]. (e) Magnetic topological metasurface composed of ferromagnetic rods arranged in a honeycomb lattice [26]. (f) Band structure of magnetic topological metasurface with an unpaired Dirac point [27]. (g) Spectrum and field profiles of the dislocation-induced topological metasurface [28]. (h) Topological phase transition diagram and simulated mode profile of quadrupole topological corner state [29]. (i) Experimental setup for measuring the antichiral edge state [30]. (j) Nonreciprocal large-area topological metasurface [31]. (k) Anomalous nonreciprocal topological metasurface made of ferrite circulators connected with microstrip lines [33].
This pioneering work gave birth to the research area of topological photonics, which have revolutionized the whole field of photonics. In 2009, this fascinating idea was experimentally verified by Wang
Despite the great progress made in 2D photonic Chern insulators, all previous theoretical and experimental studies have been limited to a Chern number of one, which means that photonic Chern insulators support only one chiral edge state according to bulk–boundary correspondence. It is highly desirable to construct photonic Chern insulators with large Chern numbers and multiple chiral edge states. By simultaneously gapping multiple sets of Dirac and quadratic degeneracies, Skirlo
Besides the robust chiral topological edge states, another type of fundamental component in photonic chips, robust topological cavity modes, can also be realized in a gyromagnetic PhC. Li
From the celebrated Haldane model that exhibits the QHE with broken TR symmetry, two chiral edge states will propagate in opposite directions along two parallel edges of a magnetic PhC stripe sample. However, in a modified Haldane model, a counterintuitive physical phenomenon is experimentally observed in which two antichiral edge states can propagate in the same direction along two parallel strip edges [30]. The underlying physical mechanism of antichiral edge states can be described by a modified Haldane model, where the next-nearest-neighbor couplings for different sublattices have opposite signs in phase. The experimental sample shown in the top panel of Fig. 2(i) is a honeycomb magnetic PhC with two sets of sublattices magnetically biased in opposite directions. The measured antichiral edge states will propagate in the right direction along both upper and lower stripe edges, as shown in the bottom panel of Fig. 2(i). While the previously mentioned chiral or antichiral edge states propagate along a certain narrow edge, Wang
Though photonic Chern insulators are regarded as the most robust topological phases reported so far, recently, Zhang
B. QSH Topological Metasurface
The concept of the QSH effect (QSHE) was first proposed in condensed matters [34] and observed in semiconductors [35,36], which can be regarded as two copies of QH states, where electrons feel spin-dependent magnetic fields. In a QSH system, TR symmetry is preserved, which releases the requirement of strong magnetic fields in QH systems. Due to the spin-1/2 of electrons, TR symmetry guarantees the Kramers doublet of electronic states composed of spin-up and spin-down states at TR-invariant points. When the spin-orbit coupling (SOC) is considered in the QSH system, spin-dependent gauge fields are introduced to unfold the Kramers double degeneracy of electronic states away from TR points, while the degeneracy at TR-invariant points is still degenerate. For a finite-sized system composed of two regions with different topological invariants, two topological edge states with opposite spins and momenta can be supported, each of which is spin-momentum locked, backscattering immune, and robust against perturbations that avoid spin flipping.
When it comes to the classical counterpart of QSHE, the TR symmetries for both photons and phonons are bosonic with , where Kramers degeneracy is not guaranteed. To emulate the QSHE for a photonic system, an essential step is to construct Kramers degeneracy by pseudospin states with pseudo-TR symmetry satisfying . The first proposal for photonic QSHE was developed by Khanikaev
![]()
Figure 3.Photonic analogs of the quantum spin Hall effect. (a) Band structure of a metacrystal with a hexagonal lattice [37]. (b) Experimental realization of QSHE by metacrystal waveguides [38]. (c), (d) Theoretical proposal [39] and experimental realization [40] of QSHE by bi-anisotropic metawaveguides. (e) Schematic of a triangular all-dielectric photonic crystal as a photonic analog of QSHE [42]. (f)–(j) Experimental realization of QSHE by crystalline metamaterials in the microwave range (f) [43], (g) [44], visible spectral range (h) [45], near-infrared region (i) [46], and terahertz range (j) [47].
Another method to realize the photonic analog of QSHE was theoretically proposed by Ma
On the other hand, another paradigm to implement photonic analogs of QSHE via crystalline symmetries was proposed by Wu and Hu [42]. Dirac cones merge at BZ corner K and points when solving the band structure of a rhombic primitive unit cell. When considering an enlarged unit cell consisting of six dielectric cylinders [Fig. 3(e)], the Dirac cones fold back to the point, which induces a double Dirac cone at the center of the first BZ comprising two dipole modes and two quadrupole modes. To emulate the QSHE, pseudospins are constructed by dipole modes and quadrupole modes, while SOC is realized by shrinking or expanding the distance of cylinders, which induces a topological phase transition from POIs to PTIs. Topological edge states with a spin-momentum locking property can be realized at the interface between POI and PTI.
The realizations of photonic analogs of QSHE by crystalline symmetries require simple and practicable configurations in experiments, which promotes the extension to other frequency regimes and platforms [43–47], such as the experimental realization of QSHE by subwavelength resonant metal antennas [Fig. 3(f)] and all-dielectric PhCs [Fig. 3(g)] at the microwave regime. Later, the topological edge states for the QSH system were experimentally realized by a honeycomb lattice composed of nanoscale silicon Mie resonators in the visible spectral range [see Fig. 3(h)]. Robust transmission of topological edge states in the photonic analog of QSHE was experimentally verified with a single quantum emitter and a 2D PhC slab in the near-infrared region, where strong light–matter coupling in the quantum domain was explored [Fig. 3(i)]. Subsequently, the spin-momentum locking and chiral routing along with sharp corners of topological edge states were experimentally demonstrated in a silicon photonic platform at telecom wavelengths by far-field radiation [Fig. 3(j)].
C. QVH Topological Metasurface
Inspired by the research advances in 2D materials, especially [48] and graphene [49,50], the topological valley-Hall insulating phase has been introduced into photonics [51–84]. The valley refers to the local extremum of the conduction band or the valence band, usually appearing at the corners of the BZ. The excited states at each valley carry opposite angular momenta, providing valley-locked orbital magnetic moments, which are also known as valley pseudospins. Over the past few years, much attention has been given to metasurfaces with the topological valley-Hall insulating phase (topological valley-Hall metasurfaces, for short) [58,64,65,67–69,71–74,76,78,79,84,85], which exhibit many intriguing phenomena attached to valley-contrasting physics, such as the photonic valley-Hall effect, valley-locked bulk transport, and valley kink states. Exploiting the topological valley-Hall insulating phase has enabled many promising applications in robust waveguides [69,85], on-chip communications [86], and antennas [54]. In this section, we will introduce the fundamental physics and potential applications of topological valley-Hall metasurfaces.
Different from photonic Chern insulators with broken TR symmetry [23,87,88] and spin-Hall PTIs protected by TR symmetry [42,44,89], valley-Hall PTIs require the breaking of inversion symmetry () [53]. Considering a graphene-like PhC featuring two Dirac cones, when perturbatively breaking , the pair of Dirac cones will be lifted, and a bandgap opens at valley. The band structure around valley can be described by a massive Dirac equation, with a mass term , whose magnitude measures the bandwidth and sign is determined by the non-zero local Berry flux at the valley [see Fig. 4(a)]. In addition, the topological property comes from the non-zero local Berry curvatures, defined by
![]()
Figure 4.Valley-Hall PTI and its metasurface realizations. (a) Illustration of Dirac cones with different mass terms located at the corners of the Brillouin zone. (b) Schematic diagram of domain wall consisting of two valley-Hall PTIs. (c) Dispersions of the supercell shown in (b) (dashed rectangle). (d) Typical unit cells of topological valley-Hall metasurfaces. (e) Statistics of existing literature on topological valley photonics by June 2022. Each bubble denotes a theoretical/experimental (hollow/solid) literature on active/passive (red/blue) devices. The size denotes the number of citations.
A remarkable property of the valley-Hall PTI is that at the interface consisting of two valley-Hall PTIs with opposite valley-Chern numbers, dubbed the domain wall [see Fig. 4(b)] [49], a pair of gapless boundary modes (also known as valley kink states) appears. Due to the preserved symmetry, the valley kink states bounded to different valleys have opposite group/phase velocities, as shown in Fig. 4(c). Owing to their valley-locked chirality [53], the valley kink states can scatter only to themselves and transfer the energy among the same valleys in the BZ, even if the domain wall is bent by 120°. Hence, the valley kink states can go nowhere but pass through the sharp corners, implying its robustness to certain types of disorders. To date, different kinds of unit cells with broken have been designed to realize valley-Hall PTIs. This can usually be achieved by lowering the lattice symmetry from or to , in a triangular or honeycomb lattice, as shown in Fig. 4(d).
The study of topological valley-Hall metasurfaces is not only a scientific curiosity but has also led to many promising applications. Having introduced the fundamental physics of the topological valley insulating phase, herein, we will focus on the development of topological valley-Hall metasurfaces from the perspective of practical applications. In general, photonic devices can be classified as passive and active based on whether additional pump sources or active control is required. In Fig. 4(e), we present the statistics of existing literature on topological valley photonics as of June 2022. As one can see, there are two tendencies in the recent five years: (i) from microwave to optics; (ii) from passive to active. In this subsection, before proceeding to the active devices based on valley-Hall PTIs that involve gain or dynamic control, we will first review the passive devices.
High-speed on-chip communications are of the essence in modern information and communication technologies, including optical integrated circuitry and on-chip interconnects, which require high-efficiency, low-loss, integrated, and robust solutions to waveguiding. Compared to conventional PhC waveguides or other nontopological optical waveguides, topological valley kink states hold great potential for on-chip communications, owing to their intrinsic properties, including topological robustness against defects (determined by the band topology), single-mode propagation (guaranteed by the valley-Chern number difference at domain walls), and linear dispersion (governed by the low-energy Dirac equation). Applying the valley kink states to on-chip communications has been experimentally demonstrated at terahertz (THz) frequencies recently [86]. As shown in Fig. 5(a), the designed THz on-chip valley-Hall PTI has a graphene-like lattice, where an array of triangular holes is patterned on a high-resistivity suspended silicon metasurface with low absorptive losses. As expected, the valley kink states supported by the silicon metasurface are topologically robust and can pass through multiple sharp bends (five 120° bends and five 60° bends) with almost unity transmission. Moreover, an error-free transmission with a data transfer rate up to 11 Gbit/s around 0.33 THz was also demonstrated experimentally, which further enables real-time transmission of uncompressed 4K high-definition video. The robust on-chip propagation of valley kink states has also been demonstrated at optical frequencies [67,69], and the corresponding on-chip optical communications require further experimental exploration.
![]()
Figure 5.Passive photonic devices based on topological valley-Hall metasurfaces. (a) Silicon topological valley-Hall metasurface for on-chip THz communication [86]. (b) Simulated field distribution for structure in (a) [86]. (c) Measured bit error rate as a function of data rate at 0.335 THz [86]. (d) Momentum-space analysis on the outcoupling of (e) simulated (left) and measured (right) field patterns for the outcoupling of TE-mode valley kink state to vacuum space [54]. (f) Measured reflectance for zigzag (gray) and armchair (purple) terminations [54]. (g) Schematic diagram of photonic routing based on the valley kink states [67]. (h) Scanning-electron-microscope (SEM) view of the experimental sample [67]. (i), (j) Measurement of photonic routing profiles at
Apart from the on-chip communication, valley kink states can also offer the possibility for high-efficiency coupling to the surrounding environment with a certain type of termination, which can be used to devise reflectionless directional antennas [51,54,72]. Figures 5(d)–5(f) show the experimental demonstration of topological refraction of valley kink states to ambient space [54]. In experiments, a phased array of dipole antennas was placed at the center of the domain wall [white rectangle in Fig. 5(e)] to selectively excite rightward valley kink states. The excited kink states then outcouple to the ambient space through a valley-preserving zigzag termination with negligible reflection that usually requires joudicious design of impedances in the conventional outcoupler [see Fig. 5(e) and the purple curve in Fig. 5(f)]. The refraction direction can be understood according to the momentum phase-matching conditions at the terminal interface [see Fig. 5(d)]. In contrast, as the valley conservation is broken at the armchair termination, the photonic energy is inevitably coupled to the backward channel, resulting in strong reflection [gray curve in Fig. 5(f)]. The high-efficiency outcoupling from valley kink states to ambient space may find potential applications such as directional antennas, lasers, and wireless communications.
Owing to the property of valley-locked chirality, valley kink states can be used to devise all-optical routers operational at telecommunication wavelengths, which was realized recently [67]. The experiments were performed in a silicon-on-insulator (SOI) platform, as shown in Figs. 5(g) and 5(h). The photonic router consists of two valley domain walls connected with two nonuniform grating couplers and a microdisk connected with two 373-nm-wide strip silicon waveguides [labeled WVG1 and WVG2 in Fig. 5(g)]. The close-to-diffraction-limited microdisk serving as a phase vortex generator transforms the waveguide mode from WVG1/WVG2 input waveguides to a clockwise/counterclockwise vortex field. Owing to valley-chirality locking, the vortices with opposite chiralities are converted to different valley kink states with opposite valleys, and then couple to free space via grating couplers. Valley-chirality locking also enables topological channel intersection [72], where the valley transport path depends solely on the geometries of the intersection.
D. Floquet Topological Metasurface
Floquet topological insulators (FTIs) [91,92], a class of time-varied systems hosting robust edge states against disorders, have attracted intense research interest across many disciplines from condensed matter physics to photonics. The dynamics of FTIs are governed by evolution equations , where is the evolution operator, and is the wave function. Basically, revealing the evolutions is foremost in understanding periodic modulations , where is the temporal period of the modulation, and represents the effective Floquet Hamiltonian [93]. Unlike band diagrams of static Hamiltonian systems bounded by ground states, exhibits periodic quasi-energy band diagrams , with corresponding eigenstates satisfying . Generally, can be written as , where and the unit matrix form an orthogonal basis for matrices in Hilbert space. The bulk topologies of FTI are characterized with a Chern number, , where . Intuitively, fruitful Floquet topological phases can be anticipated from distinct modulations, which is challenging to realize in condensed matter systems [94,95]. Due to the easy implementations and flexibilities in wave manipulations, photonic metasurfaces hold promise in demonstrating FTI phases. On the other hand, exotic FTI phases offer novel approaches to manipulate light, thus promising unusual photonic applications.
Theoretically, fruitful Floquet topological phases have been predicted on various time-variant photonic systems [96–133], including Floquet Chern topological insulators (FCTIs) [96–100] and anomalous FTIs (AFTIs) [100]. Regarding FCTIs, whose bulk bands are characterized by non-zero Chern numbers, two types of models (i.e., discrete and continuum) have been proposed. In 2012, a square lattice of photonic resonators with a synthesized Landau gauge was proposed to break TR symmetry by Fang
![]()
Figure 6.(a) Dynamically modulated photonic resonator lattice exhibiting an effective magnetic field for photons [96]. (b) Kagomé lattice with three sites in the primitive cell, and the corresponding Brillouin zone [97]. (c) The FTI consists of a static PhC and permittivity modulations by three Bloch waves [98]. (d) Non-Hermitian Floquet kagomé lattice [100].
In AFTIs, robust chiral edge states appear even though the Chern numbers of all the bulk Floquet bands are zero, and the topological invariants characterizing AFTIs are winding numbers. Li
Because temporal modulation itself in either optical or mechanical systems is a rather challenging task, many proposals remain theoretical. By contrast, effective modulation [102–107] creates the possibility of a practical implementation of FTIs. Currently, effective modulations are all based on coupled ring resonator systems. The method of effective modulation was theoretically proposed by Liang
![]()
Figure 7.(a) Schematic of a unit cell in a 2D lattice of photonic ring resonators (upper) and the equivalent periodic network (lower) [103]. (b) Photo of metallic rods on a flat metallic surface (left), and schematic of a
The AFTI phase based on the network model was first demonstrated by Gao
The first experimental realization of an FTI on a nanophotonics platform was reported [106] in 2020. As shown in Fig. 7(d), their sample is a square lattice of strongly coupled octagonal resonators in the SOI material system, and resonators A and D have different coupling coefficients with their respective adjacent resonators. As light circulates around each microring, it interacts periodically with its neighbors with different coupling coefficients; the lattice is thus equivalent to a periodically driven Floquet system. By exploiting the frequency dispersion of the evanescent couplers to adjust the coupling strength, they experimentally demonstrated the topological phase transition between FCTI and AFTI. The realization of on-chip FTI has also spawned applications.
To date, FTIs based on dynamic modulations have not been experimentally demonstrated, due to the extremely weak electro-optical effects and nonlinearity of materials, especially at high frequencies. On the other hand, effective modulations have been experimentally demonstrated; however, they are so far limited in a coupled ring resonator scheme. Straightforwardly, more effort would be needed on advanced experimental technologies for dynamically modulated FTI and effective modulation schemes beyond coupled ring resonators arrays. More intriguing physics could be anticipated by connecting the FTI with other mechanisms, i.e., non-Hermicity [108,109] and quantum optics [110,111].
E. High-Order Topological Metasurfaces
Different from conventional topological states where the topological boundary states appear at one dimension less than bulk, second corner states are higher-order topological phenomena where the topological boundary states appear in dimensions at least second-order lower than bulk [112,113]. This new topological phase has been explored in different photonic structures and has found diverse applications, which we will discuss in this section.
The most popular models on topological corner states in photonic systems are based on the 2D Su–Schrieffer–Heeger (SSH) model, in which each unit cell contains some cylinders, and by expanding or shrinking the cylinders’ positions away from or towards the center of the unit cell, intra-cell and inter-cell hopping can be tuned, leading to a topologically trivial to nontrivial transition. For the square lattice 2D SSH model [114], as shown in Fig. 8(a), it considered a 2D PhC with four identical dielectric rods in each unit cell, and by adjusting the distances between the nearby rods in and directions, the emergence of edge and corner states can be controlled straightforwardly. The 2D square SSH model was experimentally realized in PhC slabs with periodic dielectric rods on a perfect electric conductor [115] and in PhCs consisting of alumina cylinders sandwiched between two metallic plates [116]. Moreover, based on the coupled dipole approximation, the polarization-dependent topological phase of an array of metallic nanoparticles in a 2D SSH lattice has been studied [117], showing that polarization can serve as a new degree of freedom to control the topological features and develop robust multifunctional photonic devices.
![]()
Figure 8.Second-order photonic corner states. (a) Second-order photonic corner states in a photonic crystal with dielectric rods [114]. (b) Second-order photonic corner states in a kagomé metasurface [119]. (c) Photonic crystal nanocavity based on a topological corner state [120]. (d) Enhanced photoluminescence mediated by a topological metasurface [122]. (e) Quadrupole topological phase in a twisted photonic crystal [129].
Corner states have also been studied in a kagomé lattice whose unit cell contains three cylinders. Especially, corner states in kagomé lattices have been experimentally observed in arrays of dielectric cylinders arranged to form a kagomé lattice between two parallel aluminium plates [118], and in metasurfaces fabricated on an SOI chip consisting of trimers of diamond-shaped holes [119], as demonstrated in Fig. 8(b). Interestingly, in addition to corner states due to nearest-neighbor interactions, a new class of topological corner states induced by long-range interactions with a purely electromagnetic nature, which has no analogy in condensed matter systems, exists in the kagomé structure.
Corner states can serve as high-Q cavity modes, thus providing potential applications in enhancing light–matter interaction. As shown in Fig. 8(c), a corner state tightly localized in space with a high Q factor over 2000 was experimentally observed in Ref. [120], verifying its promise as a nanocavity. Corner states could be pumped using in-plane excitation conditions as experimentally demonstrated in Ref. [121] and could be used for enhancement of a photoluminescence (PL) signal [122] [depicted in Fig. 8(d)], and rainbow trapping [123]. For example, multiband corner states have been designed via the topological optimization method [124], in which the system supports four highly localized corner states within four sizeable bandgaps that are robust to bulk impurities. The recently proposed dual-polarization topological corner states for both transverse electric and transverse magnetic modes [125] and a new principle for creating corner states within odd-order bandgaps in -symmetric lattices beyond the 2D SSH paradigm [126] open new possibilities for both fundamental science and promising applications.
While corner states could emerge due to a nontrivial bulk dipole moment as discussed above, they can also appear due to a nontrivial bulk quadrupole moment without a dipole moment. This kind of insulator is called a quadrupole insulator in the literature and is challenging to implement using photonic systems due to the existence of negative couplings in the original pi-flux model. To date, there are only a few works investigating quadrupole topological states in photonic systems [29,127–129]. In Ref. [127], the authors experientially implemented negative coupling in a 2D lattice of nanophotonic silicon ring resonators and demonstrated that quantization of the bulk quadrupole moment manifests as topologically robust 0D corner states. Negative coupling could also be introduced in a lattice of plasmon-polaritonic nanocavities exploiting the geometry-dependent sign reversal of the couplings between daisylike nanocavities [128] or in gyromagnetic PhC through a double-band-inversion process [29]. More interestingly, quadrupole topological phases could be realized in all-dielectric PhCs without the pi-flux-threading mechanism as experimentally demonstrated in PhCs composed of dielectric cylinders via twisting the unit cell [129], as shown in Fig. 8(e).
The dispersive topological edge states for QSHE in PTI can be used to realize topologically protected mid-gap defect modes (or corner modes) by opening a bandgap for the edge state. Topological corner modes with small mode volumes are robust against structure deformations, which was first observed by Noh
Based on Floquet HOTIs, topological states with dimensions two or more lower than that of bulk can also be studied in Floquet TMs. Connecting with the concept of synthetic dimensions, Dutt
F. Other Topological Metasurfaces
1. BICs
BICs can completely confine light by eliminating radiation loss even though their frequencies and momentum are embedded in the continuum spectrum [134]. BICs were first mathematically proposed in 1929 by von Neumann and Wigner in quantum mechanics with artificial quantum potential [135]. BICs were subsequently realized as destructive interference [136] and attracted broad attention in both quantum and classical waves. They can be roughly classified as symmetry-protected BICs and off-Γ BICs. Symmetry-protected BICs [137–139] are realized when there is a symmetry mismatch between resonances and radiation channels. Off-Γ BICs can be realized by various mechanisms. For example, Friedrich–Wintgen BICs (FW-BICs) are generated when there is destructive interference among multiple resonances [136,140,141]. Tunable BICs can be realized when there is an accidental cancelation of radiation loss at one single band [142]. Radiation channels can be reduced by environmental design to achieve BICs [143]. BICs with an infinite lifetime can improve light confinement and have shown benefits in boosting light–matter interactions.
BICs have been recently revealed as topologically protected polarization singularity in momentum space [144]. Polarizations of far-field radiation evolve and form vortices around a BIC, as shown in Fig. 9(a). The winding number of polarization defines the topological charge of a BIC. BICs with undefined polarization have vanishing coupling with radiation channels and therefore are confined with an infinite Q factor. The topological nature was theoretically proposed by Zhen
![]()
Figure 9.(a) Far-field polarizations form vortices with BICs as polarization singularities [144]. (b) Multiple BICs are tuned together as a merging BIC. The
When multiple BICs are tuned to the same point, a merging BIC is created, which is promising in designing a super-high-Q cavity. Although BICs have infinite Q factors theoretically, there are inevitable fabrication imperfections that can couple BICs with nearby radiative states through scattering, which limits the available Q factor. To further improve light confinement, Q factors of nearby radiative states need to be enhanced. As for an isolated BIC, the scaling rule of Q factors decaying away from the singularity has been limited by its topological charge. Recently, merging BICs have been proposed by Jin
When BICs are broken by reducing symmetry, the topological charge cannot disappear and will split as smaller topological charges following topological charge conservation. Liu
BICs with infinite Q factors are promising in boosting the performance of light propagation [154–159]. Zero-index materials have been designed in all-dielectric PhCs with Dirac cone dispersion to alleviate ohmic losses. However, they suffer from out-of-plane radiation loss that hinders their development. BICs have been introduced to completely eliminate radiation loss. As theoretically demonstrated by Minkov
![]()
Figure 10.(a) Zero-index materials with light confined by BICs in out-of-plane [156]. (b) Diffraction-free beams are guided by BICs beyond the light cone [159]. (c) Ultrasensitive hyperspectral imaging by detecting BIC-inspired resonance shifts [162]. (d) Angular-scanning sensors using BIC-inspired narrow spectra [163]. (e) Optical vortices generated from the polarization vortex around BICs [166].
Metasurfaces supporting BICs possess ultrasharp resonances and strong light confinement, which can be extremely sensitive to refractive index changes [160–165]. Chemical or biological sensing enhanced by BICs has been explored recently. Yesilkoy
The topological property of polarization winding around BICs provides a feasible approach for generating optical vortices. As demonstrated by Wang
2. Skyrmions
Skyrmions are topologically stable quasiparticle excitations initially proposed as a nucleon model in 1961 [167–169]. Skyrmions have been predicted and investigated in liquid crystals (LCs) [170] and Bose–Einstein condensates [171], and are most commonly known in thin-film magnetic materials [172–177] due to their promising potential in spintronics. Recently, skyrmions and related concepts have also drawn much attention in electromagnetic waves. Here, as before, we restrict our review to 2D systems and briefly introduce the recent advances of skyrmion-related concepts in light.
Skyrmion-related objects define topological nontrivial three-component vector fields (denoted by ) over a 2D coordinate space . The skyrmion number can characterize the topology of this nontrivial vector field distribution [178,179]:
In typical situations, the magnitude of is irrelevant, and thus forms a two-sphere . Skyrmions as quasiparticle excitations are assumed to be embedded in a uniform background, and thus at the outskirt of skyrmions is the same. One can merge the edge of the skyrmion into a single point, and then the 2D coordinate space also forms a two-sphere . The skyrmion number defines a map characterized by the second homotopy group of the sphere . Here, the skyrmion number gives the topologically distinct ways that the unit vector field wraps around the sphere formed by the coordinate space.
A skyrmion number alone is not enough to uniquely determine the spin texture. Figures 11(a) and 11(b) show the vector field of Bloch-type [180] and the Néel-type [181] skyrmions with , respectively. To characterize the difference between different types of skyrmions, one can write the unit vector field as , where , and is the polar angle of the 2D coordinate space. Then,
![]()
Figure 11.(a) Bloch-type skyrmion and (b) Néel-type skyrmion with
There are many generalized forms of quasiparticles that enrich the skyrmion family [182–184]. For example, two skyrmions with opposite polarities can form a skyrmionium with zero skyrmion number while still having a nontrivial local spin texture distribution. Another important family generalization of topological quasiparticles is meron and antimeron, with topological charges and , respectively. Meron (antimeron) might present in thin-film magnetic materials when the material’s response is largest under an in-plane external magnetic field. The relation between a skyrmion and a meron (antimeron) is illustrated in Fig. 11(c). The unit vector at the center points up or down, and those at the periphery align in the plane, exhibiting nontrivial windings. Generalizations of merons (antimerons) such as those with higher topological charges or combinations of two with opposite charges (similar to skyrmionium) can be constructed following similar rules.
Here, our review is restricted to 2D systems, and thus other skyrmion-related concepts such as flying skyrmions or optical hopfions are not introduced. Since skyrmion-related concepts try to build maps between a unit vector field and a 2D coordinate space, a simple way of classifying them is through how we construct and the 2D coordinate space. Electromagnetic waves are three-component complex vectors. There are, in general, three approaches to defining a unit vector field with electromagnetic waves. The first approach is to construct standing waves and then use the resulting real electric or magnetic fields as vector fields (also dubbed as field skyrmions). The second one is to use the spin vectors of evanescent electromagnetic fields [185–192]. The third approach uses the fact that the polarization of light in free space maps onto the Poincaré sphere. Thus the polarization distribution forms a unit vector field with the vector pointing from the origin to the corresponding locations on the Poincaré sphere. For 2D coordinate systems, two natural choices are real space and momentum space.
We start with optical field skyrmions wherein the electric (magnetic) field plays the role of the vector field . SP polaritons (SPPs) on 2D surfaces are good candidates for studying the optical analog of skyrmions. Indeed, an optical field skyrmion lattice was first observed within SPPs [193].
The spin vector of evanescent electromagnetic fields () can also be chosen as the vector field. The spin vector of light is defined as , where and are the electric and magnetic fields, is the frequency, and and are the permittivity and permeability, respectively. By tightly focusing a vortex beam (with non-zero orbital angular momentum), the longitudinal component (parallel to the propagating direction) of the spin vector can be introduced, and a skyrmion-like texture is formed in the focal plane near the beam axis [194]. Here, the boundary of skyrmion-like texture is not well defined. Spin-skyrmion lattices and spin-meron lattices can also be constructed through spin–orbital coupling in vortex beams by adequately choosing the symmetry of optical fields [195–200].
Besides the electric field and spin of evanescent electromagnetic fields, the polarization of light is another choice for the unit vector field . Spatial polarization distribution, say in a vector beam, can simulate optical skyrmions [201]. Such a kind of vector beam has been proposed before in the name of full Poincaré beams, and its relation to skyrmion physics has been revealed only recently [202]. Different types of skyrmions, i.e., different polarization distributions of beams, can be generated passively with a spatial light modulator [203] or actively with a proper angular grated laser [202]. Going one step further, the unit vector field can also be the pseudospin of a two-level system. Such a scheme has been used to construct pseudospin skyrmions in nonlinear media [197].
The optical skyrmions discussed above are mostly defined in real space. The momentum space (reciprocal space) of a 2D system can also play the role of a coordinate system. The spin texture of electronic systems in momentum space has already been investigated in topological insulators [204,205]. In photonics, one can project eigenmodes onto freely propagating waves, which then define the polarization of eigenmodes. The variation of eigenmode polarizations is related to the Berry phase in momentum space. A 2D PhC slab with a hexagonal lattice is known to process a Dirac cone at the K point and point in reciprocal space. Slightly breaking the inversion symmetry induces a Berry phase localized around the valley, and this Berry phase further causes a meron (antimeron) of polarization distribution [206]. Such a PhC slab can also be used to generate light bullets carrying meron spin texture [207].
3. ACTIVE TOPOLOGICAL METASURFACE
Due to exotic functionalities including unidirectional light propagation and immunity to disorder or defect, TMs have attracted extensive attention in both fundamental research and practical applications. However, most current TMs are passive, and primarily focus on the development of static photonic systems to realize a specific photonic topological phenomenon or functionality, and hence their nonlinearity and reconfigurability are limited. In this section, we review the cutting-edge studies on active TMs, which are split into two parts: nonlinear TMs and reconfigurable TMs.
A. Nonlinear Topological Metasurface
Recent works have shown that combining TM and nonlinear optics can produce a variety of promising applications and important phenomena, including topologically protected frequency converters, high-resolution sensors, topological solitons and modulators, topological lasers, as well as nonlinearity-induced topological phase transitions. These developments not only demonstrate that the active TM can result in some emerging phenomena and functionalities not presented in passive regimes, but also suggest that nonlinearity can offer promising applications for novel active devices. As listed in Table 1, we review some typical nonlinear effects and the corresponding applications exhibited in nonlinear TMs, including frequency conversion, parametric amplification, Kerr effect, etc. Typical Nonlinear Effects in Active Topological Metasurface Quantum source (QS); photon entanglement (PE); harmonic generation (HG); frequency converter (FC); frequency comb (FCB); lithium niobate (LN or Effect Platform Application Medium Frequency Results Refs. SHG HOTI FC Dielectric Sim [ BIC FC GaSe Exp [ QVH Sensing Dielectric Sim [ HOTI FC Te 28.4 THz Sim [ QSH FC AlGaAs Sim [ BIC FC Exp [ BIC FC Si Exp [ THG QSH Imaging Si Exp [ BIC FC Si Exp [ QH FC Dielectric Sim [ HOTI Imaging Si/Al Exp [ FWM QH QS Si Exp [ QH Amplifier Graphene Sim [ QH FCB Si Sim [ QVH PE Si Sim [ Floquet Emitter Si Exp [ HHG BIC FC Si Exp [ BIC OAM Si Sim [ Kerr Floquet Modulator Silica Exp [ Floquet Soliton Exp [ HOTI Soliton Silica Exp [ QSVH Modulator Sim [ Other QH Laser InGaAsP/YIG Exp [ BIC Laser InGaAsP Exp [ BIC Laser GaAs Exp [ QH Laser InGaAsP Exp [ QVH Laser InGaAsP Sim [ QVH Laser Exp [ HOTI Laser InGaAs Exp [ BIC Laser 543 THz (0.552 Exp [ QSH Laser InGaAsP Exp [ QSH Laser Exp [ BIC Laser Exp [
1. Frequency Conversion
Frequency conversion is a nonlinear optical process where light interacts with a nonlinear material leading to generation of new photons with different frequencies. Generally, typical nonlinear effects in frequency conversion include second-harmonic generation (SHG), third-harmonic generation (THG), four-wave mixing (FWM), high-harmonic generation (HHG), Kerr effect, etc. Since the intrinsic nonlinear susceptibility of most natural materials is very weak, it is a critical mission to find a powerful approach to enhance nonlinear frequency conversion. The field distribution in TM can be remarkably enhanced in the system edge or corner; thus the active TM is a promising platform to implement highly efficient frequency conversion and explore novel functionalities.
SHG, also well known as frequency doubling, is generally characterized by the second-order nonlinear susceptibility of a nonlinear material, where two photons with the same frequency are absorbed to generate a new photon with twice the frequency of the pump photons. Recently, a high-order TM to use second-order topological corner modes for more efficient SHG and control has been explored [208]. As shown in Fig. 12(a), two topological bandgaps of a dielectric PhC are optimized to support corner states that could be frequency matched to realize high-efficiency SHG through the mechanism of double resonance.
![]()
Figure 12.Second-harmonic generation (SHG) in active topological metasurface. (a) SHG mediated by two corner modes that reside within two different topological bandgaps and could be frequency matched to greatly boost harmonic conversion efficiency by the mechanism of double resonance [208]. (b) Spatial mapping of SHG in a fabricated slotted nanocube array [214]. (c) Band diagram and simulated field intensities of fundamental (
High-Q resonances based on BICs have shown tremendous improvement in nonlinear conversion efficiency [140,245–252]. In a subwavelength dielectric nanoparticle, two coupled resonances can evolve into a quasi-BIC. The high-Q mode has theoretically predicted and experimentally demonstrated that nonlinear conversion efficiency in harmonic generation can be enhanced by more than two orders of magnitude [140,247,248]. The design of nonlinear metasurfaces has been inspired to achieve giant nonlinear effects through BICs. Liu
Based on the analog QVH effect, the TM is also a good platform to explore novel phenomena in SHG. For example, an all-dielectric TM, which has double topological valley-Hall kink modes, was proposed recently [210]. By gapping out the corresponding Dirac points, two topological frequency bandgaps can be created around a pair of frequencies, namely, fundamental and second-harmonic frequencies. The corresponding numerical results prove that valley-Hall kink modes along a kink-type domain wall interface can be generated within the two frequency bandgaps, where tunable, bidirectional phase-matched SHG via nonlinear interaction of valley-Hall kink modes can be achieved, as demonstrated by the SHG field distributions in Fig. 12(c).
THG, also called frequency tripling, is generally characterized by the third-order nonlinear susceptibility of a nonlinear material, where three photons with the same frequency are absorbed to generate a new photon with thrice the frequency of pump photons. As depicted in Fig. 13(a), based on the higher-order topological effect, a silicon TM, which can support topologically protected helical edge states, has been experimentally studied [215] recently. Due to enhancement boosted by multipolar Mie resonances of silicon nanoparticles, a strong THG is measured. Moreover, the independent high-contrast imaging of either bulk modes or spin-momentum-locked edge states was explored under different pump-beam wavelengths. They also demonstrate the pseudospin-dependent unidirectional waveguiding of edge states bypassing sharp corners.
![]()
Figure 13.Third-harmonic generation (THG) in active topological metasurfaces. (a) THG in a QSH topological metasurface consisting of silicon pillars arranged into hexagon clusters [215]. (b) THG in a nonlinear and asymmetric metasurface governed by BIC [216]. (c) THG enhanced by a topologically protected edge mode in high-order topological metasurfaces [218].
In addition to the QSHE, based on BICs, a silicon-based metasurface composed of meta-atoms with broken in-plane symmetry has been designed to tailor THG efficiency by engineering the degree of unit cell asymmetry [216], as shown in Fig. 13(b). Furthermore, the effect of radiative and nonradiative losses on nonlinear conversion efficiency is discussed based on the concept of the critical coupling of light to metasurface resonances. By tuning the metasurface parameters to the regime of critical coupling, the maximum efficiency of the frequency conversion in TMs can be achieved, when the contributions of radiative and nonradiative loss mechanisms coincide.
Moreover, based on the concept of high-order topological insulators, a hybrid metal–dielectric TM with symmetric honeycomb lattices was recently proposed to enhance the intensity and robustness of THG [218]. Since the topological edge and corner states can not only enhance light intensity but also offer a robust protection of light against disorder and defect perturbations, a significantly enhanced THG has been experimentally observed. As shown in Fig. 13(c), such a remarkable improvement can be used to develop a nonlinear imaging technique, which enables a high-resolution and background-free photograph of states.
FWM is an intermodulation process in nonlinear optics, and it is characterized by the third-order nonlinear susceptibility of a nonlinear material, similar to the case in THG. However, the difference is that the frequencies of the three pump photons are not the same. In FWM nonlinear interaction, two or three frequencies generate one or two new frequencies. The confined edge or corner light modes can significantly enhance the strength of the FWM nonlinear process. For example, a plasmonic QH TM consisting of a periodic array of nanoholes in a graphene sheet was proposed to study the topological protection and enhancement of FWM interactions [221]. As demonstrated in Fig. 14(a), the QH effect is realized by breaking the TR symmetry via externally applying a static magnetic field. Due to the significant nonlinearity enhancement and long lifetime of graphene plasmons along the topological edge states, a net gain of FWM interaction can be achieved with an ultralow pump power of less than 10 nW, which is a consequence of the unusually large effective nonlinear edge-waveguide coefficient . It is more than 10 orders of magnitude larger than that of commonly used silicon PhC.
![]()
Figure 14.Four-wave mixing (FWM) in active topological metasurfaces. (a) FWM of topologically protected one-way edge plasmons in a graphene QH topological metasurface [221]. (b) Generation of indistinguishable photon pairs via spontaneous FWM in an anomalous QH topological metasurface [219]. (c) Entangled photons emerge and flow at a pair of edge modes in a silicon anomalous Floquet topological metasurface [107].
In addition to theoretical studies, some important experimental results have been reported recently. For instance, an anomalous QH TM consisting of coupled ring resonators is reported to generate indistinguishable photon pairs via spontaneous FWM [219]. Due to the linear dispersion of topological edge states, a phase-matched generation of photon pairs throughout the edge band can be easily achieved. Thus, by tuning the input pump frequencies in the edge band, the spectral–temporal bandwidth of photon pairs can be engineered. Since the anomalous QH TM is a TR symmetric system, it supports two spin-locked topological edge states, as shown in Fig. 14(b). Such counterpropagating topological edge states can be used to generate path entanglement and split the indistinguishable photon pairs. Furthermore, entangled states are generally sensitive to the disorder or defect in optical devices, whereas topological states are naturally robust against fabrication perturbations. Thus, it has great potential for generating topologically protected entanglement via FWM. Recently, based on the complementary metal–oxide–semiconductor (CMOS) fabrication technique, a silicon anomalous Floquet TM has been proposed to experimentally demonstrate the robustness of a topological photonic entanglement against certain imperfections [107]. As depicted in Fig. 14(c), the anomalous Floquet TM consists of a square lattice of coupled silicon ring resonators, and supports two counterpropagating edge states with identical spectral distribution. To demonstrate the robustness of topological photonic entanglement, some imperfections have been introduced by adding or removing a single ring or an entire unit cell in the ring lattice structure. The experimental results prove that topological edge states can be used to protect photonic entanglement in the presence of structure defects.
HHG is a nonlinear interaction between an intense light and nonlinear materials to generate new photons with high harmonic frequencies, which are generally above fifth harmonic. Recent studies find that TM is a particularly fertile platform for the study of HHG. For example, an amorphous silicon BIC TM has been designed to generate the third- and fifth-harmonic optical vortices [225]. In the linear regime, when the TM is illuminated by a circularly polarized Gaussian beam, it generates only an opposite-handedness transmitted beam with a certain topological charge. But in the nonlinear regime, under the same excitation condition, the same TM can generate THG and fifth-harmonic generation (FHG) signals, which enables the harmonic optical-vortex generation of both handednesses, as shown in Fig. 15(a). Moreover, the simulated results show that the topological charges in the nonlinear case are related to the order of harmonic signals. In addition to the symmetric BIC effect, an asymmetric BIC TM has also been proposed to study HHG [224]. To support BICs, a pair of rectangular silicon bars in each unit cell is optimized to break the in-plane symmetry, and an asymmetry parameter is defined, as shown in Fig. 15(b). The corresponding results prove that the radiative and quality factors of the quasi-BIC are highly dependent on the asymmetry parameter. By illuminating intense laser pulses on the asymmetric TM, the generation of optical harmonics up to the 11th order can be experimentally measured. The experimental results also prove that HHG is highly dependent on the pump polarization and pulse duration.
![]()
Figure 15.High-harmonic generation (HHG) and Kerr effects in active topological metasurfaces. (a) High-harmonic optical vortex generation in a symmetric BIC topological metasurface [225]; (b) 3rd to 11th optical harmonics generated in a nonlinear and asymmetric BIC topological metasurface [224]. (c) Power-dependent corner states and solitons in high-order topological metasurfaces [229].
Different from aforementioned frequency conversions, the Kerr effect is a special nonlinear process, as there is only a nonlinear change in the refractive index of a material, without any generation of new frequencies. In fact, the Kerr effect includes the electro-optic Kerr effect, also called direct-current (DC) Kerr effect, and the optical Kerr effect, also known as the alternating-current (AC) Kerr effect. It is generally characterized by the real part of the third-order susceptibility, whose imaginary part indicates a nonlinear absorption, namely, optical saturable absorption. The Kerr effect in active TM has promising potential applications for all-optical modulators, optical solitons, etc. For instance, a high-order TM has been designed to experimentally demonstrate nonlinear corner states as well as the formation of solitons [229]. As shown in Fig. 15(c), the high-order TM is constructed by a kagomé lattice of fused silica waveguides. When the strength of the intra-cell bond exceeds that of the inter-cell bond , namely, , the light modes are trivial. But, when , there are some nontrivial states, also called topological states, including topological edge and corner states, which can be verified by corresponding field distributions. To study the nonlinear Kerr effect, an intense ultrashort laser with enough peak power is used to illuminate the corner sites of the TM to elicit a nonlinear Kerr response. In the linear regime, a linear light excitation (0.2 MW cm) penetrates deeply into the TM. By increasing the input power to 2.5 MW cm, due to the nonlinear Kerr response in the TM, the light mode is confined to the corner to form a tightly localized soliton. These findings pave the avenue towards the development of nonlinear compact devices.
2. Topological Laser
Lasers, as the most representative active devices, have been extensively studied in different kinds of photonic cavities. However, those photonic cavities are usually sensitive to defects, disorders, and fabrication imperfections and suffer from device-to-device performance, which imposes a fundamental constraint on the applications of lasers. Lasers built on topologically robust cavities have, therefore, been highly desired ever since the invention of lasers.
The first experimental demonstration of topological lasers in QH TM was reported in Ref. [231], where the nonreciprocal single-mode lasing from topological cavities of arbitrary geometries was designed at room temperature and at telecommunication wavelengths. The nonreciprocal topological laser was implemented by two PhCs with distinct topological invariants. Despite the narrow magneto-optically induced photonic bandgap, a robust topological cavity mode in an arbitrarily shaped cavity and topological lasing can be observed with a significant isolation ratio as large as 11.3 dB from the oppositely propagating mode. However, since the magneto-optic effect is very weak at optical frequencies, only a narrow topological bandgap is produced. To enlarge the topological bandgap, another all-dielectric TM based on artificial magnetic fields is theoretically proposed and experimentally demonstrated [253,235], as shown in Fig. 16(a). It possesses a sizable topological bandgap and operates under optical pumping and at cryogenic temperatures.
![]()
Figure 16.Topological laser based on active topological metasurface. (a) Topological laser in a QH topological metasurface consisting of honeycomb lattice of coupled ring resonators [253]. (b) Electrically pumped topological laser in a QSH topological metasurface comprising a square lattice of ring cavities and link resonators [242]. (c) Topological bulk laser in a QSH topological metasurface based on band-inversion-induced reflection [241]. (d) Electrically pumped topological laser based on QVH effect operating at terahertz frequencies [237]. (e) Low-threshold topological laser in a second-order topological metasurface [238]. (f) Lasing improved by BICs [232].
The applications of QSHE have been extended to construct topological cavity lasers by using topological edge states with a spin-momentum locking property. Shao
More recently, an electrically pumped topological laser under room temperature was developed [242], as shown in Fig. 16(b). This TM consisted of a periodic array of resonators coupled through an aperiodic set of auxiliary link structures to mimic the QSHE; thus it can generate topologically protected lasing and exhibit single frequency emission. Apart from lasing to topological edge/interface modes, topological properties based on bulk states could also be used to realize topological lasing. In such a topological bulk laser [241], the TM shows topological band inversion around the Γ point between its interior and cladding area. As shown in Fig. 16(c), due to band inversion, the wave functions of bulk states in topologically trivial and nontrivial areas have opposite parities. As a result, in-plane light waves in the trivial region cannot propagate into the nontrivial region, and they are reflected at the interface forming an effective cavity feedback. Furthermore, band-inversion-induced reflection occurs only around the point, which provides a novel lasing mode selection mechanism and enables directional lasing emission of cavity modes.
It has also been demonstrated that valley-Hall PTIs can be utilized to construct topologically robust cavities by creating a domain wall in a closed form [236,237,256,257]. For example, a topological cavity can be applied to devise electrically pumped THz quantum cascade lasers (QCLs), which are widely used in communication, imaging, and sensing in the THz domain [237]. As shown in Fig. 16(d), the laser cavity is a triangle loop supporting robust valley kink states, and the yellow region is electrically pumped. With an electrical injection, the running-wave mode in the cavity is lasing and distributes uniformly around the domain wall even in the presence of defects and sharp corners. The robust laser based on valley kink states was also realized at optical frequencies. Moreover, room-temperature lasing with a narrow spectrum, high coherence, and threshold behavior was experimentally observed in this laser. Interestingly, the emitted beam exhibits a singularity encoded by a triade cavity mode that locates at the three corners of the cavity [257].
Due to the small footprint (small mode volume and high quality factor), a second-order topological corner state has also been exploited for topological lasing [238,239,257,258]. In Ref. [238], the first experimental observation of a topological nanolaser in a 2D topological PhC nanocavity, exploiting the Wannier-type 0D corner state at the nanoscale, was demonstrated, as in Fig. 16(e). In Ref. [258], topological lasing was observed at all hierarchical eigenstates, i.e., 2D bulk, 1D edge, and 0D corner states in a 2D PhC platform with a square area of a topologically nontrivial PhC structure surrounded by a topologically trivial counterpart. Furthermore, multiple corner states and their interactions have also been observed, e.g., in Ref. [257], triade mode lasing, in which three corner modes are coupled to each other and exhibit lasing action, was observed at the nanoscale and room temperature in a valley-Hall nanophotonic cavity embedded into 2D topological lattices with semiconductor quantum wells as a gain medium.
BICs have manifested superiority in boosting lasing performance by reducing the lasing threshold and miniaturizing the size of lasers. Although many surface-emitting lasers [259–263] are based on symmetry-protected BICs, the first announcement of BIC lasing is demonstrated by Kodigala
B. Reconfigurable Topological Metasurface
Generally, there are two major constraints of the unreconfigurable TM. (1) The space utilization ratio, namely, the ratio of the edge region to the bulk region, of most passive TMs, is very low. Specifically, since topological modes (such as edge mode, corner mode) exist only at the boundary or corner, most regions (such as bulk regions) of TM are wasted, hindering the high-density opto-electronic integration. Owing to the reconfigurable functionality of active TM whose light propagation route can be reconfigured on demand inside the bulk region, its space utilization ratio can be significantly improved, leading to high-density photonics routing. (2) The optical performances of passive TMs are fixed once the device has been fabricated. However, for many practical applications, the reconfigurability and tunability of light manipulation are essential. For instance, multiple photonic topological functionalities are expected to be achieved in a single but reconfigurable PTI, so that the time and costs associated with the design and fabrication process can be reduced. Currently, the reconfigurable manners of TMs include electrical control, optical control, mechanical control, and thermal control, as listed in Table 2. Typical Reconfigurable Manners in Active Topological Metasurface Aluminum-doped zinc oxide (AZO); Su–Schrieffer–Heeger (SSH) model; liquid crystal (LC); higher-order topological insulators (HOTIs); transistor switch (TS); vanadium (IV) oxide (Mechanism Platform Medium Frequency Tuning Time Result Refs. Electrical QVH Graphene 28.3 THz / Sim [ QSH LC 0.44 c/a / Sim [ QVH / Sim [ QVH LC / Sim [ QVH PIN 7.2 GHz Exp [ QH LC / / Sim [ HOTIs LC / Sim [ QVH LC / Sim [ Floquet TS 0.5 GHz 2 ns Exp [ Optical Floquet AZO / Sim [ QVH Si Exp [ Non-Hermitian InGaAsP 202 THz (1.486 / Exp [ BIC 543 THz (0.552 Exp [ Mechanical QSHE Metallic Exp [ SSH Dielectric / Sim [ QSHE Si 0.46 c/a / Sim [ QSHE Dielectric / Sim [ Thermal QSHE Exp [ Floquet TiN 230 THz (1.305 / Sim [ HOTIs 194 THz (1.55 Sim [ QVH 0.16 THz / Sim [
So far, the electrically reconfigurable manners of TMs have been mainly studied theoretically, and there are few experiment reports in which the operating frequencies are all in the microwave regime. The most explored physical effect in current reconfigurable TMs is the QVH effect.
In the microwave regime, it is relatively convenient to integrate active lumped elements (such as PIN and other transistors) into TM to implement an electrically reconfigurable functionality. For example, You
![]()
Figure 17.Electrically controlled reconfiguration in topological metasurfaces. (a) Ultrafast reprogrammable plasmonic topological metasurface based on QVH effect [269]. (b) Chip-scale Floquet topological metasurface based on switched-capacitor networks [273]. (c) Reconfigurable QSH topological metasurface based on liquid crystal [266]. (d) HOTI topological metasurface supporting edge-corner state switching [271].
In addition to the lumped element, some other electro-optical materials (such as graphene, BaTiO3, LC) can also be used to implement electrical control of TMs. For example, since the Fermi energy of graphene can be tuned electrically, a mid-infrared TM in metagated-tuned graphene was proposed to enable rapid switching of topological plasmons via simple electric gating [265]. LC is another popular phase-change material widely used to implement electronically controlling TM, as the anisotropic permittivity of LC is tunable under different bias voltages. As shown in Fig. 17(c), based on the QSHE, a TM consisting of silicon pillars surrounded by an LC was studied [266]. The TM is enclosed between conducting electrodes, and it can be switched by applying voltage to the electrodes, as the refractive index of LC would be changed when the voltage is applied.
Recently, it was reported that corner states can also be electrically controlled by LC [271]. As shown in Fig. 17(d), a dynamically tunable and reconfigurable TM is realized in HOTIs by changing the loading voltage of the LC. In this reconfigurable TM, its edge and corner states can be switched at the same frequency. In addition to HOTIs, a tunable and programmable valley TM based on nematic LCs has also been reported [272], and its inversion symmetry breaking and topological transition are implemented through electrically controlling the relative permittivity of LC cells. Moreover, this valley TM can be discretized to a number of supercells, each of which is coded with “0” or “1” to realize a programmable functionality.
Optically controlled reconfigurable light propagation routes in TMs were reported in Refs. [240,274–276]. For instance, based on tunable transparent conducting oxides (TCOs) and standard SOI waveguide technology, a Floquet TM has been theoretically developed to achieve ultrafast all-optical control of topological states [274]. As depicted in Fig. 18(a), the unit cell of the proposed TM consists of four ring resonators and four link couplers, which have been covered with aluminum-doped zinc oxide (AZO). AZO is a typical kind of TCO materials, and its refractive index is sensitive to pump light. Therefore, an ultrafast control over the mode index of link couplers can be realized by switching on or off the pump light, leading to all-optical control of topological states in a Floquet TM. In addition to theoretical results, based on the QVH effect, an SOI TM with an optically controlled reconfigurable functionality has been experimentally studied recently [275]. The tunability is enabled by the free-carrier excitation initiated by the pump beam, leading to reduction of the real part of the refractive index and increase of the imaginary part of the refractive index in silicon. As shown in Fig. 18(b), fast refractive index modulation could be used to switch the topological light propagation, and the corresponding switching time is up to the order of nanoseconds.
![]()
Figure 18.Optically controlled reconfiguration in topological metasurfaces. (a) All-optical control of topological states in a Floquet topological metasurface [274]. (b) Transmission modulation in a QVH topological metasurface by optically tuning the refractive index of silicon [275]. (c) Optically reconfigured topological edge states by breaking local non-Hermitian symmetry [276]. (d) Ultrafast all-optical switching between the vortex beam lasing and linearly polarized beam lasing [240].
In addition to silicon, InGaAsP can also be used to construct optically controlled TM. As an example, a non-Hermitian TM was proposed recently based on optical modulation [276]. As demonstrated in Fig. 18(c), the TM consists of coupled microring resonators, and optical control is realized by illuminating a laser on the InGaAsP metasurface to create gain (pumping region) and loss (no pumping region) domain walls, where topological states can be observed. In this way, optical control can be used to actively steer the topological light propagation route by projecting a spatial pumping pattern onto the TM. The direction of vortex lasers is steerable by tuning BICs in momentum space, as shown in Fig. 18(d). Huang
Mechanically controlled reconfigurable electromagnetic pathways in TMs were reported in Refs. [40,277–279]. Based on the QSHE, a reconfigurable TM has been experimentally studied between two parallel copper plates [40]. To implement the mechanically controlled reconfigurable functionality, a periodic triangular array of metallic rods with ring collars drills holes on the parallel copper plates, as illustrated in Fig. 19(a). By mechanically moving the rods up or down, a reconfigurable electromagnetic pathway between two topologically distinct domains can be created on demand.
![]()
Figure 19.Mechanically controlled reconfiguration in topological metasurfaces. (a) Robust reconfigurable microwave propagation routes in a QSH topological metasurface [40]. (b) Tunable edge states in a split-ring topological metasurface [278]. (c) Reconfigurable topological metasurface based on honeycomb lattice of rotating dielectric cuboids [279].
Split-ring structures can also be used to construct a mechanically controlled reconfigurable TM [278]. As shown in Fig. 19(b), since the topological band diagrams depend on the rotation angle of the split-ring unit, a tunable topological state can be achieved by mechanically controlling the rotation angle to introduce two topologically distinct phases. Similar mechanical control in reconfigurable TM has also been implemented theoretically in a honeycomb lattice with dielectric cuboids [279]. Specifically, the unit cell of the designed TM consists of six dielectric cuboids with a rotation angle. By mechanically rotating the six cuboids around their own centers, a radial or circular structure in each unit cell can be constructed to open or close the topological bandgap, as demonstrated in Fig. 19(c). As a consequence, the light propagation routes can be mechanically reconfigured in the proposed TM.
Thermal control is another important approach to construct a reconfigurable light propagation route in TM [280–283]. Based on the QSHE, a dynamically reconfigurable edge state in TMs has been experimentally studied [280]. By changing a thermal phase-change material, namely, , between amorphous and crystalline, the refractive index of the pillar unit can be thermally modulated, leading to a reconfigurable topological edge state, as shown in Fig. 20(a). It demonstrates that the TM can quickly switch the topological light propagation in 150 ns.
![]()
Figure 20.Thermally controlled reconfiguration in topological metasurfaces. (a) Dynamically reconfigurable topological edge state in a thermally controlled topological metasurface [280]. (b) Thermally controlled topological metasurface based on silicon-on-insulator technology [281]. (c) Thermally controlled edge and corner states in HOTI topological metasurfaces [282].
![]()
Figure 21.Quantum information applications of topological photonics. (a) Topological source of quantum light in a coupled array of ring resonators [220]. (b) On-chip Hong–Ou–Mandel interference in a topologically protected valley-dependent quantum circuit [288]. (c) Topological protection of biphoton states in a nanophotonic platform [289]. (d) Topologically protected entangled photonic states in a nanophotonic platform with two topological defects [290]. (e) Topologically protected energy–time entangled biphoton states in spin-Hall topological photonic crystals [291]. (f) Topologically protected polarization quantum entanglement on a photonic chip [292].
Thermally controlled edge states can also be realized in a Floquet TM [281]. As demonstrated in Fig. 20(b), its unit cell includes four “site” ring resonators and four “link” ring couplers. The couplers are made of silicon and covered with thermal modulators. Based on the thermo-optic effect in silicon, the accumulated phase of light propagating through the rings can be modified to control the topological edge states. In addition to thermally controlled edge states, a tunable and reconfigurable high-order topological state in TM with phase change materials, namely, and , has also been thermally controlled [282]. More specifically, an SSH-like square TM is optimized. As depicted in Fig. 20(c), its outer region consists of topological trivial unit cells, whereas its inner region is filled with topological nontrivial unit cells. Since the refractive index of phase change materials is sensitive to temperature, the topological edge state and topological corner state at the same frequency can be switched relatively fast.
4. BEYOND
Exploring and harnessing quantum mechanical effects for future technological applications has attracted ever-increasing attention in recent years. However, in most cases, quantum features of materials are quite fragile and susceptible to structural as well as environmental changes and require stringent conditions for their quantum properties to maintain, e.g., it is well known that entangled states are fragile with respect to decoherence in a noisy environment. This fragility of quantum states is particularly relevant for quantum photonic states in nanophotonic structures where small fabrication imperfections are unavoidable, and these imperfections can have a detrimental impact on the quantum information encoded in photonic states. As the system properties of topological matters depend only on the global properties (topological invariants) of the system, where local defects and imperfections will have no effect on the system properties, the concept of topology could provide a promising route to design highly robust quantum photonic devices with built-in topological protection, whose quantum properties can be much easier to maintain. Thus it is particularly interesting to apply topological concepts to protect the fragility of photonic states in the quantum regime [284,285].
In this section, we discuss how topological photonics can advance the study of quantum optics. We first show how topological photonic systems can protect single or multi-photon states, which has great potential for fault-tolerant on-chip quantum information processing and computing. We then discuss how quantum emitters could be interfaced with electromagnetic environments for creating topological quantum metamaterials with applications ranging from scalable quantum networks to strongly interacting topological phases of light.
A. Quantum Information in Topological Metasurfaces
In the quantum regime, vacuum fluctuations of electromagnetic fields can be modified by the topological band structures of photonic systems. To show this, the authors of Ref. [286] considered a Hamiltonian with particle nonconserving terms that can coherently add and remove pairs of particles from the system and demonstrated the existence of a situation where the topologically protected chiral edge modes in a system with boundaries are unstable, whereas all bulk modes are stable. Exploiting this exotic feature, the authors further showed that a topologically protected, quantum-limited traveling wave parametric amplifier can be realized. By manipulating the structure and vacuum fluctuations of topologically robust electromagnetic edge modes realized in a 2D array of ring resonators under a uniform synthetic magnetic field emulating the integer QHE, the authors of Ref. [220] [Fig. 21(a)] experimentally realized a topological source of quantum correlated photon pairs via spontaneous FWM in which the spectral correlations between signal and idler photons are robust against fabrication disorder and outperform a similarly designed topologically trivial source of correlated photons. In particular, to characterize the nontrivial correlations between generated photons, the authors measured the second-order cross-correlation function to detect signal and idler photons separated by time and observed a maximum at . Furthermore, using a Hanbury-Brown–Twiss setup, the authors measured the conditional (heralded) autocorrelation function for signal photons, conditioned on the detection of idler photons and observed a conditional , indicating that the photons are anti-bunched [note that classical light sources are characterized by , whereas quantum light sources, such as single photons, are distinguished by ]. These interesting results open a route towards on-chip, scalable sources of heralded and entangled photons with identical spectra, which are promising for applications in quantum information processing and quantum communications.
Single photons emitted by quantum light sources are essentially indistinguishable, which can result in quantum interference. The authors later [219] demonstrated a tunable source of indistinguishable photon pairs using dual-pump spontaneous FWM in a similar 2D array of resonators emulating anomalous QHE, i.e., in a configuration where while the magnetic flux through a single plaquette is non-zero, the average magnetic flux through a unit cell of two plaquettes of the lattice is zero. In this dual-pump spontaneous FWM process, two pump photons at different frequencies annihilate and create two frequency-degenerate photons, called the signal and idler, which are indistinguishable. Hong–Ou–Mandel (HOM) interference between the indistinguishable photon pairs was successfully demonstrated with an HOM dip of visibility reaching 88(10)%. A novel feature of the indistinguishable photon pairs generated in this setup is that their spectral–temporal bandwidth can be tuned by the input pump frequencies in the edge band and the generated photon pairs are energy–time entangled. Quantum interference of topological states of light has also been experimentally observed in integrated photonic circuits using coupled waveguide arrays [287] and valley-dependent quantum photonic circuits [288]. Especially, the authors of Ref. [287] implemented the off-diagonal Harper model using an array of coupled waveguides that exhibits topological boundary states. Two single-photon topological boundary states, initially at opposite edges of a coupled waveguide array, are brought into proximity, where they interfere and undergo a beam splitter operation. HOM interference with visibility was observed in the experiments, confirming the non-classical behavior of topological photonic states. Exploiting photonic valley states in a valley-dependent photonic platform, the authors of Ref. [288] [Fig. 21(b)] demonstrated two-photon HOM interference with a high visibility of 95.6(0.6)%. The valley photonic platforms are CMOS compatible, scalable, and much more integrated, providing a novel method for the on-chip valley-dependent quantum information process.
Topological photonic states can also protect the quantum features of photons, such as single-photon quantum states [293], squeezed light [294], and two-photon quantum correlations [289,295,296]. The authors of Ref. [293] demonstrated that the quantum features of single photons can be protected in topological structures against diffusion-induced decoherence in coupled waveguides and noise decoherence from the ambient environment. Specifically, the authors considered a silica photonic chip of laser written waveguides implementing the “off-diagonal” version of the Harper model and injected heralded single photons into topological boundary states. To study whether the topological nontrivial boundary state can preserve the single-photon feature after the single photon goes out from the lattices, the authors measured the second-order anticorrelation using a Hanbury-Brown–Twiss interferometer and found that the second-order anticorrelation parameter has no distinct changes before and after the photonic chip, confirming that the single-photon features can be well preserved.
Topological protection of squeezed light on a photonic chip was also demonstrated in Ref. [294], where the waveguide in the topologically protected lattice functions as an FWM source in which glass absorbs two photons from the pump wave, and generates signal and idler photon pairs. To test whether the on-chip generated correlated photons can also be protected, the authors measured the cross-correlation function of the correlated photon pairs and found that the topologically protected structure can provide nearly five times higher cross-correlation values than those in unprotected states. Furthermore, the squeezing parameters of the topologically protected channels are larger than those of unprotected channels, indicating that the squeezed states can be well protected in the topological structure. Moreover, topology states can also protect biphoton states, e.g., the authors of Ref. [289] [Fig. 21(c)] considered a topological lattice of a silicon nanowire array on a silica substrate and demonstrated experimentally the robustness of the spatial features and propagation constants of biphoton states. Exploiting a topological lattice fabricated in a borosilicate glass via the femtosecond laser direct writing technique, the authors of Ref. [295] experimentally demonstrated the topological protection of two-photon quantum states against decoherence, where by measuring the quantum correlation of two photons from the topologically nontrivial boundary state, a high cross-correlation and strong violation of Cauchy–Schwarz inequality up to 30 standard deviations was obtained. The authors further showed that topological protection is robust to the wavelength difference as well as distinguishability of two photons by preparing different quantum sources. Two-particle quantum correlations of indistinguishable photons were also studied experimentally in Ref. [296], where the authors found that the existence of the edge state at the topological edge in the SSH model has a significant influence on the quantum interference of indistinguishable photons.
As the most counterintuitive quantum non-local correlations and an important resource of quantum information, computation, and communications, quantum entanglement could also be protected by topology, which could be exploited for robust propagation of quantum information in disordered systems as demonstrated both theoretically [291,297] and experimentally [290,292,298] recently. In Ref. [297], the authors studied the transport of time–bin entangled photon pairs in coupled ring resonators simulating the integer QHE and found that while the transport through edge states preserves temporal correlations of entangled photons, the transport through bulk does not preserve these correlations and can lead to significant unwanted temporal bunching or anti-bunching of photons. They further studied the transport in the presence of disorder and found that while the edge transport remains robust, enhanced bunching/anti-bunching of photons is a key feature for the bulk transport. Topological protection of entangled biphoton states has also been studied in valley PhCs [223], where the authors studied nonlinear FWM interaction of topological valley kink states propagating along the interface between two valley PhCs and demonstrated that the signal and idler photons generated from the FWM interaction are not only continuously frequency entangled, but also robust against sharp bends and scattering, indicating topological protection of entangled photon pairs. Later, the authors of Ref. [291] [Fig. 21(e)] studied the quantum correlation between signal and idler photons generated from the FWM process in topological PhCs emulating the QSHE and found that the generated signal and idler photons are energy–time entangled, i.e., entangled between the frequencies of photon pairs and their time of arrival. Furthermore, the topological edges states of pump, signal, and idler photons are robust against sharp bends and defects, indicating that the energy–time entangled biphoton states are topologically protected.
Experimentally, topologically protected entangled photonic states have been studied in photonic chips with coupled waveguides [290,292,298]. The first experimental demonstration of topological protection of entangled biphoton states was reported in Ref. [290], where the authors considered a photonic chip of coupled silicon nanowires on a silica substrate, and entangled biphoton states were generated via spontaneous FWM (SFWM) within the photonic chip itself. By studying the biphoton correlation map at the output of the topological lattices with different levels of deliberately introduced disorder, the authors demonstrated that the entanglement of biphoton states can be well preserved against disorder that respects the chiral symmetry of the system. Biphoton entanglement of photonic modes of two different topologies was studied in Ref. [298] [Fig. 21(d)], where the authors considered a bipartite array of SOI waveguides in which nonlinearly generated photon pairs are created in a superposition of three colocalized modes of two distinct topologies (both trivial and nontrivial). They also studied the average relative weight of the topological and trivial components of the entangled state when increasing levels of disorder and found that at low levels of disorder, the population probability of trivial biphoton modes is higher than that of the topological mode, whereas at strong disorder, the population probability of the topological biphoton mode is higher than that of any of the hybrid trivial modes. As a result, due to the coexistence of topological and trivial biphoton modes in such entanglement, the measured entangled biphoton state does not preserve its shape under the presence of off-diagonal disorder. Recently, the topological protection of two-photon polarization entangled states was studied in a photonic chip made of a coupled waveguide array [292] [Fig. 21(f)]. Employing the process of the tomography technique, the authors demonstrate that quantum entanglement can be well preserved by topological states even when the chip material introduces disorder and relative polarization rotation in phase space.
B. Topological Metasurface Interfaced with Quantum Emitters
The interaction of quantum emitters with photonic environments plays an important role in quantum systems engineering, e.g., it can be used to build quantum metamaterials, where the fundamental building blocks of artificial optical materials are quantum coherent entities and electromagnetic modes of the system, and importantly, the quantum coherence of these artificially engineered materials can maintain a time longer than the traversal time of the relevant electromagnetic signal. Controllable interaction between quantum emitters is also an essential ingredient for the realization of scalable quantum networks, where each quantum node can be a hybrid of photon and quantum emitters, as photons can serve as flying qubits to transmit information, whereas quantum emitters can be used as local qubits to store information. Moreover, due to the inherent nonlinearity of constituent quantum emitters, integrating quantum emitters into topological photonic structures can not only allow the study of light–matter interactions in topologically nontrivial environments, but also provide an intriguing opportunity for exploring strongly correlated states of light. Thus, how quantum emitters will couple with the various topological photonic platforms has attracted great attention recently.
In Ref. [46], the authors experimentally demonstrated chiral coupling between a quantum emitter and the helical topological edge mode at the boundary of two distinct topological PhCs emulating the QSHE. As shown in Fig. 22(a), the authors considered a thin GaAs membrane with epitaxially grown InAs quantum dots (QDs) at the center acting as quantum emitters. Under a magnetic field that induces a Zeeman splitting in the QD excited state, two nondegenerate states that emit with opposite circular polarizations can couple to the helical topological edge modes, and the emitted single photons exhibit robust transport, even in the presence of a bend.
![]()
Figure 22.Coupling of a single quantum emitter to topological photonic systems. (a) Chiral coupling between the helical topological edge modes of spin-Hall topological photonic crystals and a quantum emitter [46]. (b) Chiral topological photonics with an embedded quantum emitter in a valley-Hall topological photonic crystal waveguide [301]. (c) Coupling between a quantum emitter and second-order topological corner state for cavity quantum electrodynamics [302].
Quantum emitters can also be used to probe the topological modes of photonic structures as demonstrated in Ref. [299], where the authors fabricated topological ring resonators in a spin-Hall-type topological PhC platform and by using spatially resolved PL measurements, topological modes confined to the PhC interface were visualized. However, as the band inversion point in spin-Hall topological waveguides happens around , the topological edge modes in these slab platforms have radiative coupling to free-space modes. To avoid this radiative loss, a valley-Hall topological photonic interface could be exploited, as the topological valley edge modes lie below the light line. In Ref. [300], a valley PhC waveguide in a GaAs slab was experimentally characterized by the near-infrared light emitted from the InAs QDs inserted at the middle of the slab layer as an internal light source.
Robust wave propagation against sharp bends was further observed by PL images from QDs. Employing an interface between two valley-Hall topological PhCs, a topological resonator in the shape of a super-triangle was studied in Ref. [303], where chiral spontaneous emission with the direction of emission depending on the polarization of the emitted light was demonstrated. More specifically, QDs excited by external pump sources are coupled with a topological resonator that supports two counterpropagating modes with opposite chiralities. By exciting the QDs and collecting the emission from the ends of the waveguide through grating couplers, it was experimentally observed that the quantum emitter emits preferably into one of the counterpropagating edge modes depending upon the spin of the pump source. Collecting the PL signal at the left grating coupler, a single branch of the Zeeman split QD spectrum was clearly observed, which was a signature of chiral coupling. Furthermore, Purcell enhancement of emission due to the strong coupling between the quantum emitter and topological resonator was also achieved when tuning the quantum emitter into resonance with the topological resonator by a magnetic field.
In another work [301], a chiral quantum optical interface using semiconductor QDs embedded in a valley-Hall topological PhC waveguide was also realized, where chiral coupling of single QDs to the nontrivial waveguide mode with a spin-dependent, averaged directional contrast of up to was demonstrated. As demonstrated in Fig. 22(b), chiral coupling of a QD with a photonic ring resonator in the form of a triangle with three 120° corners was also demonstrated, where the resulting experimental PL map was used to reveal the distinct triangular shape of the full waveguide. It also shows that the direction of emission into the waveguide relies on the dipole polarization, when a QD is located at the domain wall. Moreover, the measured PL signal verifies the chiral characteristics for the topologically protected ring resonator modes.
Most recently, an integrated topological add–drop filter consisting of a compact resonator coupled to a pair of access waveguides, was experimentally realized within a valley-Hall topological PhC [304]. The authors demonstrated chiral emission from a QD embedded within the resonator by showing that while one spin state of a QD transition couples into two of the four output ports of the device, the orthogonal spin state couples to the other two output ports. Slow light waveguides are preferable for high-performance single-photon sources, as slow light modes can enhance light–matter interactions and thus accelerate the emission of quantum emitters into the modes via the Purcell effect.
Recently, single-photon sources using single QDs embedded in topological slow light waveguides based on valley PhCs were reported in Ref. [305], where the authors observed that single QDs coupled to the topological slow light waveguide exhibit large Purcell enhancement of a spontaneous emission rate up to a factor of with a group index over 20. To confirm the single-photon nature of QD emission, the authors further performed intensity autocorrelation measurements using a Hanbury-Brown–Twiss setup, and clear antibunching behavior was observed. Apart from coupling to the topological photonic edge modes, QDs have also been coupled to second-order corner states as demonstrated in Fig. 22(c) [302], where enhancements of PL intensity by a factor of about four and emission rate by a factor of 1.3 are both observed when the QD is on resonance with the corner state. Furthermore, the existence of topological corner and edge states with high Q was also observed by PL spectra. The realization of a coupled quantum emitter with a topological corner state enables the application of topology into a cavity quantum electrodynamics setup.
Apart from the coupling of a single quantum emitter to topological photonic modes, strong coupling and entanglement between emitters can also be achieved via coupling to the same topological photonic mode. Recently, the authors of Ref. [306] theoretically studied a PhC platform supporting both topologically protected edge states and 0D topological corner cavities. When quantum emitters are put into topological cavities, the strong coupling between them can be fulfilled with the assistance of the topologically protected edge state. Such strong coupling can maintain a very long distance and be robust against various defects. Moreover, the duration of quantum beats for such entanglement can reach several orders longer than that for entanglement in a conventional photonic cavity, making it beneficial for a scalable quantum-information process.
Most recently, topologically protected entanglement emitters were realized experimentally in a monolithically integrated plug-and-play silicon photonic chip in ambient conditions [107], as shown in Fig. 23(a). Exploiting the intrinsic FWM nonlinearity of silicon waveguides, the system emits a topological Einstein–Podolsky–Rosen (EPR) state, which was demonstrated to be topologically protected against artificial structure defects by comparing the state fidelities of and for perfect and defected emitters, respectively. The authors further verified the topological EPR entangled states by tomographic measurement and Bell violation, and verified the topological multiphoton NOON (i.e., N particles in mode a, and 0 particles in mode b, vice versa) entangled states by interferometric measurement of the de Broglie wavelength.
![]()
Figure 23.Multiple quantum emitters in structured photonic environments for engineering of topological quantum metamaterials. (a) Topologically protected quantum entanglement emitters in a coupled array of ring resonators [107]. (b) 1D array of quantum emitters coupled to the chiral edge state of a topological photonic crystal [307]. (c) Topological quantum optics using 2D array of quantum emitters coupled to a photonic crystal slab [310]. (d) 2D array of quantum emitters embedded in a photonic cavity [311].
Coupling a 1D array of quantum emitters to the chiral photonic edge state allows the creation of strongly correlated states of photons in a highly controllable way. In Ref. [307], the authors showed that photons in such a chiral channel interacting with an ensemble of quantum emitters can produce outgoing states with robust, controllable, and universal properties originating from the topological nature of the edge state, as illustrated in Fig. 23(b). In particular, they found that the outgoing photonic wave function does not contain any information about the positions of emitters; its nodes are rather determined by universal numbers—the zeros of Laguerre polynomials. In the case of two-photon scattering, they observed a clearly pronounced parity effect with respect to the number of emitters, which manifests in a transition from photon bunching to antibunching as one changes the parity of the number of emitters from even to odd.
Further arranging the quantum emitters into regular 2D arrays can be used to build the quantum metasurface [308], in which quantum-operator-valued reflectivity can be used to control both the spatiotemporal and quantum properties of transmitted and reflected light. In Ref. [309], the authors studied a 2D honeycomb array of closely spaced quantum emitters and found that the system maintains topologically protected confined optical modes that are immune to large imperfections as well as to the most common loss processes such as scattering into free-space modes and spontaneous emission. Such modes can be used to control individual atom emission, and to create quantum nonlinearity at a single-photon level, which could lead to strong interactions between individual excitations. However, to realize such topologically protected confined optical modes requires deep subwavelength interatomic spacing, which may be challenging to implement experimentally.
Later, the authors [310] considered a triangular lattice of a quantum emitter array integrated with a 2D PhC slab of air holes where the emitters can interact through the guided modes of the PhC and found that in contrast to free-space realizations, very large topological bandgaps and the existence of an almost completely flat topological band could be realized in this setup, in which the required lattice spacing of the emitters is comparable to the optical wavelength, as demonstrated in Fig. 23(c). However, the above works simplify the atom–photon interaction Hamiltonian by tracing out the photon degrees of freedom and applying the Markov approximation, which is not valid when the electromagnetic environment has narrow bandwidth features and is highly dispersive. The Markov approximation is also violated when the length of a spontaneously emitted photon becomes comparable to or smaller than the atom spacing, which might occur for stronger atom–photon coupling, resulting in faster decay rates. Moreover, another almost universal approximation in these models is the electric dipole approximation based on the assumption that the photo wavelength is much longer than the atomic size, which may not hold for SPPs with wavelengths far smaller than free-space wavelengths. To overcome these difficulties and achieve unidirectional emission and nonreciprocal transmission of single photons, the authors of Ref. [312] studied the polaritonic band structure of 2D atomic lattices coupled to a single excitation of an SPP mode using a method that does not suffer from the limitations of Markov or dipole approximations and demonstrated that the setup allows the realization of topological gaps with arbitrary Chern numbers by manipulating the internal degree of freedom (angular momentum quantum number) of the atoms.
Quantum emitters can also interact with the bulk region of the photonic lattice rather than its edge, and this was studied in Ref. [313], where the authors studied light–emitter interactions in 2D photonic systems in the presence of a spatially homogeneous synthetic magnetic field for light and found for increasing magnetic field, the photonic modes change from extended plane waves to circulating Landau levels, leading to the formation of strongly coupled Landau-photon polaritons. This phenomenon could be understood from the fact that an emitted photon cannot propagate away, but it is constrained to orbit around the emitter due to the effective Lorentz force. Moreover, by being composed of circulating and dispersionless, but still spatially extended, photons, the spectral and dynamical features of these quasiparticles can be continuously tuned from a single-mode, cavity quantum electrodynamics (QED) type behavior to that of a many-body system of strongly interacting particles in the presence of a magnetic field.
Topological photonic modes can also mediate exotic interaction between quantum emitters when they interact with such photonic baths, e.g., Dirac photonics have been the possibility of obtaining decoherence-free, power-law interactions between emitters when many of them couple to these types of structures. In Ref. [314], the authors developed a semianalytical theory of dipole radiation near photonic Dirac points in realistic structures, which allows the authors to compute the effective photon mediated interactions along the whole unit cell. Using this theory, the authors found positions where the nature of the collective interactions changes from being coherent to dissipative ones, which might lead to strong super/subradiant effects. Finally, cavity-embedded metasurfaces [311,315,316] have also been proposed to tailor the topological properties of regular arrays of quantum emitters.
For example, in Ref. [311], the authors showed that rather than tuning the lattice structure of an emitter array, manipulating the surrounding photonic environment can also be used to tune the topological properties of the system. As shown in Fig. 23(d), the authors considered a honeycomb array of quantum emitters supporting two distinct species of massless Dirac polaritons, namely, type I and type II, and demonstrated that modifying only the photonic environment via an enclosing cavity allows one to manipulate the location of type-II Dirac points, leading to qualitatively different polariton phases. This novel feature enables one to alter the fundamental properties of the emergent Dirac polaritons while preserving the lattice structure—a unique scenario that has no analog in real or artificial graphene systems. Applying this method to a strained honeycomb metasurface that creates pseudo-magnetic fields [315], the authors demonstrated that the pseudo-magnetic field can be tuned by modifying the surrounding electromagnetic environment via enclosing the metasurface array of quantum emitters in a cavity waveguide, without altering the strain configuration. This method can also induce topological transition in arrays of quantum emitters coupled to a cavity waveguide as demonstrated in Ref. [316], where the authors considered a kagomé metasurface of quantum emitters embedded in a cavity waveguide and showed that varying the cavity width modifies the nature of the dipole–dipole interactions, which enables one to manipulate the Berry curvature and invert the valley-Chern numbers without inverting the symmetry-breaking perturbation, i.e., one can switch the chirality of the polariton valley-Hall edge states entirely by changing only the local photonic environment.
5. CONCLUSION AND PERSPECTIVE
In this review, we have introduced the recent developments of TM from passive to active, then to quantum. First, passive TMs based on different physics and phenomena are surveyed. To realize the analog QH TM, an external magnetic field is needed to break the TR symmetry. TR preserving TM without the need of magnetic fields could also be realized, e.g., the analog QSH TM, QVH TM, and Floquet TM. While the above phenomena are mostly based on the bulk-edge correspondence principle, other TMs, such as based on BICs and skyrmions, have also been studied. Different from passive TMs that mainly focus on a static or predefined functionality, active TMs can have many advantages in practice, and as examples, we have discussed nonlinear TMs and reconfigurable TMs. For nonlinear TMs, we have discussed nonlinear frequency conversion as well as topological lasers. For reconfigurable TMs, different ways to realize the reconfigurability, such as electrical, optical, mechanical, and thermal, have been examined. Finally, we have discussed how TMs can advance the study of quantum optics, e.g., TM can not only protect single or multi-photon states, but also integrate with quantum emitters to create strongly interacting topological quantum metasurfaces.
The research of TMs is a fast-evolving area, and before we end this review, we highlight some current challenges and future directions. Regarding passive TMs, the topological properties of analog QH TMs are the most robust ones due to the fact that applied external magnetic fields break the TR symmetry and remove the backscattering channels completely. Currently, analog QH TMs are most realized in the microwave regimes due to the weak magnetic-optical responses at higher frequencies. It remains to be seen whether materials with strong magnetic-optical responses could be synthesized at optical frequencies, which would open a new chapter for possible applications of analog QH TMs.
On the other hand, though analog QSH TMs and analog QVH TMs can be realized in all-dielectric materials without magnetic fields, the robustness of the corresponding topological edge states is diminished. Moreover, the current studies of analog QVH TMs are mostly based on a hexagonal lattice symmetry where Dirac cones and thus the valleys are pinned at points of the BZ. It would be interesting to explore scenarios where the positions of valleys could be tuned freely in the BZ and to study the robustness of the resulting valley edge states when the positions of the valleys are tuned.
Regarding Floquet TMs, though both dynamic and effective modulations have been proposed to realize Floquet TM in the literature, to date, those based on dynamic modulations have not been experimentally demonstrated, due to the extremely weak electro-optical effects and nonlinearity of materials, especially at high frequencies. On the other hand, the effective modulations have been experimentally demonstrated; however, they are so far limited in a coupled ring resonator scheme. In the future, more effort will be needed on advanced experimental technologies for dynamically modulated TMs and effective-modulation schemes beyond coupled ring-resonators array.
For high-order TMs, currently, most of the topological corner states are realized via the nontrivial bulk dipole moment, and the original pi-flux model for realizing topological corner states based on nontrivial bulk quadrupole moments is not very convenient for optical metasurfaces, as one would need to find a way to implement negative coupling in the pi-flux model. In the future, proposing new models without negative coupling that host nontrivial bulk quadrupole moments and could be implemented using all-dielectric materials for optical metasurfaces, would be interesting for high-order TMs.
For TMs based on BICs and skyrmions, the super-high Q factors possessed by BICs can be used to remove radiation loss during light propagation, enhance nonlinear conversion efficiency, and improve the sensitivity of sensors. BICs also introduce new possibilities for lasers and give rise to highly directional lasers, vortex lasers, and lasers exhibiting ultrafast all-optical switching. Optical skyrmion-related concepts could open a new avenue for topological photonics and can lead to new possibilities in light manipulations, e.g., polarization skyrmions offer the freedom to generate almost any polarization of light within a narrow physical space. Besides continuous waves, skyrmion-related concepts can also be generalized to space–time wave packets, which can propagate nondispersively in free space or even dispersive media and thus play the role of information carriers in communications with light. Moreover, it is worth to notice that an electrical circuit is another important platform to study exotic topological physics, leading to the emergence of topological circuits [317–322]. Due to high degrees of freedom and convenient experimental implementations, a topological circuit is a promising platform to study active and nonlinear topological systems as well as high-dimensional and non-abelian topological insulators.
Active TM has promising applications in the development of advanced photoelectric devices. However, to further facilitate the applications of active TMs, there are several challenges deserving to be addressed. In nonlinear TMs, high-power stimulation and low conversion efficiency are still two primary bottlenecks in the development of low-power and high-performance nonlinear devices in practical applications. In reconfigurable metasurfaces, it is very important to develop compact, intelligent, ultrafast controllable systems. For instance, recent studies have proposed some compact reconfigurable TMs based on CMOS integrated technology. However, the integration of TM with its external control part is still a challenge. Moreover, we can now precisely control each unit cell of TMs. But, with the increment of unit cells, it would be able and worthy to develop a smart approach to design intelligent TMs for the implementation of more sophisticated functionalities.
Finally, harnessing the power of TMs for future quantum technological applications is very promising, as topological features of metasurfaces can effectively protect the fragility of quantum states. While TMs coupled with a few quantum emitters have been demonstrated in experiments, the coupling of TM with a regular array of quantum emitters has not been demonstrated, and the realization of such strongly interacting topological quantum metasurfaces would allow the exploration of many interesting problems, from topological quantum computing to strongly interacting topological phases of light. We believe TMs will continue to be an active and exciting area of research in the years to come in terms of both fundamental research and practical applications.
References
[32] M. Kim, J. Rho. Quantum Hall phase and chiral edge states simulated by a coupled dipole method. Phys. Rev. B, 101, 195105(2020).
[80] J. W. Liu, F. L. Shi, X. T. He, G. J. Tang, W. J. Chen, X. D. Chen, J. W. Dong. Valley photonic crystals. Adv. Phys. X, 6, 1905546(2021).
[92] S. Yin, E. Galiffi, A. Alù. Floquet metamaterials. eLight, 2, 8(2022).
[109] M. Miri, A. Alù. Exceptional points in optics and photonics. Science, 363, r7709(2019).
[135] J. V. Neumann, E. Wigner. Über merkwürdige diskrete eigenwerte. Phys. Z., 30, 465-467(1929).
[167] T. H. Skyrme. A non-linear field theory. Proc. R. Soc. London Ser. A, 260, 127-138(1961).
[168] T. H. R. Skyrme. A unified field theory of mesons and baryons. Nucl. Phys., 31, 556-569(1962).
[169] I. Zahed, G. E. Brown. The Skyrme model. Phys. Rep., 142, 1-102(1986).
[172] Y. Tokura, N. Kanazawa. Magnetic skyrmion materials. Chem. Rev., 121, 2857-2897(2021).
[174] X. Zhang, Y. Zhou, K. M. Song, T.-E. Park, J. Xia, M. Ezawa, X. Liu, W. Zhao, G. Zhao, S. Woo. Skyrmion-electronics: writing, deleting, reading and processing magnetic skyrmions toward spintronic applications. J. Phys. Condens. Matter, 32, 143001(2020).
[198] A. Karnieli, A. Arie. All-optical Stern-Gerlach effect. Phys. Rev. Lett., 120, 053901(2018).
[200] G. Chen. Skyrmion Hall effect. Nat. Phys., 13, 112-113(2017).
[319] S. Liu, W. Gao, Q. Zhang, S. Ma, L. Zhang, C. Liu, Y. J. Xiang, T. J. Cui, S. Zhang. Topologically protected edge state in two-dimensional Su–Schrieffer–Heeger circuit. Research, 2019, 8609875(2019).

Set citation alerts for the article
Please enter your email address



