Abstract
The recent emerging field of synthetic dimension in photonics offers a variety of opportunities for manipulating different internal degrees of freedom of photons such as the spectrum of light. While nonlinear optical effects can be incorporated into these photonic systems with synthetic dimensions, these nonlinear effects typically result in long-range interactions along the frequency axis. Thus, it has been difficult to use the synthetic dimension concept to study a large class of Hamiltonians that involves local interactions. Here we show that a Hamiltonian that is locally interacting along the synthetic dimension can be achieved in a dynamically modulated ring resonator incorporating nonlinearity, provided that the group velocity dispersion of the waveguide forming the ring is specifically designed. As a demonstration we numerically implement a Bose–Hubbard model and explore photon blockade effect in the synthetic frequency space. Our work opens new possibilities for studying fundamental many-body physics in the synthetic space in photonics, with potential applications in optical quantum communication and quantum computation.1. INTRODUCTION
The concept of the synthetic dimension enables one to explore higher-dimensional physics in lower-dimensional systems [1–14]. In photonics [15,16], the synthetic dimension can be achieved by exploiting various degrees of freedom of light such as its frequency [17,18], spatial mode [19], or orbital angular momentum [20], and by specifically controlling the coupling between these degrees of freedom [21–23]. While initially explored mostly theoretically [24–30], very recently there have been a number of important experimental developments, including the first experimental demonstration of topological insulators with synthetic dimensions [19], the observation of the effective gauge potential in two independent synthetic dimensions [31], the measurement of band structure along the frequency axis of light [32], and the control of the light spectrum in synthetic space [33,34].
Most of the existing theoretical and experimental works on the synthetic dimension in photonics concern linear processes without photon-photon interactions. Certainly, it would be of interest to consider nonlinear systems where there is photon-photon interaction. Moreover, since one of the major objectives by going into synthetic dimension is to create a platform to study specific interacting Hamiltonians that are of physical significance, it would be important to develop a strategy to synthesize these interacting Hamiltonians. A very large class of interesting interacting Hamiltonians have local interactions [35–39]. For example, in the Bose–Hubbard Hamiltonian where () are the creation (annihilation) operators for photons on the th lattice site, is the coupling coefficient, and is the local nonlinear strength. The interaction term consists only of on-site interaction. Attempts to achieve such locally interacting Hamiltonians in synthetic space have been made in photonics in the geometric angular coordinate [40] and also in ultracold atoms with spin being the internal degree of freedom [41]. On the other hand, as is known and we will briefly reiterate below, the standard form of nonlinear optics typically leads to a form of interaction that is nonlocal in the synthetic space [42,43], i.e., the Hamiltonian contains terms such as , which describe interactions of photons at different lattice sites. How to achieve a Hamiltonian where the interactions are completely local in the synthetic space for photons thus represents an important open theoretical question.
In this paper, we consider a synthetic frequency dimension of light, formed in a ring resonator incorporating a modulator. To create photon-photon interaction we consider processes in the waveguide forming the ring. We show that a local photon-photon interaction in the frequency dimension can be achieved with a careful design of the group velocity dispersion of the waveguide [Fig. 1(a)]. As a demonstration we show that this system can be used to demonstrate a Bose–Hubbard model and achieve photon-blockade effects along the synthetic axis. This work here significantly broadens the range of physics phenomena that can be studied in photonic synthetic space and may lead to new opportunities in quantum simulations and in the manipulation of light.
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
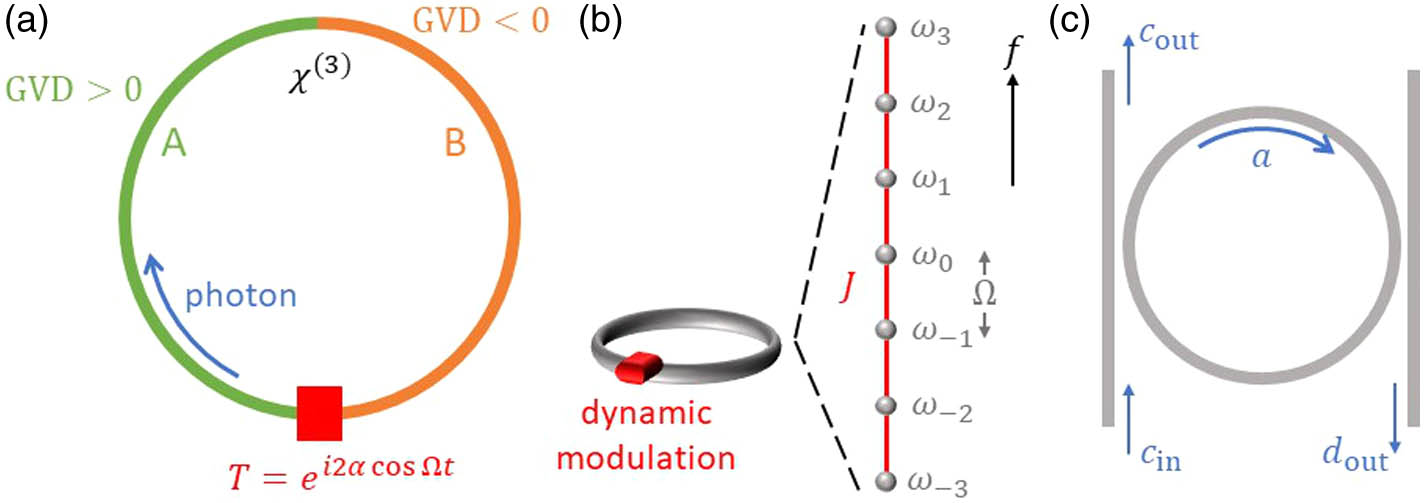
Figure 1.(a) A ring resonator, composed by two types of single-mode waveguides A and B, undergoing the dynamic modulation. (b) A ring under the dynamic modulation supports a synthetic lattice along the frequency dimension. (c) The ring is coupled with the through-port and drop-port waveguides.
2. MODEL
We start with a brief review of the ring resonator under the dynamic modulation as shown in Fig. 1(b) [24,44], which naturally leads to a synthetic dimension of light along the frequency axis. We consider a ring composed by a single-mode waveguide with an effective refractive index and a length . For simplicity, assuming zero group velocity dispersion in the waveguide, the ring resonator supports resonant modes at the resonant frequencies , where is the free spectral range (FSR) for the ring. We place a phase modulator inside the ring and choose the modulation frequency to be equal to the FSR. The transmission of light passing through the modulator can be described by a time-dependent transmission coefficient [45] where is the modulation amplitude. We assume that the field experiences small changes for each round-trip. Then, after one round-trip, the change of the field amplitude for the th resonant mode can be written as [24] where is the slow time variable [46]. Equation (3) is valid when , so one can safely neglect the generation of sidebands with orders larger than 1 for light passing through the modulator. The dynamics of Eq. (3) is described by an effective Hamiltonian:
Here is the modulation strength and () is the annihilation (creation) operator for the th resonant mode. The Hamiltonian in Eq. (4) describes a one-dimensional tight-binding model along the synthetic frequency axis [see Fig. 1(b)]. With this approach, a wide variety of noninteracting Hamiltonians with different connectivities and topological properties can be created [15]. However, there have been far less works on creating important interacting Hamiltonians.
As an illustration of the general difficulty as well as our approach of creating locally interacting Hamiltonians in the frequency synthetic dimension, we aim to synthesize the effective Bose–Hubbard Hamiltonian in Eq. (1) in the synthetic frequency dimension. Although nonlinear optical phenomena in many photonic materials have been extensively studied, creating the Hamiltonian of Eq. (1) in the frequency synthetic space is in fact nontrivial [42]. The introduction of the nonlinearity typically leads to long-range interactions over all synthetic lattice sites. For example, the dynamically modulated ring as shown in Fig. 1(b), with a third-order nonlinear susceptibility , is described by an interacting Hamiltonian [43] as can be derived using the rotating wave approximation. In Eq. (5), the second and third terms describe two four-wave-mixing (FWM) effects. The second term describes the hyperparametric oscillation process involving four modes with frequency relationship . The third term describes the third-harmonic generation (THG) process with . Comparing Eq. (1) with Eq. (5), we see that the interacting term in Eq. (1) corresponds to the self-phase modulation (SPM) process. In Eq. (5), however, in addition to the SPM process, other terms that describe the cross-phase modulation (XPM) process, other hyperparametric processes, and the THG process result in long-range interactions between different resonant modes in the ring (see Fig. 2). While here for illustration purposes we consider a specific type of nonlinearity, the observation is in fact rather general: standard nonlinearity does not lead to local interactions in the synthetic frequency dimension.

Figure 2.Four-wave-mixing processes in a ring with a third-order nonlinear susceptibility including the hyper-parametric processes (SPM, XPM, and others) and the THG process.
In order to synthesize the Bose–Hubbard model where the interaction is local along the frequency dimension, we propose a ring consisting of two sections of waveguides. The two sections have the same nonlinear susceptibility. However, they have opposite GVD as illustrated in Fig. 1(a). In the linear regime of light propagation, for each complete round-trip as light goes around the ring, the dispersion effect in the two waveguide sections cancels. Hence, this ring also features equally spaced resonances along the frequency axis, same as a ring with zero GVD, and a one-dimensional synthetic frequency dimension can be created in this ring by applying the dynamic modulation. On the other hand, in each waveguide section, due to the GVD, the only phase-matched processes are the SPM and XPM processes. Moreover, as we will show below, in any Hilbert space with a fixed photon number, the Hamiltonian including both SPM and XPM processes in fact reduces to a Hamiltonian only including the SPM process. We therefore show that our design supports an effective Bose–Hubbard Hamiltonian [Eq. (1)] along the frequency axis.
In the following, we explain our design in detail: we start with reviewing the light propagating in a dispersive waveguide, followed by considering the FWM process in such a waveguide, and then go to the discussion of the ring composed of dispersive waveguides with nonlinearity. We first consider light propagating inside a single-mode waveguide. The evolution of the field amplitude with the frequency at the position in the waveguide can be described as [47] where denotes the propagation wavevector. can be expanded around the reference frequency , i.e., Here we set , is the group velocity, and is the GVD around . By neglecting the higher-order terms in Eq. (7), one can write the field amplitude of light after it propagates through a waveguide with the length : Note that the GVD induces a frequency-dependent phasedelay.
Next, we explore the light propagating through the waveguide section having a positive GVD () and as shown in Fig. 1(a). For simplicity, we consider two incident waves with the frequencies and in the vicinity of the reference frequency . We look for the solution for a general FWM process where output fields are generated at frequencies and , satisfying the energy conservation relation [see Fig. 3(a)]. We also assume the narrowband limit, i.e., , . The resulting coupled-mode equations under the slowly varying amplitude approximation are [42] where and the momentum mismatch is At frequencies around , the phase-matching condition () is satisfied if , which corresponds to the SPM process, or and , which correspond to the XPM process. For other FWM processes with the phase-mismatching condition , the efficiency for frequency conversion is proportional to the phase-mismatch factor, i.e., , as plotted in Fig. 3(b). For , the conversion efficiency is significantly suppressed. In particular, for with being the positive integer, , meaning that FWM processes other than SPM and XPM vanish completely. A similar argument is also valid for the THG process, where the conversion efficiency of THG is also strongly reduced due to the phase mismatching.

Figure 3.(a) A general four-wave-mixing process in a waveguide with the third-order susceptibility . (b) The plot of showing the effect of the phase mismatching.
Having treated a light propagation effect in a single waveguide section, we now discuss the ring in Fig. 1(a). The waveguide A with the length has a positive GVD (). The waveguide B with the length has a negative GVD (), and we assume that . The quadratic term of the phase delay in Eq. (8) due to the dispersion effect is therefore compensated once the light propagates through the entire ring. Hence, this ring supports equally spaced resonant modes at the resonant frequencies with the FSR . As light goes through each round-trip, its amplitude experiences a small change due to both the nonlinearity and the dynamic modulation. After a round-trip, the change of the field amplitude for the th mode at frequency can be written from Eqs. (3), (9), and (10): where is the slow time variable. The corresponding effective Hamiltonian from Eq. (12) reads Here describes the strength of the nonlinearity [48,49], where is the effective mode volume, , and is the permittivity of free space.
In a Hilbert space where the total number of photons is conserved in the system, Eq. (13) can be further simplified by noting that The resulting Hamiltonian reads One notices that the third term is just a constant shift in energy. The change of sign in the second term does not affect the physical observables for bosonic systems. Hence, the Hamiltonian Eq. (15) [or the Hamiltonian Eq. (13)] describes the same physics as our desired Hamiltonian in Eq. (1). We have therefore shown that a Bose–Hubbard model [50–52] with local interaction in the synthetic frequency dimension can be achieved by the ring shown in Fig. 1(a).
3. RESULTS AND DISCUSSIONS
To demonstrate some of the physics effects along the synthetic frequency dimension in the Hamiltonian Eq. (13), we perform numerical simulations with photon number . External waveguides are coupled with the ring, where the photons are input into the ring from the through-port and the detection can be made at the drop-port waveguide [see Fig. 1(c)]. Hence, our system becomes open, and the photon transport property is described by the input-output formalism in the Heisenberg picture [53,54]: where is the waveguide-cavity coupling strength. () and are the input (out) annihilation operators for photons at the frequency in the through-port and drop-port waveguides, respectively.
As the input state, we consider a strongly correlated photon pair [55] which satisfies the normalization condition . We further assume that has an extremely short temporal width. Hence, the input state Eq. (19) describes the scenario where two photons at the frequencies and are simultaneously injected into the through-port waveguide. We choose , where describes the timing of the incident photons, is the pulse temporal width, and is the small frequency detuning. To excite the individual sites in the synthetic lattice along the frequency dimension, the condition is required.
To measure the quantum statistics of the photons inside the ring, we define the two-photon correlation function [56]. We then compute the two-photon correlation probability in which two output photons coincide in time
The simulation procedure follows the standard formalism [55] but in the synthetic frequency dimension. We consider the synthetic lattice in Fig. 1(b) involving 31 resonant modes () and set , , and . We also choose to compensate for the overall frequency shift in the effective Bose–Hubbard model. A photon pair is injected into the waveguide. We consider the cases with , , and in the simulations. Normalized distributions of the two-photon correlation probability for each choice of are plotted in Figs. 4(a)–4(c). There is no photon interaction in the case. Notice the existence of nonzero probability , where the output photons have the same frequency. As the interaction increases, the output photon statistics changes. For a large , the correlation probability for all . High nonlinearity thus introduces a large blockade effect at each resonant mode along the synthetic frequency dimension.

Figure 4.Normalized distributions of the two-photon correlation probability . (a)–(c) The input photon pair is with , , and , respectively. (d)–(f) The input photon pair is with , , and , respectively. Positions inside two dashed lines correspond to .
We next use the photon pair as the input and assume that there is a sharp boundary at in the synthetic frequency dimension. Such an artificial sharp boundary can be created by adding another ring to strongly couple only to the th resonant mode but no other modes [30]. In this input state the two photons have the same carrier frequencies. Figures 4(d)–4(f) show the simulated normalized distributions of the two-photon correlation probability for different . At , there is a strong probability for the two photons to have the same frequencies. In contrast, with a large nonlinearity , away from the input frequency at , there is very little probability that the output photons exhibit the same frequencies. Again, we see a strong photon-blockade effect in the synthetic frequency dimension.
Simulations in Fig. 4 show the photon-photon interaction along the synthetic frequency dimension, which is an analog to the on-site nonlinear interaction in the spatial dimension [57–59]. Moreover, we note that simulation results in Fig. 4 are the same as results performed by simulating Eqs. (16)–(18) with replaced by in Eq. (1), indicating that the Hamiltonian in Eq. (13) indeed provides an implementation of the Bose–Hubbard model in the synthetic frequency dimension.
Our proposed system requires waveguides with strong nonlinearity and large GVD, which is experimentally challenging but may be achievable with the current state-of-the-art technology. For a ring with the length , is . The modulation strength can be tuned at the order of 0.1–1 GHz to make the system operate in the weak modulation regime. As an example, photonic crystal fiber filled with a high-density atomic gas has the potential to create a nonlinearity with up to in the few-photon regime [60]. Moreover, the strong nonlinearity in optical resonators is potentially feasible with other nanophotonic systems [36,61–66], for example, nanophotonic waveguides incorporated with rubidium vapors [67–69]. Strong GVD is desired to bring the phase-mismatching condition , which can be simplified to . The necessary high dispersion is possible with dispersion engineering in the photonic crystal fiber [70] or by exploiting mode crossing in coupled waveguides [71]. The theoretical proposal here may also be implementable in the microwave frequency range using superconducting quantum circuits [72].
4. CONCLUSION
In summary, we show that a ring resonator undergoing dynamic modulation can be used to achieve an interacting Hamiltonian where the interaction is local along the synthetic frequency dimension, provided that the ring incorporates nonlinearity, and with a specific design of the GVD of the ring. Our work complements other emerging efforts in creating locally interacting Hamiltonians in synthetic space, by showing that such locally interacting Hamiltonians can be achieved in a system that has been widely used in photonics. The possibility of creating locally interacting Hamiltonians in the synthetic frequency dimension is fundamentally important for future studies of photon-photon interactions and many-body physics with synthetic dimensions in photonics, with promising potentials for a variety of quantum optical applications such as quantum information science and quantum communication technology [35,73].
We noticed Ref. [41] when we were in the final stage of preparing this paper.
References
[1] O. Boada, A. Celi, J. I. Latorre, M. Lewenstein. Quantum simulation of an extra dimension. Phys. Rev. Lett., 108, 133001(2012).
[2] D. Jukić, H. Buljan. Four-dimensional photonic lattices and discrete tesseract solitons. Phys. Rev. A, 87, 013814(2013).
[3] A. Celi, P. Massignan, J. Ruseckas, N. Goldman, I. B. Spielman, G. Juzeliūnas, M. Lewenstein. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett., 112, 043001(2014).
[4] M. Mancini, G. Pagano, G. Cappellini, L. Livi, M. Rider, J. Catani, C. Sias, P. Zoller, M. Inguscio, M. Dalmonte, L. Fallani. Observation of chiral edge states with neutral fermions in synthetic Hall ribbons. Science, 349, 1510-1513(2015).
[5] B. K. Stuhl, H.-I. Lu, L. M. Aycock, D. Genkina, I. B. Spielman. Visualizing edge states with an atomic Bose gas in the quantum Hall regime. Science, 349, 1514-1518(2015).
[6] B. Gadway. Atom-optics approach to studying transport phenomena. Phys. Rev. A, 92, 043606(2015).
[7] D.-W. Wang, R.-B. Liu, S.-Y. Zhu, M. O. Scully. Superradiance lattice. Phys. Rev. Lett., 114, 043602(2015).
[8] L. F. Livi, G. Cappellini, M. Diem, L. Franchi, C. Clivati, M. Frittelli, F. Levi, D. Calonico, J. Catani, M. Inguscio, L. Fallani. Synthetic dimensions and spin-orbit coupling with an optical clock transition. Phys. Rev. Lett., 117, 220401(2016).
[9] S. Kolkowitz, S. L. Bromley, T. Bothwell, M. L. Wall, G. E. Marti, A. P. Koller, X. Zhang, A. M. Rey, J. Ye. Spin-Corbit-coupled fermions in an optical lattice clock. Nature, 542, 66-70(2017).
[10] H. M. Price, T. Ozawa, N. Goldman. Synthetic dimensions for cold atoms from shaking a harmonic trap. Phys. Rev. A, 95, 023607(2017).
[11] I. Martin, G. Refael, B. Halperin. Topological frequency conversion in strongly driven quantum systems. Phys. Rev. X, 7, 041008(2017).
[12] Y. Baum, G. Refael. Setting boundaries with memory: generation of topological boundary states in Floquet-induced synthetic crystals. Phys. Rev. Lett., 120, 106402(2018).
[13] H. Cai, J. Liu, J. Wu, Y. He, S.-Y. Zhu, J.-X. Zhang, D.-W. Wang. Experimental observation of momentum-space chiral edge currents in room-temperature atoms. Phys. Rev. Lett., 122, 023601(2019).
[14] K. Tschernig, R. J. de León-Montiel, A. Pérez-Leija, K. Busch. Multiphoton synthetic lattices in multiport waveguide arrays: synthetic atoms and Fock graphs. Photon. Res., 8, 1161-1170(2020).
[15] L. Yuan, Q. Lin, M. Xiao, S. Fan. Synthetic dimension in photonics. Optica, 5, 1396-1405(2018).
[16] T. Ozawa, H. M. Price. Topological quantum matter in synthetic dimensions. Nat. Rev. Phys., 1, 349-357(2019).
[17] L. Yuan, Y. Shi, S. Fan. Photonic gauge potential in a system with a synthetic frequency dimension. Opt. Lett., 41, 741-744(2016).
[18] T. Ozawa, H. M. Price, N. Goldman, O. Zilberberg, I. Carusotto. Synthetic dimensions in integrated photonics: from optical isolation to four-dimensional quantum Hall physics. Phys. Rev. A, 93, 043827(2016).
[19] E. Lustig, S. Weimann, Y. Plotnik, Y. Lumer, M. A. Bandres, A. Szameit, M. Segev. Photonic topological insulator in synthetic dimensions. Nature, 567, 356-360(2019).
[20] X.-W. Luo, X. Zhou, C.-F. Li, J.-S. Xu, G.-C. Guo, Z.-W. Zhou. Quantum simulation of 2D topological physics in a 1D array of optical cavities. Nat. Commun., 6, 7704(2015).
[21] A. Schwartz, B. Fischer. Laser mode hyper-combs. Opt. Express, 21, 6196-6204(2013).
[22] L. Yuan, M. Xiao, Q. Lin, S. Fan. Synthetic space with arbitrary dimensions in a few rings undergoing dynamic modulation. Phys. Rev. B, 97, 104105(2018).
[23] E. Lustig, Y. Plotnik, Z. Yang, M. Segev. 3D parity time symmetry in 2D photonic lattices utilizing artificial gauge fields in synthetic dimensions. Conference on Lasers and Electro-Optics, FTu4B.1(2019).
[24] L. Yuan, S. Fan. Bloch oscillation and unidirectional translation of frequency in a dynamically modulated ring resonator. Optica, 3, 1014-1018(2016).
[25] Q. Lin, M. Xiao, L. Yuan, S. Fan. Photonic Weyl point in a two-dimensional resonator lattice with a synthetic frequency dimension. Nat. Commun., 7, 13731(2016).
[26] Y. Zhang, Y. Zhu. Generation of Weyl points in coupled optical microdisk-resonator arrays via external modulation. Phys. Rev. A, 96, 013811(2017).
[27] X.-W. Luo, X. Zhou, J.-S. Xu, C.-F. Li, G.-C. Guo, C. Zhang, Z.-W. Zhou. Synthetic-lattice enabled all-optical devices based on orbital angular momentum of light. Nat. Commun., 8, 16097(2017).
[28] X.-F. Zhou, X.-W. Luo, S. Wang, G.-C. Guo, X. Zhou, H. Pu, Z.-W. Zhou. Dynamically manipulating topological physics and edge modes in a single degenerate optical cavity. Phys. Rev. Lett., 118, 083603(2017).
[29] X.-W. Luo, C. Zhang, G.-C. Guo, Z.-W. Zhou. Topological photonic orbital-angular-momentum switch. Phys. Rev. A, 97, 043841(2018).
[30] L. Yuan, Q. Lin, A. Zhang, M. Xiao, X. Chen, S. Fan. Photonic gauge potential in one cavity with synthetic frequency and orbital angular momentum dimensions. Phys. Rev. Lett., 122, 083903(2019).
[31] A. Dutt, Q. Lin, L. Yuan, M. Minkov, M. Xiao, S. Fan. A single photonic cavity with two independent physical synthetic dimensions. Science, 367, 59-64(2020).
[32] A. Dutt, M. Monkov, Q. Lin, L. Yuan, D. A. B. Miller, S. Fan. Experimental band structure spectroscopy along a synthetic dimension. Nat. Commun., 10, 3122(2019).
[33] B. A. Bell, K. Wang, A. S. Solntsev, D. N. Neshev, A. A. Sukhorukov, B. J. Eggleton. Spectral photonic lattices with complex long-range coupling. Optica, 4, 1433-1436(2017).
[34] C. Qin, F. Zhou, Y. Peng, D. Sounas, X. Zhu, B. Wang, J. Dong, X. Zhang, A. Alù, P. Lu. Spectrum control through discrete frequency diffraction in the presence of photonic gauge potentials. Phys. Rev. Lett., 120, 133901(2018).
[35] I. Bloch, J. Dalibard, W. Zwerger. Many-body physics with ultracold gases. Rev. Mod. Phys., 80, 885-964(2008).
[36] D. E. Chang, V. Vuletić, M. D. Lukin. Quantum nonlinear optics–photon by photon. Nat. Photonics, 8, 685-694(2014).
[37] M. E. Tai, A. Lukin, M. Rispoli, R. Schittko, T. Menke, D. Borgnia, P. M. Preiss, F. Grusdt, A. M. Kaufman, M. Greiner. Microscopy of the interacting Harper-CHofstadter model in the two-body limit. Nature, 546, 519-523(2017).
[38] D. Roy, C. M. Wilson, O. Firstenberg. Colloquium: strongly interacting photons in one-dimensional continuum. Rev. Mod. Phys., 89, 021001(2017).
[39] D. A. Abanin, E. Altman, I. Bloch, M. Serbyn. Colloquium: many-body localization, thermalization, and entanglement. Rev. Mod. Phys., 91, 021001(2019).
[40] T. Ozawa, I. Carusotto. Synthetic dimensions with magnetic fields and local interactions in photonic lattices. Phys. Rev. Lett., 118, 013601(2017).
[41] L. Barbiero, L. Chomaz, S. Nascimbene, N. Goldman. Bose-Hubbard physics in synthetic dimensions from interaction trotterization(2019).
[42] R. W. Boyd. Nonlinear Optics(2008).
[43] D. V. Strekalov, C. Marquardt, A. B. Matsko, H. G. L. Schwefel, G. Leuchs. Nonlinear and quantum optics with whispering gallery resonators. J. Opt., 18, 123002(2016).
[44] H. Sambe. Steady states and quasienergies of a quantum-mechanical system in an oscillating field. Phys. Rev. A, 7, 2203-2213(1973).
[45] A. Yariv, P. Yeh. Photonics: Optical Electronics in Modern Communications(2007).
[46] H. A. Haus. Mode-locking of lasers. IEEE J. Sel. Top. Quantum Electron., 6, 1173-1185(2000).
[47] H. A. Haus. Waves and Fields in Optoelectronics(1984).
[48] A. B. Matsko, A. A. Savchenkov, D. Strekalov, V. S. Ilchenko, L. Maleki. Optical hyperparametric oscillations in a whispering-gallery-mode resonator: threshold and phase diffusion. Phys. Rev. A, 71, 033804(2005).
[49] Y. K. Chembo, D. V. Strekalov, N. Yu. Spectrum and dynamics of optical frequency combs generated with monolithic whispering gallery mode resonators. Phys. Rev. Lett., 104, 103902(2010).
[50] M. Hafezi, D. E. Chang, V. Gritsev, E. Demler, M. D. Lukin. Quantum transport of strongly interacting photons in a one-dimensional nonlinear waveguide. Phys. Rev. A, 85, 013822(2012).
[51] A. Biella, L. Mazza, I. Carusotto, D. Rossini, R. Fazio. Photon transport in a dissipative chain of nonlinear cavities. Phys. Rev. A, 91, 053815(2015).
[52] K. G. L. Pedersen, M. Pletyukhov. Few-photon scattering on Bose-Hubbard lattices. Phys. Rev. A, 96, 023815(2017).
[53] C. W. Gardiner, M. J. Collett. Input and output in damped quantum systems: quantum stochastic differential equations and the master equation. Phys. Rev. A, 31, 3761-3774(1985).
[54] S. Fan, Ş. E. Kocabaş, J.-T. Shen. Input-output formalism for few-photon transport in one-dimensional nanophotonic waveguides coupled to a qubit. Phys. Rev. A, 82, 063821(2010).
[55] L. Yuan, M. Xiao, S. Xu, S. Fan. Creating anyons from photons using a nonlinear resonator lattice subject to dynamic modulation. Phys. Rev. A, 96, 043864(2017).
[56] M. O. Scully, M. S. Zubairy. Quantum Optics(1997).
[57] K. M. Birnbaum, A. Boca, R. Miller, A. D. Boozer, T. E. Northup, H. J. Kimble. Photon blockade in an optical cavity with one trapped atom. Nature, 436, 87-90(2005).
[58] A. V. Gorshkov, J. Otterbach, M. Fleischhauer, T. Pohl, M. D. Lukin. Photon-photon interactions via Rydberg blockade. Phys. Rev. Lett., 107, 133602(2011).
[59] B. Li, R. Huang, X. Xu, A. Miranowicz, H. Jing. Nonreciprocal unconventional photon blockade in a spinning optomechanical system. Photon. Res., 7, 630-641(2019).
[60] V. Venkataraman, K. Saha, A. L. Gaeta. Phase modulation at the few-photon level for weak-nonlinearity-based quantum computing. Nat. Photonics, 7, 138-141(2013).
[61] M. Koch, C. Sames, M. Balbach, H. Chibani, A. Kubanek, K. Murr, T. Wilk, G. Rempe. Three-photon correlations in a strongly driven atom-cavity system. Phys. Rev. Lett., 107, 023601(2011).
[62] T. Volz, A. Reinhard, M. Winger, A. Badolato, K. J. Hennessy, E. L. Hu, A. Imamoğlu. Ultrafast all-optical switching by single photons. Nat. Photonics, 6, 605-609(2012).
[63] C. Junge, D. O’shea, J. Volz, A. Rauschenbeutel. Strong coupling between single atoms and nontransversal photons. Phys. Rev. Lett., 110, 213604(2013).
[64] S. Kato, T. Aoki. Strong coupling between a trapped single atom and an all-fiber cavity. Phys. Rev. Lett., 115, 093603(2015).
[65] M. Radulaski, J. L. Zhang, Y.-K. Tzeng, K. G. Lagoudakis, H. Ishiwata, C. Dory, K. A. Fischer, Y. A. Kelaita, S. Sun, P. C. Maurer, K. Alassaad, G. Ferro, Z.-X. Shen, N. A. Melosh, S. Chu, J. Vučković. Nanodiamond integration with photonic devices. Laser Photon. Rev., 13, 1800316(2019).
[66] C. K. Ha, K. S. Lee, D. Kwon, M. S. Kang. Widely tunable ultra-narrow-linewidth dissipative soliton generation at the telecom band. Photon. Res., 8, 1100-1109(2020).
[67] W. Yang, D. B. Conkey, B. Wu, D. Yin, A. R. Hawkins, H. Schmidt. Atomic spectroscopy on a chip. Nat. Photonics, 1, 331-335(2007).
[68] R. Ritter, N. Gruhler, W. Pernice, H. Kübler, T. Pfau, R. Löw. Atomic vapor spectroscopy in integrated photonic structures. Appl. Phys. Lett., 107, 041101(2015).
[69] L. Stern, B. Desiatov, N. Mazurski, U. Levy. Strong coupling and high-contrast all-optical modulation in atomic cladding waveguides. Nat. Commun., 8, 14461(2017).
[70] Y. Zhu, J. A. Greenberg, N. A. Husein, D. J. Gauthier. Giant all-optical tunable group velocity dispersion in an optical fiber. Opt. Express, 22, 14382-14391(2014).
[71] M. B. Mia, N. Jaidye, S. Kim. Extremely high dispersions in heterogeneously coupled waveguides. Opt. Express, 27, 10426-10437(2019).
[72] N. R. A. Lee, M. Pechal, E. Alex Wollack, P. Arrangoiz-Arriola, Z. Wang, A. H. Safavi-Naeini. Electric fields for light: propagation of microwave photons along a synthetic dimension(2019).
[73] T. Ozawa, H. M. Price, A. Amo, N. Goldman, M. Hafei, L. Lu, M. C. Rechtsman, D. Schuster, J. Simon, O. Zilberberg, I. Carusotto. Topological photonics. Rev. Mod. Phys., 91, 015006(2019).

![]()
![]()
![]()




