Abstract
Squeezed vacuum, as a nonclassical field, has many interesting properties and results in many potential applications for quantum measurement and information processing. Here, we investigate a single atom–cavity quantum electrodynamics (QED) system driven by a broadband squeezed vacuum. In the presence of the atom, we show that both the mean photon number and the quantum fluctuations of photons in the cavity undergo a significant depletion due to the additional transition pathways generated by the atom–cavity interaction. By measuring these features, one can detect the existence of atoms in the cavity. We also show that two-photon excitation can be significantly suppressed by the quantum destructive interference when the squeezing parameter is very small. These results presented here are helpful in understanding the quantum nature of the broadband squeezed vacuum.Cavity quantum electrodynamics (QED) is the study of the interaction between photons confined in a high-finesse cavity and quantum emitters including atoms, quantum dots, and so on, under conditions where the quantum nature of cavity photons is dominant[1,2]. The most basic model of light–matter interaction is a single atom interacting with photons in the cavity, which is known as the Jaynes–Cummings model and provides many interesting QED effects, including vacuum Rabi splitting[3], single photon blockade, and so on[4–6]. It also provides possibilities to achieve quantum information processing and communication by fully controlling the cavity QED systems[7–11].
The most essential requirement for realizing the above intriguing applications is the availability of strong coupling between the quantum emitters and cavity[2,12–14]. When a light field is confined inside the mode of a high-quality (Q) cavity, the quantum emitters, trapped inside the mode, can coherently exchange energy with the light field. As a result, the energy exchange rate becomes much larger than both the decay rate of the quantum emitters and photon decay rate from the cavity. In this case, the cavity QED system is under the condition of the so-called strong coupling[15]. Beside this, how to efficiently manipulate the quantum emitter is another key factor for realizing quantum information processing[16–24].
Due to its quantum nature and extremely high coherence, the atom is a good candidate for quantum computation and communication[25]. Benefitting from the development of laser cooling and trapping technology[26], it is possible to cool atoms from room temperature to sub-millidegrees Kelvin[27] and subsequently keep atoms trapped at single atom level for a long time. Up to now, several groups worldwide have been able to strongly couple a single or several trapped atoms to the cavity mode[28–30], which boosts the development of the cavity QED. Recently, great attention has been paid to the research of nonclassical fields due to their quantum statistical properties[31–34]. In particular, the squeezed vacuum, as a quantum state of the electromagnetic field with very special properties, has been successfully produced in laboratory[35] and widely used in artificial atom–cavity QED systems[36,37]. If the bandwidth of the squeezed vacuum is large enough, it can be treated as a reservoir to the atom subjected to such a field. However, the squeezed vacuum, contrary to the ordinary vacuum, carries some phase information, and the behavior of the atom in such a reservoir is quite different from its behavior in the ordinary vacuum. Based on these features, the squeezed vacuum has been used to detect a single atom[38] and realize the superradiant phase transition[6], multiphoton blockade[39], and so on[40–43].
Sign up for Chinese Optics Letters TOC. Get the latest issue of Chinese Optics Letters delivered right to you!Sign up now
In this Letter, we study the interaction of a single atom and the cavity driven by a broadband squeezed vacuum. Our aim is to show the features of the quantum fluctuation of the squeezed vacuum and reveal the physical mechanism of the interaction between the atom and squeezed vacuum. For an empty cavity, the broadband squeezed vacuum results in a constant mean photon number with strong quantum fluctuations at the central frequency. In the presence of the atom, additional transition pathways take place and result in energy transfer from the cavity to the atom. Therefore, significant changes of the mean photon number and the quantum fluctuations of photons in the cavity can be observed due to the interaction between the cavity and atom. By measuring these features of photons in the cavity, one can detect the existence of atoms in the cavity. We also show that additional transition pathways may result in quantum destructive interference for small squeezing parameters. Consequently, the two-photon excitation will be significantly suppressed. We note that a recent study with the same Hamiltonian reports the photon blockade phenomenon[39] by numerically solving the master equation. However, we reveal the physical mechanism of the squeezing induced blockade of the two-photon excitation, which is helpful for readers to understand the nature of the broadband squeezed vacuum.
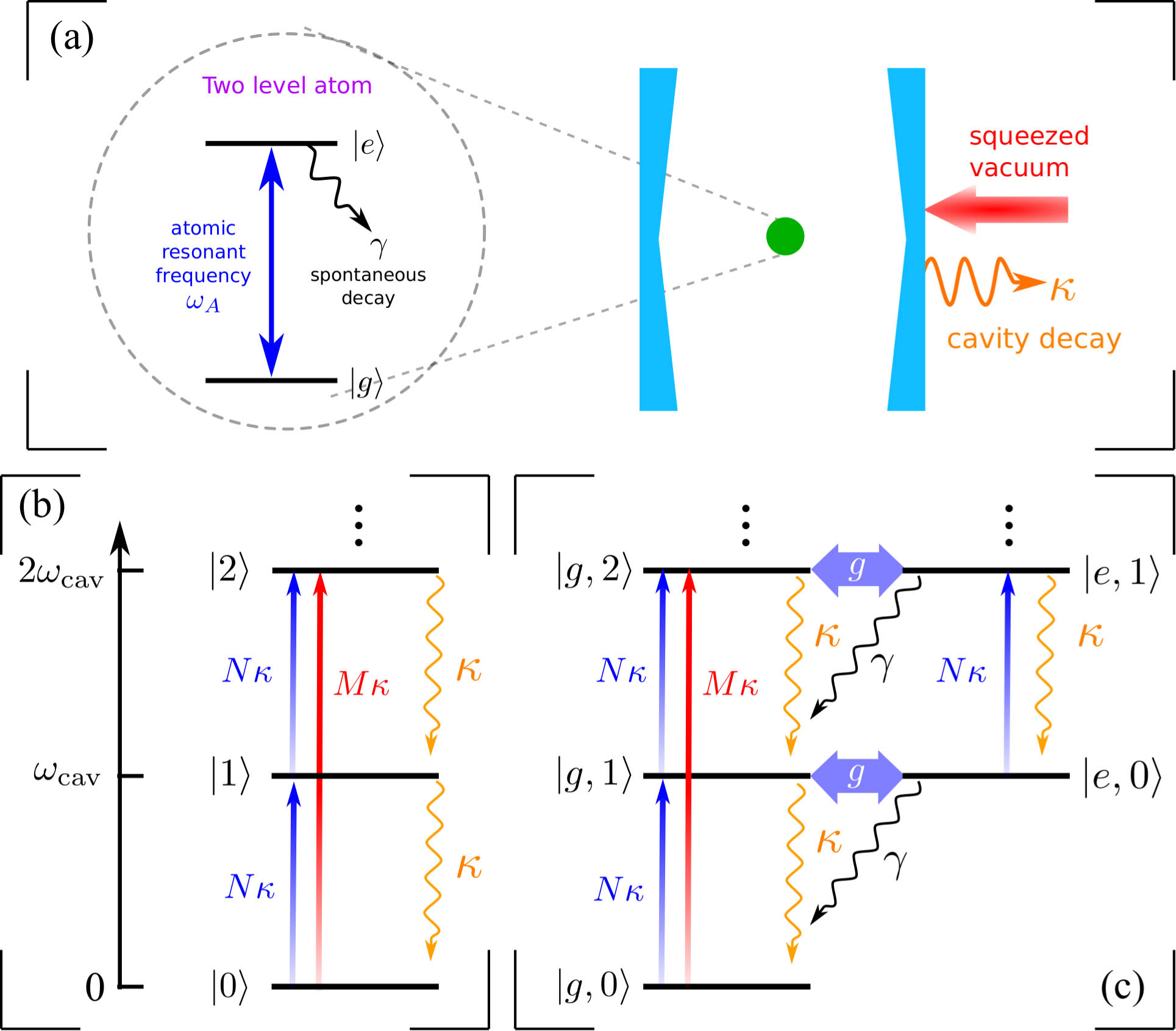
In Fig. 1(a), we first consider a two-level atom trapped in a single mode cavity with high Q, resulting in strong coupling between the cavity mode and atom. The cavity mode frequency is labeled as , and the atomic resonance frequency is labeled as , with being the energy of state . A broadband squeezed vacuum with central angular frequency is injected into the cavity, as shown in Fig. 1(a).

Figure 1.(a) Sketch of the single atom–cavity QED system driven by a broadband squeezed vacuum with central frequency . The resonance frequency of this two-level atom with being the energy of state . Here, is the coupling constant between the atom and cavity. and are the decay rates of the atom and cavity, respectively. Panels (b) and (c) demonstrate the energy levels and the corresponding transition pathways for the empty cavity and the atom–cavity QED system, respectively.
Under the electric dipole approximation, the Hamiltonian of this system can be expressed in the rotating frame of the central frequency of the squeezed field, which reads[44,45]where the atomic operator , and is the coupling constant between the atom and cavity. The annihilation and creation operators of the cavity photon are denoted by and , respectively. Here, the detunings for the atom and cavity are defined by and , respectively.
The evolution of this system, given by Eq. (1), is governed by the standard master equation[45], which is given by where is the density matrix operator. and are the damping terms for the atom and cavity, respectively. In general, they have the following forms: and with and being the damping rate of the atom and cavity, respectively. Here, is the photon number of the squeezed field, with being the squeezing parameter. denotes the two-photon correlation in the injected squeezed vacuum with being the phase of the squeezed field[46–48]. The corresponding transition pathways for an empty cavity and a single atom–cavity QED system are illustrated in Figs. 1(b) and 1(c), respectively. The squeezed vacuum driven single atom–cavity QED system, governed by Eq. (2), has been studied under the condition of a bad cavity, where the atom–cavity coupling constant [12,45]. In the following, we extend the research to the strong coupling regime, i.e., .
To begin with, we examine the cavity excitation spectrum of the empty cavity by numerically solving Eq. (2). As shown in Fig. 2(a), the mean photon number , where denotes the expected value of the operator , is independent to the squeezed vacuum frequency (blue dashed line). For the single atom–cavity QED system, it is clear to see that a dip in the cavity excitation spectrum exists when the atomic resonance frequency [see Fig. 2(a), red solid curve]. Here, we choose the system parameters as , , and . This phenomenon can be explained by comparing the transition pathways shown in Figs. 1(b) and 1(c). In the presence of the atom, the energy exchange between the cavity and atom becomes dominant when the coupling constant is strong enough. Thus, the spontaneous emission of the atom leads to a dip in the cavity excitation spectrum.

Figure 2.Panels (a) and (b) show the cavity excitation spectrum, i.e., the mean photon number , and the quantum fluctuation of cavity photons with . For the empty cavity (blue dashed curves), the cavity mode frequency is fixed, and . In the presence of the atom (red solid curves), we assume and . The system parameters are given by and .
Apart from the mean photon number, the quantum fluctuations of photons in the cavity also change significantly when the atom is strongly coupled to the cavity mode. To show this point, we plot the quantum fluctuation by taking the same system parameters used in Fig. 2(a). In the absence of the atom, the quantum fluctuations of cavity photons only exist near the central frequency of the squeezed vacuum and reach its maximum at the central frequency (see blue dashed curve). When the squeezed vacuum is off-resonance with the cavity, the fluctuations of cavity photons drop quickly, as shown in Fig. 2(b). However, in the presence of the atom, the fluctuations of cavity photons at the central frequency disappear since the energy exchange between the atom and cavity smooths the fluctuations induced by the two-photon process (red curve). When the atomic resonance frequency is detuned far away from the squeezed vacuum frequency, the fluctuations take place again. By measuring these features induced by the interaction between the atom and squeezed vacuum, it is possible to sense atoms in the cavity.
In addition, the interaction of the atom and the squeezed vacuum results in quantum destructive interference, which significantly suppresses the two-photon excitation. To show this interesting phenomenon, we consider the case of small squeezing parameter , i.e., . In this case, only the states in one- and two-photon spaces need to be considered, which result in five quantum states labeled by , , , , and , respectively. All decays, couplings, and transition pathways are shown in Fig. 3(a).

Figure 3.(a) Quantum states and transition pathways of the single atom–cavity QED system driven by a squeezed vacuum. (b) Mean photon number and probabilities of one- and two-photon excitations versus the squeezing parameter .
Using the Eq. (2), the equations of motions for elements of the density matrix are given by where the individual element of density matrix and . For weak driving field, Eq. (3) can be solved under the steady-state approximation.
Assuming , we have and . Then, inserting Eq. (4) into Eqs. (3d), (3e), and (3g), one can obtain the population in state , which reads with . Clearly, the destructive interference effect will take place when two terms on the right hand side of Eq. (5) cancel each other. Thus, the two-photon excitations will be significantly suppressed (i.e., ) for small .
To verify the above analysis, we evaluate the probability of finding photons in the Fock state by numerically solving Eq. (2) with the same system parameters used in Fig. 2. The reduced density matrix is obtained by taking partial trace with respect to the atom. As shown in Fig. 3(b), the probability of two-photon Fock state is close to zero when (see orange curve), while the probability of one-photon Fock state (see blue curve) implies that the two-photon excitation is blockaded. It is worth pointing out that, in the weak driving limit, the mean photon number so that the multiphoton excitations are also be blockaded, corresponding to .
Next, we discuss the feasibility of realizing the suppression of two-photon excitation in experiments. In Figs. 4(a) and 4(b), we take and plot the probabilities of one- and two-photon Fock states as functions of the squeezing parameter and the normalized coupling constant . It is clearly seen that the two-photon excitation can be efficiently suppressed over a wide range of coupling constant for small squeezing parameters. Thus, a robust experimental condition is available.

Figure 4.Probabilities of one- and two-photon Fock states (a) and (b) versus the squeezing parameter and the normalized coupling constant with .
For large squeezing parameter , one can obtain so that the transitions denoted by in Fig. 3(a) become as important as the transitions denoted by . Therefore, multiphoton excitations must be considered. Thus, Eq. (3) is invalid, and one has to numerically solve Eq. (2) to obtain probabilities of photon states . As shown in Fig. 5, the probability of two-photon state is enhanced significantly and has the same order of the probability of the one-photon state with the increase of the squeezing parameter . Correspondingly, the mean photon number also becomes very large, since the multiphoton processes take place.

Figure 5.Mean photon number and probabilities of one- and two-photon excitations versus the squeezing parameter .
In conclusion, we have carefully studied the single atom–cavity QED system driven by a broadband squeezed vacuum under the strong coupling regime. Due to the energy exchange between the atom and cavity, the mean photon number and quantum fluctuations of the cavity photons are significantly changed. We show that, in the presence of the atom, a dip at the central frequency of the squeezed field exists, which can be used to detect the existence of the atom. We also show that the quantum fluctuations of cavity photons disappear when the atomic resonance frequency is the same as the squeezed vacuum frequency. However, the quantum fluctuations increase significantly when the frequency of the squeezed field is detuned far away from the cavity resonant frequency. Moreover, we find that the two-photon excitations are significantly suppressed for small squeezing parameters because of the quantum destructive interference effect. We also show that this phenomenon can be easily realized with current experimental conditions and may be used to generate the single photon state. All results presented in this Letter may help readers understand how the squeezed vacuum interacts with the cavity QED system more clearly.
References
[1] H. Walther, B. T. Varcoe, B.-G. Englert, T. Becker. Rep. Prog. Phys., 69, 1325(2006).
[2] S. M. Dutra. Cavity Quantum Electrodynamics: The Strange Theory of Light in a Box(2005).
[3] Y. Zhu, D. J. Gauthier, S. Morin, Q. Wu, H. Carmichael, T. Mossberg. Phys. Rev. Lett., 64, 2499(1990).
[4] K. M. Birnbaum, A. Boca, R. Miller, A. D. Boozer, T. E. Northup, H. J. Kimble. Nature, 436, 87(2005).
[5] H. Carmichael. Phys. Rev. X, 5, 031028(2015).
[6] C. Zhu, L. Ping, Y. Yang, G. S. Agarwal. Phys. Rev. Lett., 124, 073602(2020).
[7] Y. Li, C. Zhu, L. Deng, E. Hagley, W. Garrett. Opt. Lett., 40, 5243(2015).
[8] A. Imamoglu, D. D. Awschalom, G. Burkard, D. P. DiVincenzo, D. Loss, M. Sherwin, A. Small. Phys. Rev. Lett., 83, 4204(1999).
[9] S.-B. Zheng, G.-C. Guo. Phys. Rev. Lett., 85, 2392(2000).
[10] A. Blais, R.-S. Huang, A. Wallraff, S. M. Girvin, R. J. Schoelkopf. Phys. Rev. A, 69, 062320(2004).
[11] T. Liu, G. Lin, F. Zhou, L. Deng, S. Gong, Y. Niu. Chin. Opt. Lett., 15, 092702(2017).
[12] D. F. Walls, G. J. Milburn. Quantum Optics(2007).
[13] D. Wang, J. Han, S. Zhang. Chin. Opt. Lett., 16, 050005(2018).
[14] Y. Han, C. Zhu, X. Huang, Y. Yang. Phys. Rev. A, 98, 033828(2018).
[15] A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R.-S. Huang, J. Majer, S. Kumar, S. M. Girvin, R. J. Schoelkopf. Nature, 431, 162(2004).
[16] J. Wu, C. Zhu, Y. Yang. Opt. Lett., 40, 4975(2015).
[17] M. Mücke, E. Figueroa, J. Bochmann, C. Hahn, K. Murr, S. Ritter, C. J. Villas-Boas, G. Rempe. Nature, 465, 755(2010).
[18] Y. Zhu. Opt. Lett., 35, 303(2010).
[19] C. Zhu, G. Huang. Opt. Express, 19, 23364(2011).
[20] G. Kirchmair, B. Vlastakis, Z. Leghtas, S. E. Nigg, H. Paik, E. Ginossar, M. Mirrahimi, L. Frunzio, S. M. Girvin, R. J. Schoelkopf. Nature, 495, 205(2013).
[21] C. Zhu, L. Deng, E. W. Hagley. Phys. Rev. A, 90, 063841(2014).
[22] Y. Zhang, Z. Zhu, Z. Peng, C. Jiang, Y. Chai, L. Tan. Chin. Opt. Lett., 16, 012701(2018).
[23] R. Li, C. Zhu, L. Deng, E. W. Hagley. Appl. Phys. Lett., 105, 161103(2014).
[24] K. Hou, D.-Q. Bao, C.-J. Zhu, Y.-P. Yang. Quantum Inf. Process., 18, 104(2019).
[25] M. O. Scully, M. S. Zubairy. Quantum Optics(1999).
[26] H. J. Metcalf, P. van der Straten. The Optics Encyclopedia: Basic Foundations and Practical Applications(2007).
[27] C. J. Pethick, H. Smith. Bose–Einstein Condensation in Dilute Gases(2008).
[28] H. J. Kimble. Phys. Scr., T76, 127(1998).
[29] A. Kubanek, A. Ourjoumtsev, I. Schuster, M. Koch, P. W. Pinkse, K. Murr, G. Rempe. Phys. Rev. Lett., 101, 203602(2008).
[30] A. Boca, R. Miller, K. Birnbaum, A. Boozer, J. McKeever, H. Kimble. Phys. Rev. Lett., 93, 233603(2004).
[31] C. Hamsen, K. N. Tolazzi, T. Wilk, G. Rempe. Phys. Rev. Lett., 118, 133604(2017).
[32] C. Zhu, Y. Yang, G. Agarwal. Phys. Rev. A, 95, 063842(2017).
[33] M.-O. Pleinert, J. von Zanthier, G. S. Agarwal. Optica, 4, 779(2017).
[34] R. Huang, A. Miranowicz, J.-Q. Liao, F. Nori, H. Jing. Phys. Rev. Lett., 121, 153601(2018).
[35] N. P. Georgiades, E. Polzik, K. Edamatsu, H. Kimble, A. Parkins. Phys. Rev. Lett., 75, 3426(1995).
[36] D. Toyli, A. Eddins, S. Boutin, S. Puri, D. Hover, V. Bolkhovsky, W. Oliver, A. Blais, I. Siddiqi. Phys. Rev. X, 6, 031004(2016).
[37] S. Kono, Y. Masuyama, T. Ishikawa, Y. Tabuchi, R. Yamazaki, K. Usami, K. Koshino, Y. Nakamura. Phys. Rev. Lett., 119, 023602(2017).
[38] D. Bao, C. Zhu, Y. Yang, G. Agarwal. Opt. Express, 27, 15540(2019).
[39] A. Kowalewska-Kudłaszyk, S. I. Abo, G. Chimczak, J. Peřina, F. Nori, A. Miranowicz. Phys. Rev. A, 100, 053857(2019).
[40] P. Grangier, R. Slusher, B. Yurke, A. LaPorta. Phys. Rev. Lett., 59, 2153(1987).
[41] J. Appel, E. Figueroa, D. Korystov, M. Lobino, A. Lvovsky. Phys. Rev. Lett., 100, 093602(2008).
[42] F. Wolfgramm, A. Cere, F. A. Beduini, A. Predojević, M. Koschorreck, M. W. Mitchell. Phys. Rev. Lett., 105, 053601(2010).
[43] U. L. Andersen, T. Gehring, C. Marquardt, G. Leuchs. Phys. Scr., 91, 053001(2016).
[44] K. Hou, C. Zhu, Y. Yang, G. Agarwal. Phys. Rev. A, 100, 063817(2019).
[45] G. S. Agarwal. Quantum Optics(2012).
[46] P. R. Rice, L. M. Pedrotti. J. Opt. Soc. Am. B, 9, 2008(1992).
[47] G.-X. Li, K. Allaart, D. Lenstra. Phys. Rev. A, 69, 055802(2004).
[48] G.-X. Li, Y.-P. Yang, K. Allaart, D. Lenstra. Phys. Rev. A, 69, 014301(2004).
![]()
![]()
![]()
![]()
![]()