Photon pair generation from lithium niobate metasurface with tunable spatial entanglement [Invited]

Jihua Zhang; Jinyong Ma; Dragomir N. Neshev; Andrey A. Sukhorukov

doi:10.3788/COL202321.010005

Abstract

The two-photon state with spatial entanglement is an essential resource for testing fundamental laws of quantum mechanics and various quantum applications. Its creation typically relies on spontaneous parametric downconversion in bulky nonlinear crystals where the tunability of spatial entanglement is limited. Here, we predict that ultrathin nonlinear lithium niobate metasurfaces can generate and diversely tune spatially entangled photon pairs. The spatial properties of photons including the emission pattern, rate, and degree of spatial entanglement are analyzed theoretically with the coupled mode theory and Schmidt decomposition method. We show that by leveraging the strong angular dispersion of the metasurface, the degree of spatial entanglement quantified by the Schmidt number can be decreased or increased by changing the pump laser wavelength and a Gaussian beam size. This flexibility can facilitate diverse quantum applications of entangled photon states generated from nonlinear metasurfaces.

Keywords

metasurface spatial entanglement spontaneous parametric downconversion

1. Introduction

Entanglement is an important feature of quantum mechanics that underpins various applications of quantum technologies^[1]. In particular, photon pairs that are entangled in the high-dimensional spatial space represent an essential resource in a broad range of quantum applications, including imaging^[2,3], communications^[4], and computations^[5]. The performance of such applications is related to the degree of entanglement. The most common way to generate spatially entangled photon pairs is based on the spontaneous parametric downconversion (SPDC) in quadratic nonlinear crystals, where a pump photon spontaneously splits into two lower-energy photons in two different directions^[6]. The properties of generated states, including the emission pattern and spatial entanglement, have been extensively investigated^[7–9]. For nonlinear crystals with a typical thickness on the scale of millimeters to centimeters, the stringent phase-matching condition limits the emission directions of the photon pairs to a certain predefined angle range, making it difficult to flexibly tune the spatial pattern and entanglement of the photon pairs while maintaining generation efficiency. Although control of spatial correlations of the photon pairs was recently reported by engineering the pump beam profile^[10], the specific tuning range of the spatial entanglement was unknown. It was shown that strong multimode entanglement can be achieved in thin nonlinear films^[11]; however, the generation efficiency was much weaker compared to conventional schemes. Thereby, it remained a challenge on how to efficiently generate tunable spatially entangled photon pairs.

Recently, it was shown experimentally that metasurfaces in the form of nanostructured layers supporting optical resonances^[12–17] can boost photon pair generation^[18–21]. Furthermore, it was demonstrated that a lithium niobate metasurface featuring nonlocal guided mode resonances can generate spatially entangled photon pairs in a broad angle range^[20]. In this work, we provide a theoretical description of the two-photon state generated from metasurfaces and a quantitative study on its degree of spatial entanglement, based on the Schmidt decomposition approach. By taking advantage of the strong angular dispersion of the nonlocal metasurface, we predict that the emission pattern of the photon pairs can be varied by simply changing the wavelength or beam size of the pump laser. This represents a simple and effective way to generate photon states with tunable spatial entanglement from ultrathin metasurfaces, which may find applications in advanced quantum imaging and communications.

2. SPDC from Lithium Niobate Nonlocal Metasurface

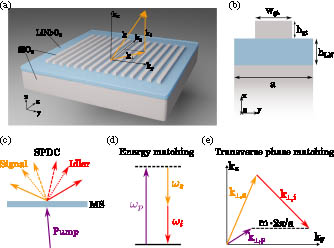
We consider the metasurface design following the experimental platform described in Ref. [20]. As shown in Figs. 1(a) and 1(b), it is based on an $x$ -cut lithium niobate ( ${LiNbO}_{3}$ ) thin film (thickness $h_{LN} = 304 nm$ ) covered by a silicon dioxide ( ${SiO}_{2}$ ) grating with a period $a = 890 nm$ , width $w_{gt} = 550 nm$ , and thickness $h_{gt} = 200 nm$ . The optical axis of the ${LiNbO}_{3}$ and the grating are along the in-plane $z$ direction. In the SPDC process, a pump photon splits into two photons, called signal and idler photons. This metasurface supports nonlocal guided mode resonance at the signal and idler wavelengths around 1570 nm, which facilitates an increased density of states and boosts the SPDC process.

Sign up for Chinese Optics Letters TOC. Get the latest issue of Chinese Optics Letters delivered right to you！Sign up now

Figure 1.(a) Schematic of the proposed metasurface consisting of a silicon dioxide grating on top of a lithium niobate thin film on a silicon dioxide substrate. The yellow arrow k defines the wave vector of the emitted photons. k_⊥ and k_∥ are the transverse and longitudinal components of the wave vector, respectively. (b) Cross section of one unit cell of the metasurface; (c) wide-angle emission of photons from the subwavelength-thick metasurface, satisfying (d) energy matching and (e) transverse phase matching.

Importantly, due to the subwavelength thickness of the metasurface, the longitudinal phase matching is relaxed, allowing SPDC in a broad anglular range, as shown in Fig. 1(c). The frequencies and wave vectors of the photons satisfy the following energy and transverse phase-matching conditions, as illustrated in Figs. 1(d) and 1(e), $ω_{s} + ω_{i} = ω_{p},$ (1) $k_{⊥, s} + k_{⊥, i} + m \cdot 2 π / a \hat{y} = k_{⊥, p},$ (2)where $ω_{p}$ , $ω_{s}$ , and $ω_{i}$ are the angular frequencies of the pump, signal, and idler photons, $k_{⊥, p}$ , $k_{⊥, s}$ , and $k_{⊥, i}$ are their transverse wave vectors in the $y - z$ plane, and $m$ is an integer. For a specific pump, matching these two conditions means that if the frequency or angle of one photon is known, the information for another photon is determined automatically. This essentially leads to the frequency and spatial correlations of the photon pairs. In the following, we consider the case of $m = 0$ corresponding to the experimental conditions in Ref. [20]. For grating periods larger than the signal/idler wavelengths and allowing for high-order diffraction with nonzero $m$ , one can anticipate new features in spatial entanglement, which goes beyond the scope of the current paper. The resulting two-photon state has a wave function, $| Ψ 〉 = \int d ω_{s} d ω_{i} d k_{⊥, s} d k_{⊥, i} S (ω_{s} + ω_{i}, k_{⊥, s} + k_{⊥, i}) \cdot Ξ (ω_{s}, k_{⊥, s}; ω_{i}, k_{⊥, i}) | ω_{s}, k_{⊥, s} 〉 | ω_{i}, k_{⊥, i} 〉,$ (3)where $S$ is the normalized frequency-angular spectrum of the pump light. $Ξ (ω_{s}, k_{⊥, s}; ω_{i}, k_{⊥, i})$ is the SPDC efficiency function.

The wave function is controllable by the spectrum of the pump, similar to the case in conventional nonlinear crystals^[10]. Note that this control is weighted by the SPDC efficiency function. The difference in metasurfaces is that the SPDC is free from longitudinal phase matching, and its efficiency is fully determined by the frequency and angular dispersion of the optical resonances. This feature enables control of the spatial properties of the photon pairs by engineering optical resonances supported by the metasurface. For example, in the proposed metasurface with angular-dependent nonlocal resonances, the photon-pair emission pattern is very sensitive to the frequency and angular spectra of the pump. In contrast, the SPDC efficiency in bulky nonlinear crystals is limited by the longitudinal phase matching, being proportional to $sinc (| δ k_{∥} | L / 2)$ , where $L$ is the thickness of the crystal and $δ k_{∥} = k_{∥, p} - (k_{∥, s} + k_{∥, i})$ is the longitudinal phase mismatch^[22,23].

3. Quantum-Classical Correspondence

The theoretical modeling of quantum photon-pair generation through SPDC in quadratically nonlinear metasurfaces can be performed through the general Green’s function formalism^[24]. A mathematically equivalent approach, which can be more convenient for numerical modeling, is based on the quantum-classical correspondence [Fig. 2(a)], where the SPDC efficiency is derived from its classical reverse process called sum-frequency generation (SFG)^{[18,20,25–28]}, $Ξ (ω_{s}, k_{⊥, s}; ω_{i}, k_{⊥, i}) = \sqrt{\frac{ω_{s} ω_{i}}{ω_{p}^{2} {(2 π)}^{3}}} ξ_{SFG} (ω_{s}, - k_{⊥, s}; ω_{i}, - k_{⊥, i}) .$ (4)

Figure 2.(a) Quantum-classical correspondence between the SPDC and SFG; (b) CMT-predicted resonance wavelengths of the metasurface as a function of the transverse wave vector k_y at k_z = 0; (c)–(f) SFG efficiency as a function of the signal wavelength calculated by CMT (black circles) and COMSOL simulation (red lines) for different input transverse wave vectors of the signal (k_y,s = 0, 0.025 rad/µm) and wavelengths of the pump. The double of the pump wavelength is (c)–(d) 1569.84 nm and (e)–(f) 1567.33 nm, which are marked by the black dashed lines in (b).

Here, $ξ_{SFG} (ω_{s}, - k_{⊥, s}; ω_{i}, - k_{⊥, i}) = A_{p} / (A_{s} A_{i})$ is the SFG efficiency in the reverse direction, with $A_{p}$ being the output SFG and $A_{s}$ ( $A_{i}$ ) being the input signal (idler) complex amplitudes of unit intensity plane waves. In this work, we are interested in the angular or spatial properties of the photons and consider a continuous-wave pump. Here we focus on the case of degenerate SPDC ( $ω_{s} = ω_{i} = 0.5 ω_{p}$ ), since the frequency spectrum of photons was found to be narrow^[20]. This is because the degenerate SPDC efficiency is much stronger than in the nondegenerate case, as we show in Section 3. The corresponding spatial wave function becomes $| Ψ 〉 = \int d k_{⊥, s} d k_{⊥, i} \frac{S (k_{⊥, s} + k_{⊥, i})}{4 π} ξ_{SFG} (- k_{⊥, s}; - k_{⊥, i}) | k_{⊥, s} 〉 | k_{⊥, i} 〉 .$ (5)

After calculating this two-photon wave function, we can reveal the emission brightness and pattern of the SPDC and the spatial entanglement of the photon pairs. Apparently, they are controllable through the angular spectrum of the pump and the angular-dependent SFG efficiency determined by the optical resonance of the metasurface. The complexity of Eq. (5) comes from the fact that for a specific pump, the photon pairs from the metasurface can emit to all directions satisfying the transverse phase-matching conditions in Eq. (2). As a result, one needs to simulate the SFG process in all directions to simulate the full SPDC process, which is a computationally demanding task.

4. Coupled Mode Theory for SPDC Modeling

To efficiently model the SPDC process in the lithium niobate metasurface, we have proposed a coupled mode theory (CMT) that can accurately calculate the frequency and angular dispersion of the guided mode resonances in the metasurface (see detailed theory in the Supplementary Material of Ref. [20]). Figure 2(b) shows the CMT predicted resonance wavelengths of the metasurface at different transverse wave vectors along the $y$ direction. Based on the CMT, we can also calculate the SFG efficiencies for different $k_{y, s}$ and pump wavelengths $λ_{p}$ . Note that the guided mode resonance and SFG efficiency has a weak dependence on $k_{z, s}$ , and thus we only consider the case of $k_{z, s} = 0$ here. In the SFG simulations, we calculate the generated pump with a fixed frequency ( $ω_{p}$ ) and emitting along the normal direction ( $k_{⊥, p} = 0$ ) such that $ω_{i} = ω_{p} - ω_{s}$ and $k_{y, i} = - k_{y, s}$ in each simulation. As shown in Figs. 2(c)–2(f), the CMT results show a good agreement with the full-wave simulations conducted in COMSOL Multiphysics, confirming its high accuracy in modeling SFG and the corresponding SPDC process based on Eq. (5). Importantly, the COMSOL simulation takes around 1 h to calculate 500 points of the signal wavelength, while the CMT takes only 14 ms. Note that the SFG efficiencies in Figs. 2(c) and 2(f) are about an order of magnitude higher than the ones in Figs. 2(d) and 2(e). This is because in Figs. 2(c) and 2(f), the degenerate signal and idler photons are both at resonance wavelength, while only either a signal or idler photon is resonant for the nondegenerate case in Figs. 2(d) and 2(e). Due to the quantum-classical correspondence, we expect that the degenerate SPDC efficiency is the strongest in the specific direction determined by the pump wavelength. Therefore, only the frequency-degenerate SPDC is considered in the following analysis of the spatial entanglement of the photon pairs.

5. Quantification of Spatial Entanglement

We now calculate SFG at the degenerate wavelength for different wave vectors and obtain the two-photon wave function of the photons based on Eq. (5). Specifically, we consider a Gaussian pump beam with an angular spectrum $S (k_{⊥}) = \exp (- σ_{p}^{2} {| k_{⊥} |}^{2} / 4)$ , where $σ_{p}$ is the beam waist radius. Note that a normally incident Gaussian pump beam is effectively composed of infinitely obliquely incident plane waves with a nonzero $k_{⊥}$ . By integrating over the wave vector, we obtain the spectral brightness of the SPDC, as shown in Fig. 3(a) for different pump wavelengths and beam radii. In the calculation, an upper bound of 0.05 rad/µm has been applied for $k_{y}$ and $k_{z}$ , which corresponds to a collection angle of 0.7 deg in a previous experimental setup^[20]. One can see that for each beam size, there is a peak for the SPDC at $2 λ_{p} = 1569.1 nm$ , which is slightly blueshifted from the resonance at normal incidence. We notice that the highest brightness occurs at $σ_{p} = 45 µm$ . This is because the generation rate of photon pairs depends on the incident angle of the plane-wave pump and the maximum happens near $k_{y, p} = 0.015 rad / µm$ , as shown by Fig. S3d in the Supplementary Material of Ref. [20]. The pump beam with a radius of $σ_{p} = 45 µm$ has the largest weight at the wave vector components near this value.

Figure 3.(a) SPDC brightness at the degenerate wavelength and (b) Schmidt number of the emitted photons as a function of the pump laser wavelength and Gaussian beam radius. Point A in (b) marks the peak Schmidt number at pump wavelength of 784.15 nm and beam radius of 200 µm. Point B corresponds to the same pump wavelength with a beam radius of 5 µm. (c), (d) SPDC emission patterns corresponding to the points A and B in (b), as indicated by labels.

We perform a Schmidt decomposition of the two-photon wave function to quantify the spatial entanglement. The Schmidt decomposition of the wave function vector is performed, and the related Schmidt coefficients ( $s_{m}$ ) and modes are obtained by using the open source MATLAB code QETLAB. The related Schmidt numbers are calculated by $\sum_{m} s_{m}^{4}$ and shown in Fig. 3(b). Obviously, the Schmidt number is strongly dependent on the wavelength and beam size of the pump and can be tuned in a large range from 1.1 (weakly entangled) to 20 (strongly entangled). A larger beam radius leads to a larger Schmidt number. This is reasonable, since a plane-wave pump with an infinite beam radius has a single transverse wave vector, resulting in photon pairs with fully deterministic relation between the signal and idler wave vectors according to the transverse phase matching, and each of a continuum number of such pairs represents a Schmidt mode. For the beam radius of 200 µm, the maximum Schmidt number is found to be 20 when the pump wavelength is 784.15 nm, as marked by point $A$ in Fig. 3(b). At the same pump wavelength, the Schmidt number is only 1.1 for a pump radius of 5 µm, which is point $B$ in Fig. 3(b). The related SPDC emission patterns for these two points are shown in Figs. 3(c) and 3(d), respectively.

To gain more insight into the spatial entanglement in Fig. 3(b), we focus on the Schmidt decomposition results at points $A$ ( $λ_{p} = 784.15 nm$ , $σ_{p} = 200 µm$ ) and $B$ ( $λ_{p} = 784.15 nm$ , $σ_{p} = 5 µm$ ). Figure 4 depicts the Schmidt coefficients of the lowest 50 Schmidt modes and the mode distributions of the lowest four modes for point $A$ . As can be seen, all the 50 Schmidt coefficients are nonzero, and the first four modes have similar magnitudes, indicating a high degree of spatial entanglement. The results for point $B$ in Fig. 3(b) are shown in Fig. 5. The Schmidt coefficients show a fast drop for higher-order modes and are close to zero for the modes with a mode number over 3, confirming a weak entanglement at point $B$ .

Figure 4.(a) Schmidt coefficients of the first 50 Schmidt modes corresponding to the point A in Fig. 3(b); (b)–(e) normalized amplitude and phase distributions of the first four Schmidt modes.

Figure 5.(a) Schmidt coefficients of the first 50 Schmidt modes corresponding to the point B in Fig. 3(b); (b)–(e) normalized amplitude and phase distributions of the first four Schmidt modes.

6. Conclusions

In conclusion, we have theoretically investigated the generation of spatially entangled photon pairs via SPDC from a lithium niobate metasurface. By quantifying the spatial entanglement with the Schmidt number, we have shown that the degree of spatial entanglement can be diversely tuned by the pump laser wavelength and beam size. The capability to realize an arbitrary degree of spatial entanglement can find applications in quantum imaging, whose resolution is related to the spatial entanglement of the photon source. In the future, pump beams with tailored spatial and temporal profiles and metasurfaces with different optical resonances can be further explored to tune both the emission pattern and spatial entanglement.

References

[1] R. Horodecki, P. Horodecki, M. Horodecki, K. Horodecki. Quantum entanglement. Rev. Mod. Phys., 81, 865(2009).

[2] Y. H. Shih. Quantum imaging. IEEE J. Sel. Top. Quantum Electron., 13, 1016(2007).

[3] P. A. Moreau, E. Toninelli, T. Gregory, M. J. Padgett. Imaging with quantum states of light. Nat. Rev. Phys., 1, 367(2019).

[4] N. Gisin, R. Thew. Quantum communication. Nat. Photon., 1, 165(2007).

[5] C. H. Bennett, D. P. DiVincenzo. Quantum information and computation. Nature, 404, 247(2000).

[6] C. Couteau. Spontaneous parametric down-conversion. Contemp. Phys., 59, 291(2018).

[7] C. K. Law, J. H. Eberly. Analysis and interpretation of high transverse entanglement in optical parametric down conversion. Phys. Rev. Lett., 92, 127903(2004).

[8] S. P. Walborn, C. H. Monken, S. Padua, P. H. S. Ribeiro. Spatial correlations in parametric down-conversion. Phys. Rep., 495, 87(2010).

[9] F. M. Miatto, H. D. Pires, S. M. Barnett, M. P. van Exter. Spatial Schmidt modes generated in parametric down-conversion. Eur. Phys. J. D, 66, 263(2012).

[10] P. Boucher, H. Defienne, S. Gigan. Engineering spatial correlations of entangled photon pairs by pump beam shaping. Opt. Lett., 46, 4200(2021).

[11] C. Okoth, E. Kovlakov, F. Bonsel, A. Cavanna, S. Straupe, S. P. Kulik, M. V. Chekhova. Idealized Einstein-Podolsky-Rosen states from non-phase-matched parametric down-conversion. Phys. Rev. A, 101, 011801(2020).

[12] W. T. Chen, A. D. Y. Zhu, F. Capasso. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater., 5, 604(2020).

[13] A. S. Solntsev, G. S. Agarwal, Y. Y. Kivshar. Metasurfaces for quantum photonics. Nat. Photon., 15, 327(2021).

[14] C. L. Li, P. Yu, Y. J. Huang, Q. Zhou, J. Wu, Z. Li, X. Tong, Q. Y. Wen, H. C. Kuo, Z. M. M. Wang. Dielectric metasurfaces: from wavefront shaping to quantum platforms. Prog. Surf. Sci., 95, 100584(2020).

[15] L. Y. Chen, Z. C. Li, H. Cheng, J. G. Tian, S. Q. Chen. Progress of metasurface-enabled preparation and manipulation of quantum states. Acta Opt. Sin., 41, 0823016(2021).

[16] J. Liu, M. Q. Shi, Z. Chen, S. M. Wang, Z. L. Wang, S. N. Zhu. Quantum photonics based on metasurfaces. Opto-Electron. Adv., 4, 200092(2021).

[17] X. S. Zhu, J. Liu, J. Z. He, S. M. Wang, Z. L. Wang, S. N. Zhu. Research and application of metasurfaces in quantum optics. Acta Opt. Sin., 42, 0327006(2022).

[18] G. Marino, A. S. Solntsev, L. Xu, V. F. Gili, L. Carletti, A. N. Poddubny, M. Rahmani, D. A. Smirnova, H. T. Chen, A. Lemaitre, G. Q. Zhang, A. V. Zayats, C. De Angelis, G. Leo, A. A. Sukhorukov, D. N. Neshev. Spontaneous photon-pair generation from a dielectric nanoantenna. Optica, 6, 1416(2019).

[19] T. Santiago-Cruz, A. Fedotova, V. Sultanov, M. A. Weissflog, D. Arslan, M. Younesi, T. Pertsch, I. Staude, F. Setzpfandt, M. Chekhova. Photon pairs from resonant metasurfaces. Nano Lett., 21, 4423(2021).

[20] J. Zhang, J. Ma, M. Parry, M. Cai, R. Camacho-Morales, L. Xu, D. N. Neshev, A. A. Sukhorukov. Spatially entangled photon pairs from lithium niobate nonlocal metasurfaces. Sci. Adv., 8, eabq4240(2022).

[21] T. Santiago-Cruz, S. D. Gennaro, O. Mitrofanov, S. Addamane, J. Reno, I. Brener, M. V. Chekhova. Resonant semiconductor metasurfaces for generating complex quantum states. Science, 377, 991(2022).

[22] C. H. Monken, P. H. S. Ribeiro, S. Padua. Transfer of angular spectrum and image formation in spontaneous parametric down-conversion. Phys. Rev. A, 57, 3123(1998).

[23] M. Unternahrer, B. Bessire, L. Gasparini, M. Perenzoni, A. Stefanov. Super-resolution quantum imaging at the Heisenberg limit. Optica, 5, 1150(2018).

[24] A. N. Poddubny, I. V. Iorsh, A. A. Sukhorukov. Generation of photon-plasmon quantum states in nonlinear hyperbolic metamaterials. Phys. Rev. Lett., 117, 123901(2016).

[25] L. G. Helt, M. J. Steel. Effect of scattering loss on connections between classical and quantum processes in second-order nonlinear waveguides. Opt. Lett., 40, 1460(2015).

[26] F. Lenzini, A. N. Poddubny, J. Titchener, P. Fisher, A. Boes, S. Kasture, B. Haylock, M. Villa, A. Mitchell, A. S. Solntsev, A. A. Sukhorukov, M. Lobino. Direct characterization of a nonlinear photonic circuit’s wave function with laser light. Light Sci. Appl., 7, 17143(2018).

[27] F. Kaneda, J. Oikawa, M. Yabuno, F. China, S. Miki, H. Terai, Y. Mitsumori, K. Edamatsu. Spectral characterization of photon-pair sources via classical sum-frequency generation. Opt. Express, 28, 38993(2020).

[28] M. Parry, A. Mazzanti, A. Poddubny, G. Della Valle, D. N. Neshev, A. A. Sukhorukov. Enhanced generation of nondegenerate photon pairs in nonlinear metasurfaces. Adv. Photon., 3, 055001(2021).