- High Power Laser Science and Engineering
- Vol. 8, Issue 4, 04000e44 (2020)
Abstract
1 Introduction
The interaction of intense femtosecond (fs) laser radiation with atoms/molecules may lead to a substantial distortion of the atomic/molecular potentials and intrinsic dynamics. A well-known result of such a distortion is the so-called tunneling ionization that underlies processes such as high harmonic generation (HHG)[1] and above-threshold ionization (ATI)[2]. Tunneling ionization occurs when an infrared (IR) pulse is distorting the Coulomb potential of the system, forming potential barriers that oscillate with the laser period, through which an electron can tunnel out into the continuum. Whether tunneling or multiphoton is the main mechanism of photoionization depends on the interplay between the radiation’s field strength, frequency, pulse duration as well as the ionization energy of the atom/molecule. The key parameter that defines the mechanism underlying a photoionization process is the Keldysh or adiabatic parameter[3]
 (1)
(1) (2)
(2) (3)
(3)If
2 Nonresonant strong XUV field effects
In order to induce nonlinear effects in the XUV region a powerful source is required[7]. Recently, a 20 GW XUV attosecond (as) beamline has been demonstrated at Foundation for Research and Technology - Hellas (FORTH), a detailed description of which can be found in the work of Nayak et al.[8] and Makos et al.[9]. In this beamline
Sign up for High Power Laser Science and Engineering TOC. Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
A more accurate evaluation of the shifts due to the XUV radiation field strength is obtained by solving the helium time-dependent Schrödinger equation (TDSE). The radiation field used in the calculation modeled the temporal profile of the electric field with a Gaussian envelope,
 (4)
(4)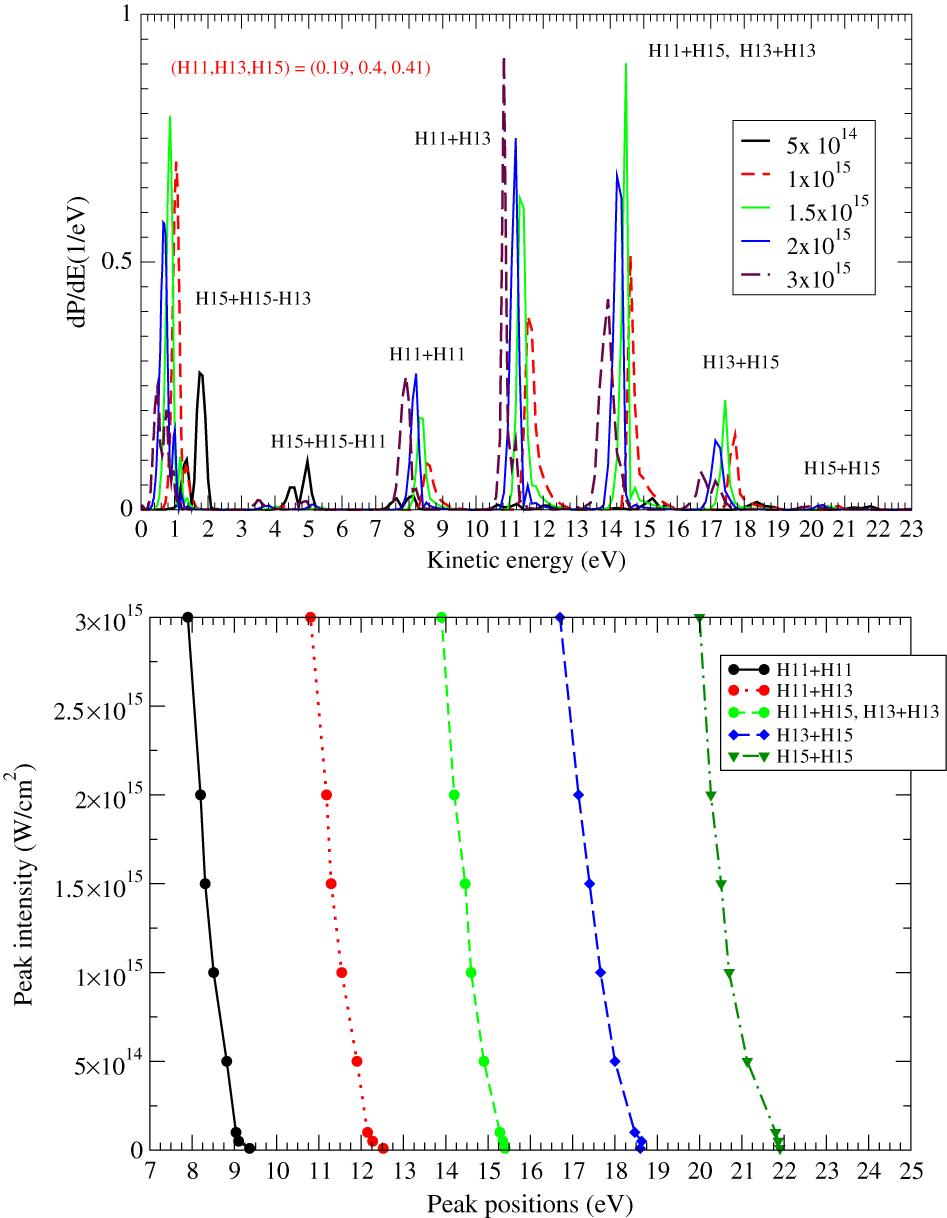
Figure 1.PES of the two-photon He ionization by a pulse train of an envelope  fs, pulse duration
fs, pulse duration  as, synthesized by the 11th–15th harmonics with relative intensities 0.19:0.4:0.41, respectively, for different total XUV intensities ranging from
as, synthesized by the 11th–15th harmonics with relative intensities 0.19:0.4:0.41, respectively, for different total XUV intensities ranging from  W/cm
W/cm to
to  W/cm
W/cm (top plot); PES peak shifts as a function of the total XUV intensity in the interval ranging from 0 to
(top plot); PES peak shifts as a function of the total XUV intensity in the interval ranging from 0 to  W/cm
W/cm (bottom plot).
(bottom plot).
3 Resonant strong XUV field effects
![]()
Figure 2.XUV EIT schemes in He through coupling of a bound with (a) an AIS or (b) two AISs.
In an alternative ionization scheme, in order to better match the pulse duration with the width of the coupled states, the 5th harmonic of the SYLOS laser is resonantly coupling the 2s
![]()
Figure 3.A VUV LICS scheme in He probed by an XUV field.
In all of the coupling schemes described previously, detuning is well within the bandwidth of the harmonics considered for the parameters of the ELI-ALPS SYLOS laser. The examples described previously can be implemented using variable delays between the two radiation fields, thus examining the dynamics of the effects and controlling the intensities used. From the technical point of view, the required two colors can be selected using either filters or multilayer mirrors. It is common practice in XUV delay lines that bisected reflecting optics are used. Different filtering coatings or different multilayer mirrors used in the two parts of the optics allow for selection of the required harmonics, while maintaining their pulse duration.
Such types of experiments can of course be implemented in other laser laboratories as well, provided that the required XUV intensities and bandwidths are available and for certainty in FEL infrastructures. In fact, EIT-related experiments dealing with core resonant Auger decays have been modeled theoretically[29,30].
4 Experimental considerations
Successful implementation of the kind of experiments described in the previous sections is subject to bypassing a number of obstacles. Availability of high intensities is the first prerequisite. For FEL sources this is less of an issue. For laser-driven harmonic sources, high enough intensities are available in the low photon energy XUV spectral region, i.e., up to 25–30 eV. At higher photon energies there is a potential, but no experimental demonstrations exist at present.
![]()
Figure 4.Photoelectron peak shifts observed with ionizing XUV intensity in single-photon ionization of Ar. Xe gas was utilized as the generating medium and a Sn filter was used for spectral selection. The spectra are obtained at two different XUV energies, measured by a calibrated XUV photodiode: 1.8 μJ/pulse (upper black line, shifted in
![]()
Figure 5.Harmonic spectra recorded by a flat-field XUV spectrometer (FFS) varying the peak gas density of Xe at the harmonic generation region:  cm
cm (upper black line, shifted in
(upper black line, shifted in  cm
cm (lower red line). The observed blueshift is of the order of
(lower red line). The observed blueshift is of the order of  eV.
eV.
5 Theoretical challenges for ionization processes in XUV intense fields
Following the introduction of the chirped-pulse amplification technique in the mid-1980s, the nonlinear interaction of atomic systems with visible laser fields has been studied extensively in great detail, both experimentally and theoretically. These studies resulted in the observation of a number of novel physical processes, such as ATI, HHG, and tunneling ionization. With the laser’s photon frequency relatively restricted to the long-wavelength scale (e.g., Ti:sapphire) the central factors allowing for these processes to show up experimentally are the strength and the ultrashort duration of the radiation field. In fact, ATI measurements require both intense (
Although the fundamental principles for the interaction of radiation and atomic/molecular systems remain the same as in the visible/IR regime, the relatively high-frequency (or shorter wavelength) of the XUV fields entails qualitatively and quantitatively distinct observations; some of them are so essential that they present certain experimental and theoretical challenges. An exclusive physical feature of the atomic interactions with fields of shorter wavelength is the possibility of excitation of inner-shell electrons (in the X-ray regime these are the prominent ionization channels); in contrast to the optical radiation where the excitation involves exclusively the valence electrons. In other words, the outer shell effectively constitutes an opaque shield for the inner-shell electrons against the visible/IR radiation. In contrast, the short-wavelength radiation at the higher-energy XUV regime, causes (with high probability) inner-shell or double-electron excitations to unstable continuum resonances, eventually leading to the system’s autoionization. Such a type of continuum excitation transitions can also be seen as ionization via an intermediate state (short-lived), which, depending on the atomic system and the radiation properties, perhaps competes with direct photoionization. It is also observed that for short-wavelength radiation, tunneling, ATI ionization and harmonic generation radiation are significantly suppressed.
From a theoretical standpoint this wavelength regime necessitates a more detailed knowledge of the atomic structure, but on the other hand standard nonperturbative features of these interactions require very high intensities, not easily reached except in FEL facilities; for example, for the UV radiation (
5.1 TDSE
In this context, the theoretical description (and the associated numerical algorithms and computational implementation) of nonlinear UV/XUV processes is a demanding problem. To date, such calculations using a broad range of radiation parameters, have been thoroughly performed only for hydrogen- and helium-like systems and with a lesser degree for the light noble gases, Ar and Ne.
For the current purposes of UV/XUV fields, we briefly present the main expressions for the TDSE of an N-electron atomic system in a laser field, described by an electric field of a spatiotemporal profile,
 (5)
(5) (6)
(6)One method to calculate the solution of Equation (5) requires the expansion of the system’s time-dependent wavefunction on its eigenstates,
 (7)
(7)The eigenstates
 (8)
(8) (9)
(9)A major simplification for the solution of Equation (8) is possible, because the wavelength of the UV/XUV pulse is much larger than the atomic scale. In this case one may solve the TDSE by dividing the interaction region into subregions of constant intensity, by setting fixed conditions on the
 (10)
(10)Calculations that take into account the spatial distribution of the radiation beam are usually required when ionization saturation is starting to set in, as resonance conditions could be satisfied at various beam positions and time intervals. Accordingly, the time profile of the pulse (or, equivalently, the frequency spectrum) may cause time-dependent resonance conditions. The calculations shown in Figure 1 provide the photoelectron energy distributions for various intensities by solving the TDSE of helium in the pulse train discussed in Section 2. In these calculations no volume integration (in the sense of Equation (10)) has taken place. Thus, they represent the ionization yield produced at the pulse focus.
5.2 Time-dependent perturbation theory
Depending on the experimental conditions that include the setup, the radiation field, and the atomic system, simplifications of the TDSEs may be possible, namely by employing a perturbative formulation. Apart from the relative strength between the interaction potential and the atomic energies (see discussion around Equation (6)), another prerequisite for a time-dependent perturbative approach is a slow and fast time-varying factorized time profile for the field, the slow factor being the field’s envelope and the fast factor oscillating with the carrier-envelope frequency,
 (11)
(11)The condition for slow and fast variation is mathematically expressed by
To demonstrate in what way the TDSEs are simplified we apply a perturbative treatment in the ionization scheme depicted in Figure 2(a). One can have as its starting point the EOMs of Equation (8) and develop a time-dependent perturbation resonant ionization theory by isolating the equations for the ground state
 (12a)
(12a) (12b)
(12b) (12c)
(12c) (12d)
(12d) (12e)
(12e)In these equations,
 (13)
(13)Note that at this level of approximation, further transitions from the AIS to higher continuum states are not included because they are expected to only become significant at higher intensities. One therefore succeeds in reducing a highly demanding computational problem to a very manageable set of equations which, it is worth noting, is expressed through experimentally measured quantities (energies, shifts, q-parameters, widths). Following the solutions of the perturbative EOMs one may calculate the ionization yield as
 (14)
(14)![]()
Figure 6.Ionization of lithium with a radiation field around 73.1 eV ( H47) couples two AIS states. The lower state decays to Li
H47) couples two AIS states. The lower state decays to Li whereas the higher state decays to Li
whereas the higher state decays to Li .
.
The lithium in its ground state
This is a particularly interesting scheme because the resonant coupling between the ground state,
It is also worth exploring the effects of Rabi coupling between the AIS on the ionization yield. As autoionization via the AISs competes with direct photoionization it is expected that the pulse duration relative to the half-life of the AISs plays a role here. These lifetimes are approximately
![]()
Figure 7.Ionization of lithium with a radiation field around 73.1 eV ( H47) coupling two AIS states. We plot the population ratios of Li
H47) coupling two AIS states. We plot the population ratios of Li /Li
/Li for various coupling strengths of
for various coupling strengths of  and for peak intensity
and for peak intensity  W/cm
W/cm . The multiplication factor for the
. The multiplication factor for the  coupling is shown in the inset. Values for
coupling is shown in the inset. Values for  and
and  can be found in Ref. [48].
can be found in Ref. [48].
6 Conclusions
The high intensities, achieved recently, in both FEL and laser-driven attosecond facilities, in the XUV spectral region opened up the era of strong field effects in this short-wavelength part of the electromagnetic radiation spectrum. In this work, we addressed near-future perspectives of investigations in this area. Several effects, well found in the visible spectral regime, are extendable to the XUV range under the experimental conditions that exist today. Examples of such experiments, enabling control of processes and dynamics during the interaction of the radiation with matter as well as modifying the propagation properties of the XUV radiation in matter have been presented. Ab initio numerical modeling of some of these effects has demonstrated the observability of the effects at hand. At the same time, experimental obstacles and potential artifacts along with mitigation strategies have been elaborated. It is expected that the presented perspectives will motivate numerous near-future experimental campaigns in FEL and attosecond infrastructures.
References
[1] M. Ferray, A. L’huillier, X. F. Li, L. A. Lompre, G. Mainfray, C. Manus. J. Phys. B At. Mol. Opt. Phys., 21(1988).
[2] P. Agostini, F. Fabre, G. Mainfray, G. Petite, N. K. Rahman. Phys. Rev. Lett., 42, 1127(1979).
[3] L. V. Keldysh. Soviet Phys. JETP, 20, 1307(1965).
[4] L. V. Keldysh. Phys. Rev. Lett., 16, 1054(1966).
[5] C. Ott, L. Aufleger, T. Ding, M. Rebholz, A. Magunia, M. Hartmann, V. Stooß, D. Wachs, P. Birk, G. D. Borisova, K. Meyer, P. Rupprecht, C. D. C. Castanheira, R. Moshammer, A. R. Attar, T. Gaumnitz, Z.-H. Loh, S. Düsterer, R. Treusch, J. Ullrich, Y. Jiang, M. Meyer, P. Lambropoulos, T. Pfeifer. Phys. Rev. Lett., 123(2019).
[6] T. Ding, M. Rebholz, L. Aufleger, M. Hartmann, K. Meyer, V. Stooß, A. Magunia, D. Wachs, P. Birk, Y. Mi, G. D. Borisova, C. d. C. Castanheira, P. Rupprecht, Z.-H. Loh, A. R. Attar, T. Gaumnitz, S. Roling, M. Butz, H. Zacharias, S. Düsterer, R. Treusch, S. M. Cavaletto, C. Ott, T. Pfeifer. Phys. Rev. Lett., 123(2019).
[7] I. Orfanos, I. Makos, I. Liontos, E. Skantzakis, B. Major, A. Nayak, M. Dumergue, S. Kuehn, S. Kahaly, K. Varjú, G. Sansone, B. Witzel, C. Kalpouzos, L. A. A. Nikolopoulos, P. Tzallas, D. Charalambidis. J. Phys. Photon, 2(2020).
[8] A. Nayak, I. Orfanos, I. Makos, M. Dumergue, S. Kühn, E. Skantzakis, B. Bodi, K. Varjú, C. Kalpouzos, H. I. B. Banks, A. Emmanouilidou, D. Charalambidis, P. Tzallas. Phys. Rev. A, 98, 66(2018).
[9] I. Makos, I. Orfanos, A. Nayak, J. Peschel, B. Major, I. Liontos, E. Skantzakis, N. Papadakis, C. Kalpouzos, M. Dumergue, S. Kühn, K. Varju, P. Johnsson, A. L’huillier, P. Tzallas, D. Charalambidis. Sci. Rep., 10, 3759(2020).
[10] L. Jönsson. J. Opt. Soc. Am. B, 4, 1422(1987).
[11] C. J. G. J. Uiterwaal, D. Xenakis, D. Charalambidis, P. Maragakis, H. Schröder, P. Lambropoulos. Phys. Rev. A, 57, 392(1998).
[12] K.-J. Boller, A. Imamoğlu, S. E. Harris. Phys. Rev. Lett., 66, 2593(1991).
[13] O. A. Kocharovskaya, Y. I. Khani. Sov. Phys. JETP, 63, 945(1986).
[14] B. Dai, P. Lambropoulos. Phys. Rev. A, 39, 3704(1989).
[15] P. E. Coleman, P. L. Knight, K. Burnett. Opt. Commun., 42, 171(1982).
[16] Y. I. Geller, A. K. Popov. Sov. J. Quantum Electron., 6, 883(1976).
[17] Y. I. Geller, A. K. Popov. Sov. J. Quantum Electron., 6, 606(1976).
[18] S. Cavalieri, R. Eramo, L. Fini, M. Materazzi, O. Faucher, D. Charalambidis. Phys. Rev. A, 57, 2915(1998).
[19] S. Cavalieri, F. S. Pavone, M. Matera. Phys. Rev. Lett, 67, 3673(1991).
[20] Y. L. Shao, D. Charalambidis, C. Fotakis, J. Zhang, P. Lambropoulos. Phys. Rev. Lett, 67, 3669(1991).
[21] S. S. Dimov, L. I. Pavlov, K. V. Stamenov, Y. I. Heller, A. K. Popov. Appl. Phys. B, 30, 35(1983).
[22] Y. I. Heller, V. F. Lukinykh, A. K. Popov, V. V. Slabko. Phys. Lett. A, 82, 4(1981).
[23] O. Faucher, E. Hertz, B. Lavorel, R. Chaux, T. Dreier, H. Berger, D. Charalambidis. J. Phys. B, 32, 4485(1999).
[24] B. W. Shore, D. Charalambidis, M. Shapiro, P. L. Knight, T. Halfmann, K. Bergmann, L. P. Yatsenko, O. Faucher, S. Cavalieri, P. Lambropoulos. Phys. Rev. Lett., 93(2004).
[25] U. Fano. Phys. Rev., 124, 1866(1961).
[26] O. Faucher, D. Charalambidis, C. Fotakis, J. Zhang, P. Lambropoulos. Phys. Rev. Lett., 70, 3004(1993).
[27] L. Lipsky, A. Russek. Phys. Rev., 142, 59(1966).
[28] N. E. Karapanagioti, O. Faucher, Y. L. Shao, D. Charalambidis, H. Bachau, E. Cormier. Phys. Rev. Lett., 74, 2431(1995).
[29] L. A. A. Nikolopoulos, T. J. Kelly, J. T. Costello. Phys. Rev. A, 84(2011).
[30] N. Rohringer, R. Santra. Phys. Rev. A, 77(2008).
[31] M. Di Fraia, O. Plekan, C. Callegari, K. C. Prince, L. Giannessi, E. Allaria, L. Badano, G. de Ninno, M. Trovò, B. Diviacco, D. Gauthier, N. Mirian, G. Penco, P. R. Ribivc, S. Spampinati, C. Spezzani, G. Gaio, Y. Orimo, O. Tugs, T. Sato, K. L. Ishikawa, P.A. Carpeggiani, T. Csizmadia, M. Füle, G. Sansone, P. Kumar Maroju, A. D’Elia, T. Mazza, M. Meyer, E. V. Gryzlova, A. N. Grum-Grzhimailo, D. You, K. Ueda. Phys. Rev. Lett., 123(2019).
[32] K. C. Prince, E. Allaria, C. Callegari, R. Cucini, G. de Ninno, S. Di Mitri, B. Diviacco, E. Ferrari, P. Finetti, D. Gauthier, L. Giannessi, N. Mahne, G. Penco, O. Plekan, L. Raimondi, P. Rebernik, E. Roussel, C. Svetina, M. Trovò, M. Zangrando, M. Negro, P. Carpeggiani, M. Reduzzi, G. Sansone, A.N. Grum-Grzhimailo, E. V. Gryzlova, S. I. Strakhova, K. Bartschat, N. Douguet, J. Venzke, D. Iablonskyi, Y. Kumagai, T. Takanashi, K. Ueda, A. Fischer, M. Coreno, F. Stienkemeier, Y. Ovcharenko, T. Mazza, M. Meyer. Nat. Photon., 10, 176(2016).
[33] H. J. Shin, D. G. Lee, Y. H. Cha, J.-H. Kim, K. H. Hong, C. H. Nam. Phys. Rev. A, 63(2001).
[34] H. J. Shin, D. G. Lee, Y. H. Cha, K. H. Hong, C. H. Nam. Phys. Rev. Lett., 83, 2544(1999).
[35] C. Altucci, T. Starczewski, E. Mevel, C.-G. Wahlström, B. Carré, A. L’Huillier. J. Opt. Soc. Am. B, 13, 148(1996).
[36] E. Constant, D. Garzella, P. Breger, E. Mével, C. Dorrer, C. Le Blanc, F. Salin, P. Agostini. Phys. Rev. Lett., 82, 1668(1999).
[37] P. Tzallas, E. Skantzakis, L. A. A. Nikolopoulos, G. D. Tsakiris, D. Charalambidis. Nature Phys., 7, 781(2011).
[38] P. K. Maroju, C. Grazioli, M. Di Fraia, M. Moioli, D. Ertel, H. Ahmadi, O. Plekan, P. Finetti, E. Allaria, L. Giannessi, G. de Ninno, C. Spezzani, G. Penco, S. Spampinati, A. Demidovich, M. B. Danailov, R. Borghes, G. Kourousias, Dos Reis C. E. Sanches, F. Billé, A. A. Lutman, R. J. Squibb, R. Feifel, P. Carpeggiani, M. Reduzzi, T. Mazza, M Meyer, S. Bengtsson, N. Ibrakovic, E. R. Simpson, J. Mauritsson, T. Csizmadia, M. Dumergue, S. Kühn, H. Nandiga Gopalakrishna, D. You, K. Ueda, M. Labeye, J. E. Bækhoj, K. J. Schafer, E. V. Gryzlova, A. N. Grum-Grzhimailo, K. C. Prince, C. Callegari, G. Sansone. Nature, 578, 386(2020).
[39] N. A. Papadogiannis, L. A. A. Nikolopoulos, D. Charalambidis, G. D. Tsakiris, P. Tzallas, K. Witte. Appl. Phys. B, 76, 721(2003).
[40] H. Bachau, E. Cormier, P. Decleva, J. E. Hansen, F. Martín, Rep. Prog. Phys., 64, 1815(2001).
[41] E. Foumouo, A. Hamido, P. H. Antoine, B. Piraux, H. Bachau, R. Shakeshaft. J. Phys. B, 43(2010).
[42] P. Lambropoulos, L. A. A. Nikolopoulos. New J. Phys., 10(2008).
[43] L. A. A. Nikolopoulos, T. Nakajima, P. Lambropoulos. Phys. Rev. Lett., 90(2003).
[44] L. A. A. Nikolopoulos, T. K. Kjeldsen, L. B. Madsen. Phys. Rev. A, 75(2007).
[45] B. W. Shore. The Theory of Coherent Atomic Excitation(1990).
[46] P. Lambropoulos, P. Zoller. Phys. Rev. A, 24, 379(1981).
[47] K. T. Chung, B.-C. Gou. Phys. Rev. A, 52, 3669(1995).
[48] D. Middleton. The development of a theoretical and computational framework of ultrafast processes of complex atomic systems in a strong radiation field,(2014).
[49] D. Charalambidis, J. A. D. Stockdale, C. Fotakis. Z. Phys. D, 32, 191(1994).

Set citation alerts for the article
Please enter your email address



