Magnetic fields can directly affect the evolution of a fluid via the J × B force in the momentum equation. In a conducting fluid, the coupling is two-way, such that magnetic fields also follow the fluid motion. This leads to complex coupled magnetohydrodynamics (MHD) phenomena such as magnetic plasma confinement,1 MHD waves,2 magnetized fluid turbulence,3 accretion disk instabilities, and astrophysical jets.4

Electromagnetic plasma physics effects can arise even in initially unmagnetized plasmas. This is because self-generated magnetic fields arise through the Biermann mechanism, occurring around misaligned electron pressure and density gradients.5 Self-generated magnetic fields are therefore inherently linked to plasma asymmetries and vorticity generation. However, these self-generated fields are often neglected in modeling of high-energy-density (HED) plasmas. This is usually justified by arguing that the resulting J × B force is small compared with hydrodynamic pressure forces.

In this work, we argue that it is often incorrect to neglect these self-generated magnetic fields in HED plasmas. We show that in a hot enough plasma, the fields can become strong enough to indirectly affect hydrodynamics via localizing electrons and thereby insulating the electron heat flux.6 The magnetized reduction and deflection of heat flux then affects the hydrodynamics. The Biermann fields are especially potent, since they naturally arise around temperature gradients, precisely where heat flux is important. This feedback to hydrodynamics via the heat flux is of central importance to HED plasmas. Magnetized heat flux can lead to significant changes to hydrodynamics, temperature profiles, and drive symmetry.7,8 It can also affect growth rates of fluid instabilities, such as the ablative Rayleigh–Taylor instability.9 However, it is only covered under the Braginskii extended magnetohydrodynamics (XMHD) framework and is not a part of ideal MHD or resistive MHD. We provide a detailed discussion of XMHD effects and estimate their magnitude. By making some assumptions, their relative importance can be visualized across the two-dimensional density–temperature parameter space.

Owing to the strongly temperature-dependent nature of magnetic and heat flux effects, we find that XMHD can significantly affect hydrodynamics in hotter HED plasmas such as hohlraums,7 laser ablation fronts,10,11 Z-pinches, and inertial confinement fusion (ICF) fuel.12 We show that in the relevant regions of parameter space, XMHD reduces to the simpler resistive MHD and Hall MHD models. By making some further assumptions, it is possible to estimate the minimum temperature at which the self-magnetization saturates at a level strong enough to affect hydrodynamics.

Another important aspect is the magnetization of fast ion transport. Unlike the collision frequency, the magnetic gyrofrequency is independent of particle velocity (for nonrelativistic particles). This makes magnetic effects especially important for fast particles. For example, 3.5 MeV alpha particles from deuterium–tritium fusion reactions have a gyroradius of 27|B|⁻¹ cm, with B in tesla. Magnetic fields can reach levels where the fusion products are confined, affecting the fuel energy balance. This effect is used advantageously in magnetized ICF concepts. Furthermore, owing to the rapidly increasing temperature, self-generated magnetic fields are likely to affect burn wave propagation and ignition yield even in standard ICF.13

In Sec. II, we assess the theory of magnetized heat conduction, with reference to the density–temperature parameter space. In Sec. III, we describe the extension to the MHD theory of magnetic field advection. In Sec. IV, we compare terms in the induction equation to estimate the saturated self-generated magnetic field. Section V presents a summary and discussion.

There is a dimensionless parameter that indicates the importance of magnetic field in the fluid momentum (first fluid moment) equation. This is given byβ=2Pc2ϵ0|B|2≃0.25Pbar|B|T−2,(1)where P is the total (ion plus electron) internal plasma pressure, c is the speed of light, and ϵ₀ is the vacuum permittivity. Equation (1) does not consider the kinetic energy of the fluid. Therefore, for fluids with large Mach number, it may be pertinent to instead use the ram pressure betaβR=2ρ|u|2c2ϵ0|B|2≃2500ρgcm−3|u|kms−12|B|T−2(2)as a better measure of the relative importance of magnetic forcing. This expression contains the fluid mass density ρ and velocity u.

The magnetic field contributes to the effective pressure that forces the fluid. The J × B force also has a component related to the curvature of magnetic field lines. This tends to force the fluid in a direction that straightens the field lines. For example, with the interface curvature introduced by the Rayleigh–Taylor and Kelvin–Helmholtz instabilities, the magnetic tension can stabilize the interface.14 However, the magnetic pressure and tension effects are only measurable14 when β + β_R < 100.

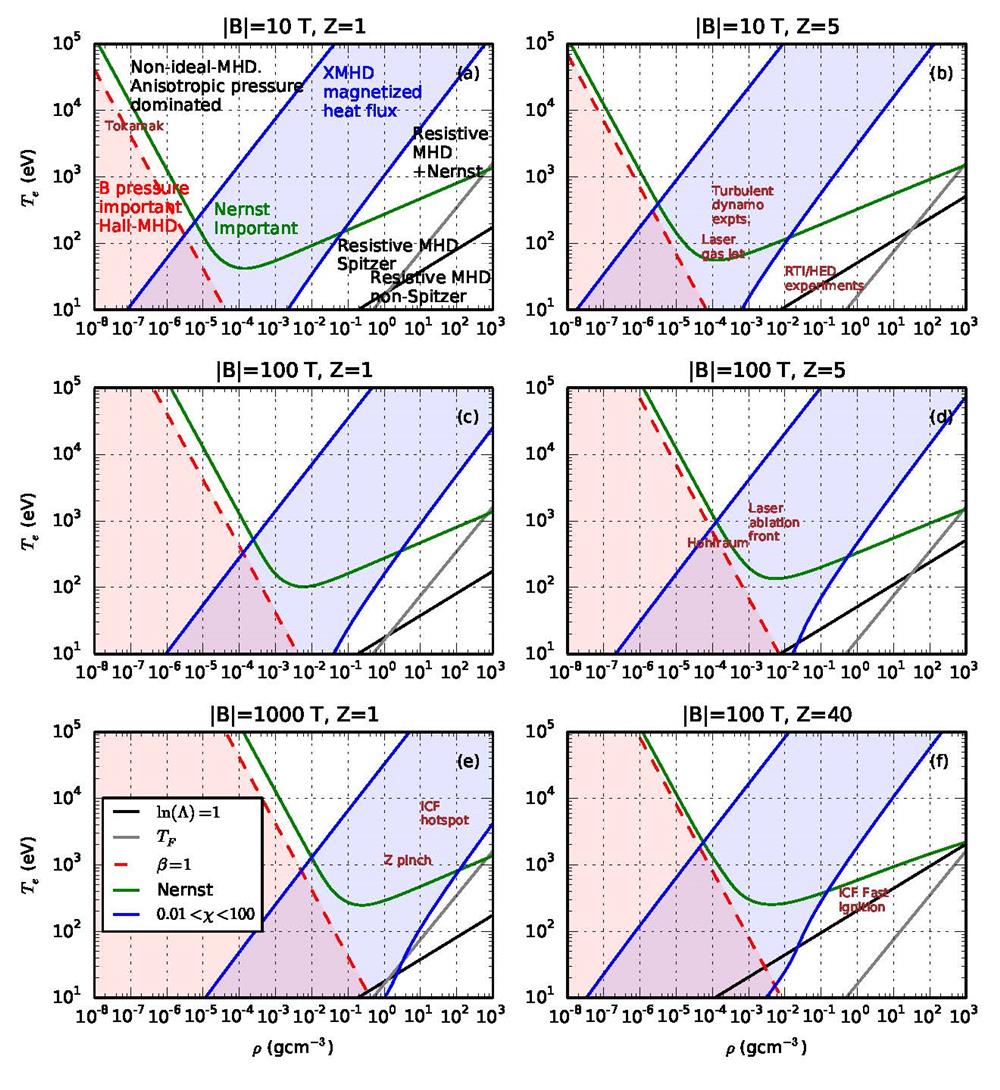
The region β < 1 is visualized in red in the parameter space in Fig. 1. Since this plot neglects the contribution of β_R, it is valid only for Mach numbers much less than one. Figure 1(a) shows the case for a typical laboratory field strength of 10 T. Tokamak fusion plasmas have β ≃ 1, as required for efficient use of the available magnetic field strength. Other panels in Fig. 1 show the alterations due to increased field strength or ionization Z. It should be noted that all figures in this work assume an ion charge-to-mass ratio Z/A = 1/2, where A is the ion mass number.

Figures 1(c)–1(f) are for higher magnetic field strengths, as can be achieved by plasma compression. Self-generated fields in laser-produced plasmas can also reach 100 T.15 Parameters measured for several different experiments are highlighted on the plots. It is clear that initially unmagnetized HED plasmas often have β ≫ 1, typically β ≃ 100 or more. We note that this conclusion is strengthened by the inclusion of β_R and the fluid kinetic energy. With β ≫ 1, it is often assumed that self-generated magnetic fields have no effect on the plasma and so fluid evolution is described by pure hydrodynamics. However, this is not necessarily true. This is because magnetic fields can still affect the hydrodynamics system closure through higher-order fluid moments such as the magnetized heat flux. These transport processes depend on the relative importance of plasma Coulomb collisions and magnetic fields, given by the electron Hall parameter16χ=e|B|τme≃6.1×1016Z⁡lnΛTeeV3/2|B|Tnecm−3−1,(3)where Z is the ion charge state, ln Λ is the Coulomb logarithm, and n_e, T_e, e, m_e, and τ are the electron number density, temperature, charge, mass and Braginskii electron–ion Coulomb collision time, respectively. The Hall parameter indicates the strength of electron magnetic gyromotion in comparison with Coulomb collisions. The regions with 0.01 < χ < 100 are indicated in blue in the parameter space in Fig. 1. It should be noted that the curves in all figures of this work are plotted using numerical solutions. This is necessary because the Coulomb logarithm also depends indirectly on T_e.

Astrophysical plasmas have wide ranges of plasma β and electron Hall parameter χ. XMHD effects are likely to be important in protoplanetary disks17 and possibly in the early universe.18 For most other astrophysical and space systems, while the plasma β can range from ≪1 (e.g., in pulsars and astrophysical jets) to ≫1 (e.g., in galaxy clusters and the dense parts of accretion disks), χ tends to be much larger than unity. For example, the solar wind has density n_e ≃ 10 cm⁻³, temperature 100 eV, and |B| ≃ 10⁻⁴ T. This results in χ ≃ 10¹³.

Conversely, if χ ≪ 1, magnetic fields are unimportant for transport processes. The electrons are primarily confined by Coulomb collisions. This means that the unmagnetized Spitzer heat flux fluid closure is applicable. This results from faster electrons in the tail of the distribution function moving down the temperature gradient. The central idea of XMHD is that the electron collisions and magnetic gyromotion may be on similar timescales, such that χ ≃ 1. The paths of the faster electrons are then bent by their gyromotion. This effectively confines the electron motion perpendicular to the field and therefore reduces the heat conductivity below the Spitzer value. The heat conductivity becomes anisotropic because electron motion and conductivity along the field line are unaffected.

As can be seen in Fig. 1, HED plasmas are often characterized by this intermediate regime 0.01 < χ < 100 (shown in blue) with the magnetized heat flux. This includes laser plasma experiments,19 turbulent dynamo experiments,4,20 magnetized ICF,21 hohlraums,7 magnetized liner inertial fusion22 and Z-pinches.

The transport processes are heavily dependent on Z [Eq. (3)]. Therefore, we present copies of the parameter space for various values of Z. Figure 1 also shows panels for various magnetic field strengths. For example, high-power near-visible lasers have a critical density around 10⁻³ g cm⁻³ and are often intense enough to produce temperatures >100 eV at the ablation front. Figure 1(d) shows that self-generated field strengths of ≃100 T are enough to magnetize the electron heat flux and change the ablation process.23,24 This means that the full Braginskii XMHD model is required to properly describe the heat flux, and the Spitzer model is invalid. Furthermore, these heat flux models are only valid in the weakly coupled plasma and nondegenerate regions above the gray and black lines in Fig. 1. The meaning of the green curves in Fig. 1 will be discussed in Sec. III.

The hot electrons that carry the heat flux are confined and deflected by the Lorentz force −e(v_e × B), where v_e ∝ −∇T_e is the velocity of hot electrons down the temperature gradient. This intuitive argument leads us to expect that the heat flux is deflected in the direction of ∇T_e × B by the magnetic field. Kinetic theory indicates that this is indeed true. For example, in the special case where the magnetic field direction b^=B/|B| is perpendicular to the temperature gradient and current, the full derivation results in the Braginskii electron heat fluxq=neTeτme(−κ⊥∇Te+κ∧∇Te×b^)+Tee(−β⊥J+β∧J×b^).(4)The full three-dimensional theory is of similar character, and is given in Refs. 6, 16, 25, and 26. The XMHD formulation relies on the precise kinetic interaction of magnetic gyromotion with Coulomb collisions. These transport properties are encapsulated in the positive dimensionless κ and β transport coefficients,6,16,25,27 depending only on χ and Z. They must be found from kinetic theory. Equation (4) shows that heat flux can also be carried by an electric current, with terms proportional to the β transport coefficients. We will show in Sec. IV that in HED plasmas, the temperature gradient terms usually dominate over these current terms.

The perpendicular (⊥) coefficients describe transport perpendicular to B, giving the heat flux for the component of −∇T_e or −J that is perpendicular to B. The cross-perpendicular (∧) coefficients describe the deflection of the heat flux by the magnetic field, into the direction of ∇Te×b^ or J×b^. The deflection becomes prominent (κ_∧ ≃ κ_⊥) when the field produces gyromotion of a similar strength to collisions, meaning χ ≃ 1. For example, even a Hall parameter as low as χ ≃ 0.01 is enough to change the heat flux profile and invert the asymmetries in a laser ablation front.24 These asymmetries act as a seed for Rayleigh–Taylor instability in ICF, and can have a large effect on overall fusion yield.

Kinetic theory gives κ_⊥(χ, Z) < κ_⊥(0, Z), in agreement with the intuitive argument that magnetic fields should insulate the perpendicular heat flux. In the case of χ = 0, the Spitzer theory is recovered. The Spitzer coefficient κ_⊥(0, Z) is often written as κ_∥(Z), because it also describes transport parallel to B, which is unaffected by the magnetization.

An additional consideration is that this magnetic insulation and deflection of heat flux will only be important if the heat flux itself is relevant. This can be measured via the hydrodynamic heat flux Péclet number, given by |u|L_T/D_T, where the Spitzer thermal diffusivity D_T ≃ T_eτ/m_e and L_T = T_e/|∇T_e|. This is a similar quantity to the Reynolds number, but it measures the importance of electron heat flux rather than viscosity. The Péclet number indicates that the heat flux becomes more important as the temperature is increased. If the Péclet number is much larger than 1, then energy flow is dominated by bulk flow, rather than by the heat flux.

The Spitzer and Braginskii heat flux models also require local transport. This means that electrons must be confined by Coulomb collisions or gyromotion to a region much smaller than the gradient scale-length of any fluid quantity. This condition can be invalidated for some of the experiments in Fig. 1. For example, the electron Coulomb mean free path can exceed L_T/10 in laser ablation fronts. Nonlocal models28,29 have been developed to more accurately describe the heat flux under these conditions. They are more computationally demanding than the local transport models, although they have had some success in reproducing fully kinetic simulations.30 Adding magnetization to these models has so far proved challenging.

To correctly predict magnetized heat conduction, the evolution of the magnetic field must be known. Collisions significantly change the advection of the magnetic field.6 It no longer simply advects with the fluid, as in ideal MHD. For example, magnetic fields were measured to accumulate near the target surface in a laser ablation front.15 However, ideal MHD predicts advection outward with the ablated plasma flow. Derivation of the electric field Ohm’s law from the kinetic Vlasov–Fokker–Planck equation and substitution into Faraday’s law explains this discrepancy. In a simplified two-dimensional x–y geometry, where the magnetic field B=Bz(x,y)z^ is out of the x–y plane, the result can be written as∂Bz∂t+∇⋅(uBBz)=∇⋅(D∇Bz)+|∇ne‖∇Te|sin⁡θnee,(5)where θ is the angle between ∇T_e and ∇n_e. This reduced two-dimensional formulation is adequate to assess the relative magnitude of different terms. Again, the full three-dimensional theory is of similar character, and is given in Refs. 6, 16, 25, and 26.

Equation (5) is a simple advection–diffusion equation, with a source term. Electron pressure creates the source term for self-generated magnetic fields. In the collisionless case, the electron pressure tensor can be highly anisotropic and produce Weibel magnetic filaments.31 However, the nature of the source term changes if Coulomb collisions confine electrons to a local region.31 This requires that the density, temperature and magnetic scale-lengths L_T = T_e/|∇T_e|, L_n = n_e/|∇n_e|, and L_B = |B_z|/|∇B_z| must greatly exceed the electron Coulomb mean free path. In this local transport description, the source term reduces to that given in Eq. (5), known as the Biermann battery. This means that misaligned density and temperature gradients will self-generate a magnetic field, even in an initially unmagnetized plasma. Gradients in ionization can also be a source of magnetic fields.32

The main effect of the Coulomb collisions is to create a resistance to currents. This causes diffusion of the magnetic field with diffusivityD=mec2ϵ0α∥(Z)nee2τ,(6)depending on the resistive transport coefficient α_∥(Z). This diffusion is included in the resistive-MHD description. However, XMHD also includes alterations to the magnetic advection velocityuB=u−(1+δ⊥)Jnee+δ∧J×b^nee−γ⊥τme∇Te+γ∧τme∇Te×b^.(7)In contrast with ideal MHD or resistive MHD, this is no longer just the fluid velocity u. Fluid flow, electric currents, and temperature gradients all act as a driver for magnetic field transport. These processes depend on the γ(χ, Z) and δ(χ, Z) transport coefficients. The transport of magnetic fields down a temperature gradient is known as Nernst advection. It is the term proportional to γ_⊥ in Eq. (7). This term is often significant in HED plasmas, and it can be comparable to the ideal advection.15 The γ_∧ cross-Nernst term describes the deflection of the Nernst advection, in the same way that the heat flux is deflected in Eq. (4). The Hall velocity −J/(n_ee) is also slightly enhanced and deflected by the terms containing δ_⊥ and δ_∧. However, in Sec. IV, we will see that the Nernst terms usually dominate over these current terms in HED plasmas. We note that the term containing δ_∧ produces a diffusion of magnetic field. It can instead be included in the diffusive term containing D, resulting in increased resistivity as the Hall parameter increases. However, the formulation used in Eq. (7) better elucidates the symmetry between magnetic field advection and the heat flux in Eq. (4).

The similarities between Eqs. (4) and (7) can be intuitively understood by considering the central idea of MHD, namely, that the magnetic field is frozen into the conducting fluid. The additional insight in XMHD is that the Coulomb collision frequency rapidly decreases with electron speed, so that the faster electrons constitute the most conductive part of the electron fluid. This means the magnetic field mainly travels with the faster electrons in the tail of the distribution function. For example, faster electrons travel down temperature gradients, carrying a heat flux. The magnetic field is frozen into this flow of fast electrons, and so it must simply travel with the heat flux. As discussed in Sec. II, if the Hall parameter is significant, the heat flux is deflected by the magnetic field. Owing to the frozen-in behavior, Nernst magnetic field advection must also be deflected.

Starting from the kinetic equation, Haines33 showed that this analogy is exact in the case of an artificial electron collision time τ ∝ v², where v is the electron speed. However, switching to the true Coulomb rate τ ∝ v³ does not change the physical intuition. We therefore expect magnetic fields to be advected approximately with the electron heat flux from Eq. (4). However, the analogy is now no longer exact and is only qualitative. This is why the γ and δ transport coefficients for magnetic field advection are slightly different to the κ and β ones for heat flux. However, numerical calculations from the kinetic equation16,27 show that κ and β have a similar functional form to the γ and δ coefficients, in keeping with the physical picture.

The effect of each term in Eqs. (5)–(7) is shown pictorially in Fig. 2. This presents the advection streamlines of a mock-up out-of-plane magnetic field, meant to emulate the Biermann fields that form around a laser ablation spot.15 The laser would be incident from positive x and strike a target at the origin. The ablation causes a temperature gradient and fluid velocity in the positive x direction. The electron temperature rises linearly from 1 to 2 keV between x = 0 and x = 0.25 mm. The electron pressure is uniform at n_eT_e = 32 Mbar, and the fluid velocity is uniform at 40 km s⁻¹ along x. The average ion charge state is set to Z = 5. All plots and estimates in this work have been calculated using the transport coefficient fit functions of Ref. 16.

The outward advection with the ion fluid velocity u in Fig. 2(a) is the result from ideal MHD. There is also the Hall advection in Eq. (7) with velocity −J/(n_ee). This corrects the advection such that the magnetic field moves with the electron fluid, rather than the ion fluid. This Hall velocity is slightly modified by the XMHD terms containing the δ coefficients. There is also the collisional Nernst term that advects magnetic fields down the temperature gradient.

As we have discussed, these collisional XMHD terms can be magnetized in the same way as the heat flux. Equation (7) shows that their magnitude is reduced and the direction is deflected.16 This is described by the variation of the δ_⊥, δ_∧, γ_⊥, and γ_∧ coefficients with χ. The δ_∧ term deflects the Hall streamlines into a spiral pattern in Fig. 2(b). The magnetization is more obvious for the Nernst streamlines, which are deflected away from the temperature gradient direction in Fig. 2(c). The heat flux streamlines are deflected by the magnetic field in a very similar way. This demonstrates the analogy between the transport of magnetic field and electron heat flux16,33 that was discussed previously. The Nernst speed is higher farther away from the target, where the plasma is hotter.

The resistive diffusion is shown in Fig. 2(d). Diffusion tends to reduce the peak field strength and smear out magnetic features. Figure 2(e) shows the total of all these effects. The relative magnitude of each term is dependent on the plasma conditions. In agreement with the laser experiment,15 the inward Nernst advection can exceed the outward ideal advection, causing compression of magnetic field into the overdense conduction zone. Since the Nernst term can be inhibited by magnetization, but the ideal advection is unaffected, the result is a complex behavior where the advection direction is reversed in some magnetized regions. It was recently found that the transport coefficient fit functions must be carefully formulated.16,27 Previous approximations to kinetic simulations25 do not accurately reproduce the behavior in Fig. 2 and can cause discontinuous advection.

To visualize the relative importance of each of these induction terms in the parameter space in Fig. 1, it is informative to take their ratios. To reduce these ratios to a form that can be visualized, it is necessary to assume that L_T ≃ L_n ≃ L_B. Making this assumption, the ratio of the Biermann (electron pressure) term to the Hall term is n_eT_e/(c²ϵ₀|B|²). Although this does not include the ion pressure, it is approximately equal to the total plasma β in Eq. (1). We therefore see that in the β ≪ 1 red region in Fig. 1, the electron pressure term can be neglected in the induction equation. Conversely, β ≫ 1 implies that electron pressure and self-generated magnetic fields are important, but the magnetic field has little effect back on the fluid momentum equation, since |J × B| ≪ |∇P|.

Again considering Eqs. (5)–(7) and taking L_T ≃ L_n ≃ L_B, the ratio of the Hall advection term to the resistive diffusion term is approximately χ. We therefore see that above the blue region in Fig. 1, resistive diffusion is small compared with Hall advection. In the limit β ≪ 1 and χ ≫ 1 the resistive and pressure terms are negligible and the δ and γ transport coefficients go to zero, meaning we are left with u_B = u − J/(n_ee), known as Hall MHD. This is valid in the red region.

In the opposite limit of χ ≪ 1, the Hall terms are negligible compared with the resistive diffusion, a regime known as resistive MHD. The dominant terms are then the ideal advection u and the resistive diffusion. The ratio between these is the magnetic Reynolds number R_M = |u|L_B/D. This gives an indication of the relative importance of magnetic advection and diffusion. In HED plasmas, the J × B forces are often comparable to viscous forces. This can affect MHD turbulence properties.34 However, the magnetized transport effect can be much stronger than either, affecting the large-scale evolution of the temperature profile.

The χ ≪ 1 resistive diffusion regime is further subdivided into a part where plasma Spitzer resistivity is valid (for ln Λ ≫ 1) and a part where a tabulated material resistivity must be used. In resistive MHD, the Biermann and Nernst advection terms must also be retained. We note that the Nernst term is often incorrectly neglected in resistive-MHD modeling of HED plasmas. For example, the ratio of the Nernst term to the resistive diffusion term in Eqs. (5)–(7) isγ⊥τTeBzmeL2nee2τL2mec2ϵ0α∥Bz=γ⊥α∥neTee2τ2me2c2ϵ0≃4Temec2ΛlnΛ2γ⊥(χ,Z)α∥(Z).(8)This is directly related to how weakly coupled the plasma is. The region where this ratio exceeds 1 is shown in green in Fig. 1. The transport coefficients use the fit functions of Ref. 16.

The Nernst advection is more important in hotter, weakly coupled plasmas. Some HED plasmas, such as hohlraums and the solar core, fall in this regime, such that Nernst advection is at least as important as resistive diffusion. Nernst advection often dissipates the magnetic field, since it advects toward colder and more resistive regions. Standard resistive MHD is therefore unlikely to capture all of the relevant magnetic field evolution. By contrast, the Nernst effect can be neglected for colder HED plasma experiments below the green line in Fig. 1. This includes, for example, the Rayleigh–Taylor instability in cylinder implosions35,36 [“RTI/HED” experiments in Fig. 1(b)].

In the panels for higher field strength in Fig. 1, the red and blue regions shift toward higher plasma density, whereas the green separatrix for the Nernst-dominated regime is almost unchanged in the region with χ < 1. For example, the fuel hot-spot in ICF is also within the Nernst-dominated regime. It is also within the blue region where magnetized heat flux will impact hydrodynamics. Self-generated magnetic fields slightly enhance fusion yield by insulating the hot-spot,12 but they can also negatively impact the shape of the hot-spot and the growth of instabilities.12

In conclusion, the Hall parameter χ indicates the transition from resistive MHD (χ ≪ 1) to the weakly collisional MHD model at χ ≫ 1. In the intermediate regime χ ≃ 1, collisions are of similar importance to magnetic gyromotion, meaning the full transport coefficients, magnetized heat flux, and XMHD model must be calculated. For χ ≪ 1, the resistive-MHD and Spitzer heat flux models are sufficient. However, Nernst advection of the magnetic field may still be significant.

To further elaborate on the self-magnetization, Fig. 3 shows several cuts through parameter space at fixed plasma density. The upper panels have fixed magnetic field strength and the lower panels have fixed temperature. Conditions have been chosen to represent self-generated magnetic fields in HED shock tube experiments36 (left panels), laser ablation fronts (center panels) and compressed inertial confinement fusion hot-spots (right panels). As in Fig. 1, we assume L_T = L_n = L_B, each with a value of L = 20 µm. However, with the exception of ideal advection, all terms are ∝L⁻², and so changing L does not change their relative magnitudes.

Considering the dotted lines in Figs. 3(a)–3(c), the Coulomb logarithm is in the range 1–10 for these HED conditions. We have used the form 0.5 + 0.5 ln(1 + Λ²), whereΛ=e23TeeV3/2necm−3−1/2Z−1.(9)To plot the ideal advection, we must assume a value for the fluid velocity. We have taken a value equal to the sound speed, and so the ideal term (blue) is dominant in most panels. In subsonic or stagnated plasmas, the ideal advection will not be as important as Fig. 3 suggests. The Nernst advection (green) is also a dominant term, especially at higher temperatures. Depending on the plasma profiles, these advection terms can enhance or dissipate the magnetic field.

The Hall advection (red) is usually negligible for HED plasmas. The diffusion term (gray) decreases with temperature. The dashed line shows the Hall parameter χ, increasing with temperature. This does not become significant for the shock tube experiments, whereas it can exceed 1 and magnetize the heat flux in the hotter laser or fusion plasmas.

The lower panels show the dependence on magnetic field strength. The Biermann source term (purple) is independent of the field strength, and so the self-generated field will continue to grow from zero until other terms become comparable to it. Figures 3(d)–3(f) therefore allow us to find an estimate of the equilibrium self-generated field strength by finding the intersection of the source term (purple) with the most dominant dissipation term. In the shock tube experiments at T ≃ 50 eV, Nernst and Hall advection are both negligible.37 The evolution is mostly dominated by the ideal and resistive terms, or resistive MHD. If flow is significantly subsonic, the resistive diffusion is the dominant term. It causes saturation when it equals the Biermann source term (intersection of purple and gray lines) at around |B| ≃ 10 T. This results in χ ≃ 0.001 (dashed line), and so the heat flux is not magnetized.

By contrast, the hotter laser ablation plasma in Fig. 3(e) can have Nernst advection exceeding ideal advection, even with supersonic flow. The ideal and Nernst advection are in opposite directions (Fig. 2), and so there is a spatial position where they cancel out, with field strength given by the intersection of the green and blue lines. This point has |B| ≃ 100 T and χ ≃ 1. Laser ablation therefore requires the full XMHD treatment with magnetized heat flux. This magnetization effect can also be seen in Fig. 3(e), where the Nernst term tails off for χ > 1. There is a similar reduction in the electron heat flux.

In Fig. 3(f), the magnetic advection in ICF fuel is dominated by the ideal and Nernst terms. Which one is larger depends on the Mach number, or the level of residual kinetic energy at fuel stagnation. Resistive diffusion and Hall advection are generally quite small in the hot-spot, although resistance will become important if the field is Nernst-advected into the colder hydrogen shell, as seen in Fig. 3(c). In a well-stagnated hot-spot, the fuel flow is very subsonic, and so the ideal advection (blue) will not saturate the Biermann growth. Given the flow convergence, the ideal advection can even enhance the magnetic fields. Given enough time to grow, the self-generated magnetic field will therefore not saturate until it is balanced by Nernst advection at |B| ≃ 10³ T and χ ≃ 0.1, meaning that heat flux magnetization must be considered in the hot-spot.12

Of course, our assumption that L_T ≃ L_n ≃ L_B may not hold for realistic plasma profiles, meaning XMHD numerical simulations will be required. However, making this assumption has enabled estimates of the saturated self-generated magnetic field strength for several scenarios. This reduces the parameter space to just two dimensions (density and temperature). Below the green line in Fig. 1(a), the dominant saturation mechanism for the growing Biermann fields is resistive diffusion. Above the green line, the picture becomes more complicated, because the Nernst term becomes dominant. If the fluid flow is sufficiently fast, ideal advection may also play a part in causing saturation.38 Assuming that the Biermann term is balanced solely by resistive diffusion, and again assuming L_T ≃ L_n ≃ L_B, leads to∇⋅(D∇Bz)=|∇ne‖∇Te|sin⁡θnee,(10)Bmax≃0.012TeV5/2⁡sin⁡θα∥Z⁡lnΛ(T),(11)where T_eV is the electron temperature in eV. This estimate has been previously derived by Haines.38 We immediately see that the saturated field strength is heavily dependent on temperature. The estimated saturated field will also be stronger in lower-Z plasma.

To know if these saturated Biermann fields are strong enough to magnetize the heat flux, we must substitute into Eq. (3) to calculate the corresponding Hall parameterχmax=eBmaxτme≃1.2×10−9A⁡sin⁡θα∥Z3(lnΛ)2TeV4ρcc,(12)where A is the ion atomic mass number and ρ_cc is the mass density in g cm⁻³. This estimate has a strong dependence on electron temperature and ion charge state. It also increases with the angle between the electron density and temperature gradients. Maximizing this angle requires the introduction of strong multidimensional plasma asymmetries. The Biermann source term is zero in a one-dimensional or spherically symmetric geometry.

The minimum temperature required to reach χ ≃ 0.1 and magnetize the heat flux is shown in Fig. 4. Contours are shown for Z = 1 and Z = 5. We have assumed sin θ = 0.1, typical of the strong Biermann generation in a shear layer.39

The other terms in Eq. (5) may be important as well. In particular, above the green line in Fig. 1, Nernst advection dominates over the resistive diffusion. This is true even for χ ≪ 1. Depending on the exact temperature profile, Nernst advection can act to either increase or decrease |B|. However, it advects magnetic field toward colder regions, and so it often decreases the Hall parameter [Eq. (3)]. A similar balancing calculation, using the Nernst term, gives∇⋅Bmaxγ⊥τme∇Te=|∇ne‖∇Te|sin⁡θnee,(13)Bmax≃meγ⊥eτsin⁡θ,(14)χmax≃sin⁡θγ⊥.(15)

The transport coefficient γ_⊥ > 0.2 for low Hall parameter χ < 1, and so Nernst advection will begin to affect Biermann magnetic field growth well before it produces χ ≃ 1. Inclusion of Nernst advection is therefore a requirement for predicting Biermann heat flux magnetization. Resistive MHD is insufficient.

Note that these estimates have not considered the fluid advection of the magnetic field. If there is convergence ∇ · u < 0 and R_M ≫ 1, then the Hall parameter may be increased somewhat beyond these estimates. For example, ideal advection results in χ > 1 in convergence of ICF hot-spots12 or can lead to even faster growth under the turbulent dynamo process.20

In summary, we have discussed the effect of magnetic fields on heat transport in HED plasmas. The Spitzer heat flux can be magnetized, meaning it is reduced in magnitude and deflected. There is a qualitative symmetry between the flow of heat and the flow of magnetic field in the plasma. This leads to Nernst advection of magnetic field down temperature gradients. Owing to this symmetry with the heat flux, the Nernst advection of the magnetic field can itself be reduced and deflected when χ ≃ 1. We have discussed the parts of parameter space where the magnetization occurs and the full XMHD model must be used. In other parts of the parameter space, it reduces to resistive MHD or Hall MHD.

By taking line-outs in Fig. 3, we have also estimated the part of parameter space where self-magnetization could affect the hydrodynamics of HED plasmas. This requires Biermann self-generated fields from significantly misaligned density and temperature gradients. This XMHD effect reaches beyond the standard radiation hydrodynamic or ideal-MHD models. The magnetized heat flux effects have been modeled with the XMHD codes Gorgon12 and Hydra.7 XMHD capabilities are also being developed in Flash.27,39 The magnetized heat flux will affect the growth of fluid instabilities, heat confinement, and plasma symmetry.

Acknowledgment. The research presented in this article was supported by the Laboratory Directed Research and Development (LDRD) program of Los Alamos National Laboratory (LANL), under Center for Nonlinear Studies Project No. 20190496CR. This research was supported by LANL through its Center for Space and Earth Science (CSES). CSES is funded by LANL’s LDRD program under Project No. 20180475DR.