- Photonics Research
- Vol. 9, Issue 7, 1330 (2021)
Abstract
1. INTRODUCTION
The principle of coherent superposition of waves plays important roles in many well-known phenomena such as interference and diffraction. In quantum mechanics, the superposition principle, which is one of the fundamental nonclassical characteristics of quantum states, underlies many nonclassical properties of quantum mechanics including entanglement or coherence [1]. Recently, resource theories of coherence have attracted a lot of attention [2–4]. Quantum coherence, which characterizes the quantumness and underpins quantum correlations in quantum systems, plays a key role in many novel quantum phenomena and has been identified as a quantum resource for quantum information processing [5–9]. Quantum coherence also plays a strong role in biology systems [10], such as photosynthetic energy transport, the avian compass, and sense of smell.
To quantify coherence, Baumgratz
In practical quantum computation and quantum information, decoherence coming from the inevitable interaction between a quantum resource and the environment is a main obstacle [50]. Up to now, the decoherence of squeezing, entanglement, and quantum steering in the thermal noise channel has been experimentally demonstrated [51–55]. Toward the application of quantum coherence, it is necessary to investigate the evolution of quantum coherence in lossy and noisy environment [56,57]. Very recently, it has been shown that quantum coherence can be robust against noise theoretically [58] and quantum coherence of optical cat states can be robust against loss [59].
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
In this paper, we experimentally quantify quantum coherence of Gaussian states, for example, a squeezed state and a Gaussian EPR entangled state, by measuring their covariance matrices. Then we investigate quantum coherence of these Gaussian states through lossy and noisy channels. We show that quantum coherence of these Gaussian states is robust against loss in a lossy channel, which is similar to the case of squeezing and entanglement of a Gaussian state. The most interesting thing is that the quantum coherence of these Gaussian states is still robust in a noisy channel even if the squeezing and entanglement of the Gaussian state disappear. The presented results provide useful reference for applying quantum coherence of a Gaussian state in practical quantum information processing.
2. PRINCIPLE OF THE EXPERIMENT
As shown in Fig. 1(a), the quantum coherence of a Gaussian state is distributed through a Gaussian thermal noise channel, and the quantum coherence of the output state is measured. Here we consider two kinds of Gaussian channels: one is a lossy channel where only vacuum noise is involved, and the other is a noisy channel where the noise higher than vacuum noise exists. The squeezed state and the EPR entangled state, which are generated from a nondegenerate optical parametric amplifier (NOPA) as shown in Fig. 1(b), are used as two examples to investigate the quantum coherence of a Gaussian state in our experiment. The NOPA cavity is in a semimonolithic structure, which is composed by an a-cut type II potassium titanyl phosphate (KTP) crystal (), whose front surface is used as input mirror, and a concave mirror with curvature radius of 50 mm. The NOPA is operating in the case of deamplification, i.e., the relative phase between the signal and the pump light is locked to . The lossy channel is simulated by combination of a half-wave plate (HWP) and a polarization beam splitter (PBS), and the noisy channel is simulated by combination of an HWP, two PBSs, and an ancillary coherent beam carrying Gaussian noise.
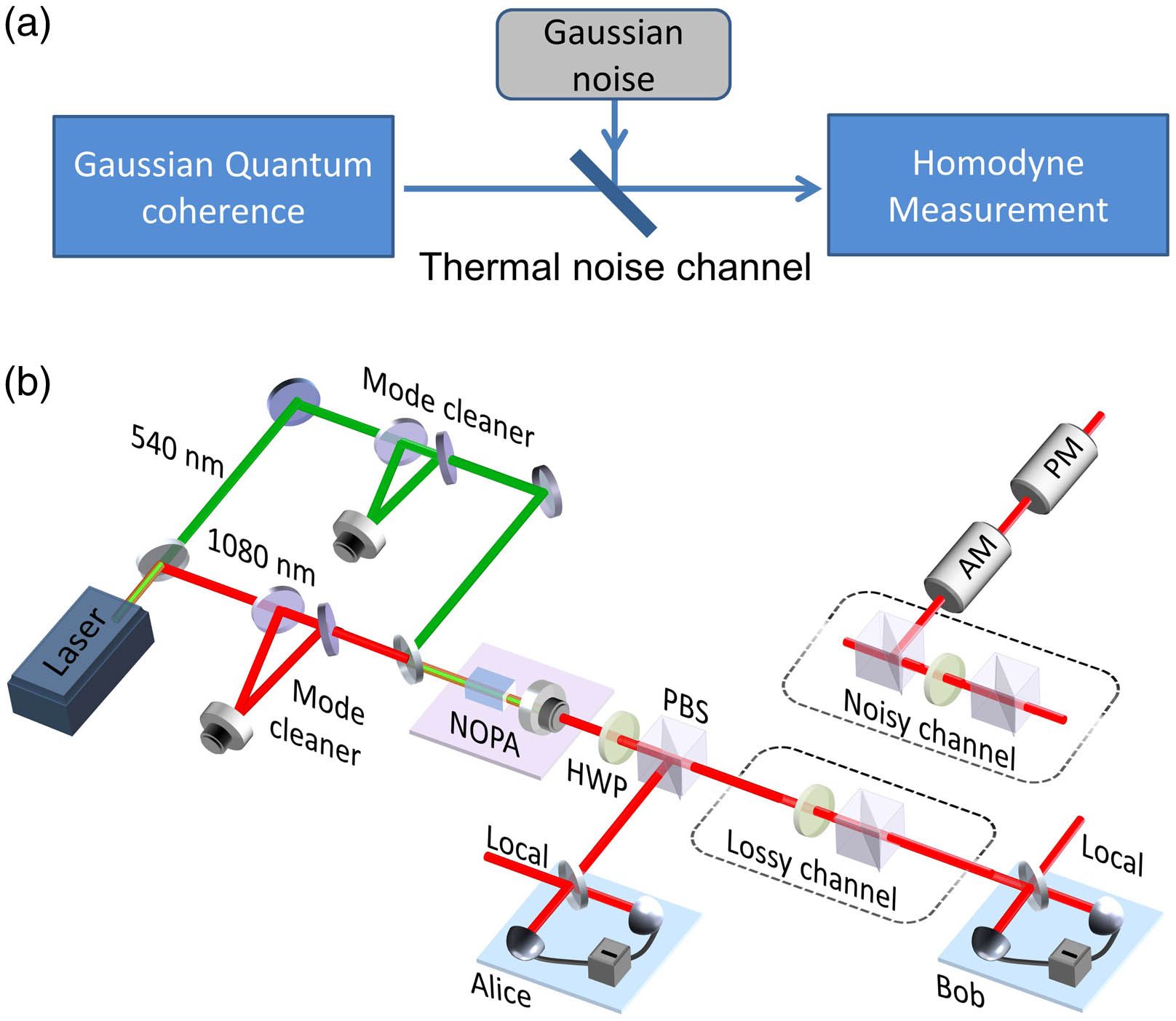
Figure 1.(a) Schematic of transmitting the quantum coherence of a Gaussian state in a thermal noise channel. (b) Experimental setup. The 1080 nm and the 540 nm laser outputs from the Nd:YAP/LBO laser pass through two mode cleaners and are injected into the NOPA as signal light and pump light, respectively. The output modes of the PBS behind the NOPA are an amplitude squeezed state (transmitted mode) and a phase squeezed state (reflected mode) or EPR entanglement state, when the HWP behind the NOPA is set to 22.5° or 0°, respectively. We use homodyne detectors to measure the output modes and a digital storage oscilloscope to record the experimental data. The interference efficiencies of homodyne detectors are 99%, and the quantum efficiencies of photodiodes (LASER COMPONENTS, InGaAs-PD-500um) are 99.6%. AM, amplitude modulator; PM, phase modulator.
At first, we distribute the amplitude squeezed state through a lossy channel, where the output state is measured by the homemade homodyne detector at Bob’s side in the time domain. Then we investigate the quantum coherence of an EPR entangled state in lossy channel, where output states are measured by Alice’s and Bob’s homodyne detectors simultaneously in the time domain. Finally, we quantify the quantum coherence of the amplitude squeezed state and EPR entangled state in a noisy channel, where the Gaussian noise is added through amplitude and phase modulators (LINOS, LM0202 P and LM0202 PHAS) on an ancillary coherent beam and coupled into the lossy channel by the PBS. In the measurement of the covariance matrix of output states in the time domain, the electrical signal of each homodyne detector is mixed with a 3 MHz reference signal (SRS, DS345), then passes through a low-pass filter and a low-noise preamplifier (SRS, SR560), and finally is recorded in a digital storage oscilloscope (Teledyne LeCroy, WaveRunner 640Zi). The bandwidth of the homodyne detectors we used is 8 MHz, and the common-mode rejection ratio is 30 dB (at 3 MHz). The sampling rate of the digital storage oscilloscope is 500 KS/s, and there are data for each sampling space.
3. QUANTUM COHERENCE
Quantum coherence of a quantum state in Fock space can be calculated by [1]
Since the displacements of the Gaussian states we used in our experiment are zero, the Gaussian state can be completely represented by its covariance matrix . The covariance matrix of the amplitude squeezed state is given by
The covariance matrix of the EPR entangled state is given by
A one-mode Gaussian state transmitting in a Gaussian channel can be represented by [61,62]
4. RESULTS
First we quantify the quantum coherence of the amplitude squeezed state and the EPR entangled state by the covariance matrices we reconstructed (see Appendix A) in a lossy environment. The decoherence of the squeezing of the squeezed state and the entanglement of the EPR entangled state in the lossy channel is shown in Figs. 2(a) and 2(b), respectively. It is obvious that the squeezing and entanglement are robust against loss in a lossy channel. Quantum coherence of the squeezed state and the EPR entangled state in a lossy channel is shown in Figs. 2(c) and 2(d), respectively. We can find that the quantum coherence of the squeezed state and the EPR entangled state is decreased with the increase of loss, which reaches zero only when the maximal loss is reached. When the loss equals 1, the squeezed state turns into a vacuum state and the EPR state turns into a separable state. We can see that the quantum coherence of these Gaussian states is also robust against loss in a lossy channel.
![]()
Figure 2.Experimental results in a lossy channel. (a) Dependence of squeezing (red solid line) and antisqueezing (blue dotted line) of the squeezed state on the loss. The dashed line is the shot noise limit (SNL). (b) Dependence of PPT value of the EPR entangled state on the loss. The dashed line is the boundary of the entangled and separable states. (c) and (d) Dependence of the quantum coherence of the squeezed state and the EPR entangled state on the loss, respectively. The initial squeezed and antisqueezed noise levels are −2.95 dB and 4.15 dB, respectively. The error bars represent one standard deviation and are obtained based on the statistics of the data.
Then we quantify the quantum coherence of a squeezed state and an EPR entangled state in a noisy environment. In the case of noisy channel, we fix the channel losses to and change the excess noise added on the amplitude squeezed state and one mode of the EPR entangled state. The decoherence of the squeezing of the squeezed state and the entanglement of the EPR entangled state in the noisy channel is shown in Figs. 3(a) and 3(b), respectively. Different from the results in the lossy channel, the noise level of squeezing is beyond the shot noise limit (SNL) when the excess noise over and the PPT value is greater than 1 when the excess noise is greater than , which means the squeezing of the squeezed state and the entanglement of the EPR entanglement state are destroyed.
![]()
Figure 3.Experimental results in a noisy channel. (a) Dependence of the squeezing (red solid line) and antisqueezing (blue dotted line) of the squeezed state on the excess noise. The dashed line is SNL. (b) Dependence of the PPT value of the EPR entangled state on the excess noise. The dashed line is the boundary of the entangled and separable states. (c) and (d) Dependence of the quantum coherence of the squeezed state and the EPR entangled state on the excess noise, respectively. (e) and (f) Quantum coherence of the squeezed state and the EPR entangled state parameterized by loss and excess noise, respectively. The red dots represent the experimental results in (c) and (d).
The quantum coherence of the squeezed state and the EPR entangled state in a noisy channel is shown in Figs. 3(c) and 3(d), respectively. It is obvious that the quantum coherence of the squeezed state and the EPR entangled state is decreased with the increase of the excess noises. However, the quantum coherence of these Gaussian states still exists even if the squeezing and entanglement disappear. It is interesting that the quantum coherence of these two Gaussian states will vanish only when infinite excess noises are involved in the case of fixed channel loss. The dependence of quantum coherence of the squeezed state and the EPR entangled state on loss and excess noise is shown in Figs. 3(e) and 3(f), respectively. It is obvious that the quantum coherence of these Gaussian states is robust against noise in a noisy channel.
We note that the squeezing and entanglement are destroyed at different excess noise levels as shown in Figs. 3(a) and 3(b). The reason for this result is that the excess noise is only added on one mode of the EPR entangled state. It shows that the EPR entanglement can tolerate more noise than the squeezed state in a one-mode noise channel. The squeezing and entanglement will be destroyed at same excess noise level if we add the excess noise on both modes of the EPR entangled state simultaneously (see Appendix B).
We also demonstrate the monotonicity of quantum coherences of the squeezed state and the entanglement state in lossy and noisy channels as shown in Figs. 2 and 3, respectively. The quantum coherences of these two Gaussian states are decreasing with the increase of loss and noise in quantum channels, which is because the lossy and noisy channels are all incoherent operations and quantum coherence will decrease under incoherent operations [1,47]. The physical reason for the robustness of quantum coherences of these Gaussian states in a noisy channel is that the proportion of quantum coherence is decreased when it is mixed with thermal noise, but the quantum coherence disappears completely only when infinite thermal noise is involved.
5. CONCLUSION
In summary, we experimentally demonstrate the quantum coherence of Gaussian states in lossy and noisy channels. The results confirm that the quantum coherences of the squeezed state and the EPR entangled state are robust against loss and noise in a Gaussian thermal noise channel, although the squeezing and entanglement of Gaussian states disappear at a certain noise level in a noisy channel. Thus, the quantum coherence of a Gaussian state can resist decoherence when it is used as quantum resource. Our investigation makes a step toward the application of quantum coherence as a quantum resource in quantum communication.
It is interesting to accomplish quantum information tasks that only require quantum coherence of a Gaussian state due to its unique property in the presence of loss and noise. However, a suitable application for only applying the quantum coherence of a Gaussian state remains an open question. Recently, it has been shown that the Gaussian entanglement can be transferred in a single-mode cavity [63], which is an application of robustness of quantum coherence of Gaussian states. Based on the presented results of robustness for quantum coherences of Gaussian states, the potential application of quantum coherence is worthy of further investigation.
APPENDIX A: RECONSTRUCTION OF THE COVARIANCE MATRIX
To reconstruct the covariance matrix of an EPR entangled state, the variances and the cross correlations of the amplitude or phase quadratures are obtained by simultaneously measuring the amplitude or phase quadratures of two modes of the EPR entangled state in the time domain. The diagonal elements of the covariance matrix are the variances of the amplitude and phase quadratures , and the nondiagonal elements are the covariances of the amplitude or phase quadratures, which are calculated via the measured variances [
APPENDIX B: TWO GAUSSIAN THERMAL NOISE CHANNELS
Here we consider the situation in which two modes of the Gaussian EPR entangled state are distributed through two Gaussian thermal noise channels, where the loss and excess noise are added on both modes of EPR entangled state as shown in Fig.?
![]()
Figure 4.Schematic of transmitting an EPR entangled state in two Gaussian thermal noise channels.
![]()
Figure 5.(a) and (b) Dependence of PPT values of the EPR entangled state on the loss and the excess noise, respectively. The dashed line is the boundary of the entangled and separable states. (c) and (d) Dependence of quantum coherence of the EPR entangled state on the loss and the excess noise, respectively. (e) Quantum coherence of the EPR entangled state parameterized by loss and excess noise.
The quantum coherences of the EPR entangled state in two lossy and noisy channels are shown in Figs.?
References
[1] T. Baumgratz, M. Cramer, M. B. Plenio. Quantifying coherence. Phys. Rev. Lett., 113, 140401(2014).
[2] A. Winter, D. Yang. Operational resource theory of coherence. Phys. Rev. Lett., 116, 120404(2016).
[3] A. Streltsov, G. Adesso, M. B. Plenio. Quantum coherence as a resource. Rev. Mod. Phys., 89, 041003(2017).
[4] E. Chitambar, G. Gour. Quantum resource theories. Rev. Mod. Phys., 91, 025001(2019).
[5] J. Åberg. Catalytic coherence. Phys. Rev. Lett., 113, 150402(2014).
[6] M. Hillery. Coherence as a resource in decision problems: the Deutsch-Jozsa algorithm and a variation. Phys. Rev. A, 93, 012111(2016).
[7] Y.-C. Li, H.-Q. Lin. Quantum coherence and quantum phase transitions. Sci. Rep., 6, 26365(2016).
[8] H.-L. Shi, S.-Y. Liu, X.-H. Wang, W.-L. Yang, Z.-Y. Yang, H. Fan. Coherence depletion in the Grover quantum search algorithm. Phys. Rev. A, 95, 032307(2017).
[9] Y.-H. Shi, H.-L. Shi, X.-H. Wang, M.-L. Hu, S.-Y. Liu, W.-L. Yang, H. Fan. Quantum coherence in a quantum heat engine. J. Phys. A, 53, 085301(2020).
[10] S. F. Huelga, M. B. Plenio. Vibrations, quanta and biology. Contemp. Phys., 54, 181-207(2013).
[11] X. N. Feng, L. F. Wei. Quantifying quantum coherence with quantum Fisher information. Sci. Rep., 7, 15492(2017).
[12] C. Yu. Quantum coherence via skew information and its polygamy. Phys. Rev. A, 95, 042337(2017).
[13] A. E. Rastegin. Quantum-coherence quantifiers based on the Tsallis relative
[14] C. Napoli, T. R. Bromley, M. Cianciaruso, M. Piani, N. Johnston, G. Adesso. Robustness of coherence: an operational and observable measure of quantum coherence. Phys. Rev. Lett., 116, 150502(2016).
[15] T. R. Bromley, M. Cianciaruso, G. Adesso. Frozen quantum coherence. Phys. Rev. Lett., 114, 210401(2015).
[16] E. Chitambar, A. Streltsov, S. Rana, M. N. Bera, G. Adesso, M. Lewenstein. Assisted distillation of quantum coherence. Phys. Rev. Lett., 116, 070402(2016).
[17] K. Bu, U. Singh, J. Wu. Catalytic coherence transformations. Phys. Rev. A, 93, 042326(2016).
[18] U. Singh, M. N. Bera, A. Misra, A. K. Pati. Erasing quantum coherence: an operational approach(2015).
[19] S. Cheng, M. J. W. Hall. Complementarity relations for quantum coherence. Phys. Rev. A, 92, 042101(2015).
[20] X. Yuan, G. Bai, T. Peng, X. Ma. Quantum uncertainty relation using coherence. Phys. Rev. A, 96, 032313(2017).
[21] Z. Xi, Y. Li, H. Fan. Quantum coherence and correlations in quantum system. Sci. Rep., 5, 10922(2015).
[22] E. Chitambar, M.-H. Hsieh. Relating the resource theories of entanglement and quantum coherence. Phys. Rev. Lett., 117, 020402(2016).
[23] Y. Yuan, Z. Hou, Y.-Y. Zhao, H.-S. Zhong, G.-Y. Xiang, C.-F. Li, G.-C. Guo. Experimental demonstration of wave-particle duality relation based on coherence measure. Opt. Express, 26, 004470(2018).
[24] K.-D. Wu, Z. Hou, H.-S. Zhong, Y. Yuan, G.-Y. Xiang, C.-F. Li, G.-C. Guo. Experimentally obtaining maximal coherence via assisted distillation process. Optica, 4, 454-459(2017).
[25] J. Gao, Z.-Q. Jiao, C.-Q. Hu, L.-F. Qiao, R.-J. Ren, H. Tang, Z.-H. Ma, S.-M. Fei, V. Vedral, X.-M. Jin. Experimental test of the relation between coherence and path information. Commun. Phys., 1, 89(2018).
[26] K.-D. Wu, Z. Hou, Y.-Y. Zhao, G.-Y. Xiang, C.-F. Li, G.-C. Guo, J. Ma, Q.-Y. He, J. Thompson, M. Gu. Experimental cyclic interconversion between coherence and quantum correlations. Phys. Rev. Lett., 121, 050401(2018).
[27] C. Zhang, T. R. Bromley, Y.-F. Huang, H. Cao, W.-M. Lv, B.-H. Liu, C.-F. Li, G.-C. Guo, M. Cianciaruso, G. Adesso. Demonstrating quantum coherence and metrology that is resilient to transversal noise. Phys. Rev. Lett., 123, 180504(2019).
[28] H. Xu, F. Xu, T. Theurer, D. Egloff, Z.-W. Liu, N. Yu, M. B. Plenio, L. Zhang. Experimental quantification of coherence of a tunable quantum detector. Phys. Rev. Lett., 125, 060404(2020).
[29] S. L. Braunstein, P. van Loock. Quantum information with continuous variables. Rev. Mod. Phys., 77, 513-577(2005).
[30] X.-B. Wang, T. Hiroshima, A. Tomita, M. Hayashi. Quantum information with Gaussian states. Phys. Rep., 448, 1-111(2007).
[31] C. Weedbrook, S. Pirandola, R. Garca-Patrón, N. J. Cerf, T. C. Ralph, J. H. Shapiro, S. Lloyd. Gaussian quantum information. Rev. Mod. Phys., 84, 621-669(2012).
[32] R. Ukai, N. Iwata, Y. Shimokawa, S. C. Armstrong, A. Politi, J.-I. Yoshikawa, P. van Loock, A. Furusawa. Demonstration of unconditional one-way quantum computations for continuous variables. Phys. Rev. Lett., 106, 240504(2011).
[33] X. Su, S. Hao, X. Deng, L. Ma, M. Wang, X. Jia, C. Xie, K. Peng. Gate sequence for continuous variable one-way quantum computation. Nat. Commun., 4, 2828(2013).
[34] X. Su, W. Wang, Y. Wang, X. Jia, C. Xie, K. Peng. Continuous variable quantum key distribution based on optical entangled states without signal modulation. Europhys. Lett., 87, 20005(2009).
[35] T. Gehring, V. Händchen, J. Duhme, F. Furrer, T. Franz, C. Pacher, R. F. Werner, R. Schnabel. Implementation of continuous-variable quantum key distribution with composable and one-sided-device-independent security against coherent attacks. Nat. Commun., 6, 8795(2015).
[36] E. Diamanti, H.-K. Lo, B. Qi, Z. Yuan. Practical challenges in quantum key distribution. npj Quantum Inf., 2, 16025(2016).
[37] A. Furusawa, J. L. Sørensen, S. L. Braunstein, C. A. Fuchs, H. J. Kimble, E. S. Polzik. Unconditional quantum teleportation. Science, 282, 706-709(1998).
[38] M. Huo, J. Qin, J. Cheng, Z. Yan, Z. Qin, X. Su, X. Jia, C. Xie, K. Peng. Deterministic quantum teleportation through fiber channels. Sci. Adv., 4, eaas9401(2018).
[39] N. Takei, H. Yonezawa, T. Aoki, A. Furusawa. High-fidelity teleportation beyond the no-cloning limit and entanglement swapping for continuous variables. Phys. Rev. Lett., 94, 220502(2005).
[40] X. Jia, X. Su, Q. Pan, J. Gao, C. Xie, K. Peng. Experimental demonstration of unconditional entanglement swapping for continuous variables. Phys. Rev. Lett., 93, 250503(2004).
[41] X. Su, C. Tian, X. Deng, Q. Li, C. Xie, K. Peng. Quantum entanglement swapping between two multipartite entangled states. Phys. Rev. Lett., 117, 240503(2016).
[42] X. Li, Q. Pan, J. Jing, J. Zhang, C. Xie, K. Peng. Quantum dense coding exploiting a bright Einstein-Podolsky-Rosen beam. Phys. Rev. Lett., 88, 047904(2002).
[43] J. Mizuno, K. Wakui, A. Fususawa, M. Sasaki. Experimental demonstration of entanglement-assisted coding using a two-mode squeezed vacuum state. Phys. Rev. A, 71, 012304(2005).
[44] Y. Liu, Z. Ma, H. Kang, D. Han, M. Wang, Z. Qin, X. Su, K. Peng. Experimental test of error-tradeoff uncertainty relation using a continuous-variable entangled state. npj Quantum Inf., 5, 68(2019).
[45] Y. Liu, H. Kang, D. Han, X. Su, K. Peng. Experimental test of error-disturbance uncertainty relation with continuous variables. Photon. Res., 7, A56-A60(2019).
[46] Y.-R. Zhang, L.-H. Shao, Y. Li, H. Fan. Quantifying coherence in infinite-dimensional systems. Phys. Rev. A, 93, 012334(2016).
[47] J. Xu. Quantifying coherence of Gaussian states. Phys. Rev. A, 93, 032111(2016).
[48] D. Buono, G. Nocerino, G. Petrillo, G. Torre, G. Zonzo, F. Illuminati. Quantum coherence of Gaussian states(2016).
[49] F. Albarelli, M. G. Genoni, M. G. A. Paris. Generation of coherence via Gaussian measurements. Phys. Rev. A, 96, 012337(2017).
[50] A. Serafini, M. G. A. Paris, F. Illuminati, S. De Siena. Quantifying decoherence in continuous variable systems. J. Opt. B, 7, R19-R36(2005).
[51] F. A. S. Barbosa, A. S. Coelho, A. J. de Faria, K. N. Cassemiro, A. S. Villar, P. Nussenzveig, M. Martinelli. Robustness of bipartite Gaussian entangled beams propagating in lossy channels. Nat. Photonics, 4, 858-861(2010).
[52] X. Deng, S. Hao, C. Tian, X. Su, C. Xie, K. Peng. Disappearance and revival of squeezing in quantum communication with squeezed state over a noisy channel. Appl. Phys. Lett., 108, 081105(2016).
[53] X. Deng, C. Tian, X. Su, C. Xie. Avoiding disentanglement of multipartite entangled optical beams with a correlated noisy channel. Sci. Rep., 7, 44475(2017).
[54] Y. Liu, K. Zheng, H. Kang, D. Han, M. Wang, L. Zhang, X. Su, K. Peng. Distillation of Gaussian Einstein-Podolsky-Rosen steering with noiseless linear amplification(2020).
[55] X. Deng, Y. Liu, M. Wang, X. Su, K. Peng. Sudden death and revival of Gaussian Einstein–Podolsky–Rosen steering in noisy channels. npj Quantum Inf., 7, 65(2021).
[56] S. Suciu, A. Isar. Quantum coherence of two-mode systems in a thermal environment. Rom. J. Phys., 61, 1474-1482(2016).
[57] A. Croitoru, I. Ghiu, A. Isar. Dynamics of quantum coherence in Gaussian open systems. Rom. Rep. Phys., 72, 102(2020).
[58] D. N. S.-S. de Buruaga, C. Sabn. Quantum coherence in the dynamical Casimir effect. Phys. Rev. A, 95, 022307(2017).
[59] M. Zhang, H. Kang, M. Wang, F. Xu, X. Su, K. Peng. Quantifying quantum coherence of optical cat states. Photon. Res., 9, 887-892(2021).
[60] R. Simon. Peres-Horodecki separability criterion for continuous variable systems. Phys. Rev. Lett., 84, 2726-2729(2000).
[61] A. S. Holevo, M. Sohma, O. Hirota. Capacity of quantum Gaussian channels. Phys. Rev. A, 59, 1820-1828(1999).
[62] J. Eisert, N. J. Cerf, M. M. Wolf, G. Leuchs, E. S. Polzik. Gaussian quantum channels. Quantum Information with Continuous Variables of Atoms and Light, 23-42(2007).
[63] S. Bougouffa, Z. Ficek. Delayed transfer of entanglement to initially populated qubits. Phys. Rev. A, 102, 043720(2020).
[64] S. Steinlechner, J. Bauchrowitz, T. Eberle, R. Schnabel. Strong Einstein-Podolsky-Rosen steering with unconditional entangled states. Phys. Rev. A, 87, 022104(2013).

Set citation alerts for the article
Please enter your email address



