- Photonics Research
- Vol. 11, Issue 3, 442 (2023)
Abstract
1. INTRODUCTION
Phase contrast imaging is an essential label-free imaging technique because it enables the visualization of biological processes at multiple scales and resolutions in a non-invasive manner, providing a unique tool for cell division [1], intracellular dynamics [2], phenotypic screening [3], etc. It manipulates scattered radiation through optical field modulations to convert the phase information of non-self-luminous and non-absorbing samples into intensity signals. One of the most classical phase contrast imaging methods is based on interferometric imaging [usually quantitative, also known as quantitative phase imaging (QPI)] [4–7], whose highest spatial frequency, however, is confined to coherent diffraction limit
Partially coherent illumination endows phase contrast imaging with the superiority of high robustness and significantly extended lateral resolution, prompting its applications in biological imaging. The pioneering techniques in this field, such as Zernike phase contrast and differential interference contrast (DIC), have become standard solutions for cellular and subcellular observation [8–12]. Recent advances in partially coherent imaging have further boosted to the development of a series of QPI techniques, such as transport-of-intensity equation (TIE) [13–15], differential phase contrast (DPC) [16–18], and Fourier ptychographic microscopy (FPM) [19–24]. These techniques quantify the optical path length fluctuations across transparent samples and acquire three-dimensional (3D) quantitative phase, enabling phase contrast imaging to move from “qualitative” to “quantitative” [15,25–28]. Because of their superior imaging performance and flexible experimental configuration, QPI techniques have demonstrated their great potential in diverse biological applications [29–32].
QPI by DPC with partially coherent imaging is realized through asymmetric illumination modulation and deconvolution reconstruction, providing speckle-free imaging and twice the lateral resolution of the coherent diffraction limit [33,34]. It estimates the quantitative phase distribution of the sample from the measured intensities, which is considered to solve an inverse problem [35,36]. A strict and correct “intensity-phase” model is required to achieve accurate phase retrieval. However, mutual incoherence of the illumination points results in the nonlinear (or, more precisely, bilinear) dependence of the partially coherent field on the sample properties, which makes it a daunting challenge to recover the sample phase through intensity inversion. Thus, the primary task of QPI with partially coherent imaging is to accurately explain the nonlinear (bilinear) image generation model, a fundamental issue of great importance for the development of QPI. A well-established model is based on the transmission cross-coefficient (TCC) model, which establishes a four-dimensional (4D) expression on the pairs of spatial frequencies of the sample in the spatial frequency domain [37,38] so that the contribution of the sample- and system-dependent parts are represented separately. In addition, the phase-space representations, expressed through 4D Winger functions in the joint spatial frequency domain, model its bilinear characteristics with the advantage of separating the imaging system and the sample [39–42]. However, these high-dimensional representations are difficult to obtain precisely, while their massive data and computation costs make it impractical to recover sample information.
The preferred solution to achieve QPI under partially coherent imaging is to simplify the bilinear transmission of image information as linear properties. For this purpose, the sample (or object) approximations, including weak/slowly varying object approximation [17,33], Born/Rytov approximation [43,44], and multi-slice scattering approximation [45], have been proposed, all of which brought new insights into QPI. For example, weak object approximation considers the amplitude of the scattered light is much smaller than that of the unscattered light, linearizing the relationship between recorded intensity and sample transmission [46,47]. Then, a regularization deconvolution solver is proposed to recover the quantitative phase of the sample [17,48]. Slowly varying object approximation establishes a phase-gradient sensitive mechanism, leading to a “lookup table” correspondence between the measured intensity and the sample phase gradient [49,50]. However, the introduction of approximations means that the imaging performance of the algorithms derived from them is limited by how well the real sample matches the approximation model, making accurate phase (thickness) reconstruction of diverse samples from QPI alone difficult. Moreover, the explicit definitions of these approximations in existing work are still poorly understood. These limitations may result in QPI losing its proudest “quantitative” properties and no longer providing credible evidence for subsequent analyses such as cell morphology and cell mass measurement [51,52].
In this paper, we explore the strict definition of weak object approximation and further propose an iterative deconvolution DPC QPI technique that achieves accurate quantitative phase reconstruction without any additional acquisition, allowing QPI to be extended for biology applications of large-phase samples. The strict definition of weak object approximation is explicitly stated: the one-step deconvolution method could obtain accurate quantitative phase results only when the sample phase is not greater than 0.5 rad. Furthermore, to overcome the difficulty of applying DPC to large-phase samples, we introduce a pseudo-weak object approximation to model the complex transmittance function of the sample and propose an iterative deconvolution algorithm to achieve accurate QPI without additional data acquisition. The iterative process is performed with a deconvolution solver to refine the phase; thus, the phase components can be fully decoupled from the acquisition intensity. We conduct an experiment using a standard microlens array with a large phase of 37 rad (23 μm) and verify that the proposed method yields a quantitative phase consistent with the nominal value. Furthermore, the experiment results on MCF-7 cells accurately present the 3D morphological distribution of the cells, which demonstrates great potential for cell morphology and cell mass measurements.
2. STRICT WEAK OBJECT APPROXIMATION CONDITION
A. Quantitative Phase Imaging by DPC Based on Weak Object Approximation
QPI based on partially coherent imaging provides better lateral resolution and immunity to the system’s imperfections by simultaneously illuminating the sample from multiple angles in a mutually incoherent manner. The light intensity follows Abbe diffraction theory [53], i.e., mutual incoherence of the illumination points leads to the incoherent superposition of the intensity caused by each point. The cross propagation and superposition of each point often result in the nonlinear (or, more precisely, bilinear) dependence of the partially coherent field on the sample properties [37,38,54]:
This equation illustrates that TCC is determined by the illumination function
Object approximation is the most common method for simplifying the partially coherent imaging model to a mathematically analytic form [34]. Weak object approximation achieves the linearization of the intensity expression, establishing an effective phase inversion mechanism (the forward model of partially coherent imaging and QPI algorithm are given in Appendices A and B). It requires the phase terms of the sample to be very weak (usually much less than 1 rad), and then the complex transmittance function of the sample
This expression ignores a series of higher-order terms in phase and retains only its primary term, successfully separating the DC (background) and phase terms into the real and imaginary parts of the complex distribution. Then, a linear expression of mutual intensity is substituted into Eq. (1) to obtain the intensity distribution under the weak phase approximation [55],
DPC adopts asymmetric illumination, a flexible and convenient implementation without mechanical manipulation, to achieve an oddly symmetric WPTF and evenly symmetric absorption transfer function [16,17]. Consequently, a simple differential calculation can be implemented to eliminate the background item from Eq. (4), and only linear phase items are left in
This leads to a linear relationship between the phase of the sample and the acquired intensity, and the quantitative phase information can then be reconstructed by Fourier space deconvolution with the WPTF [16–18,56]. Tikhonov regularization is commonly used to solve the ill-posed problem to obtain a stable approximate solution,
B. Illumination and Nonlinear Error of Weak Object Approximation
Weak object approximation simplifies partially coherent imaging; however, it also limits the applicability of the phase inversion algorithm. Specifically, only if the weak object condition is met can the quantitative phase distribution of the sample be recovered accurately without distortions and artifacts. Otherwise, DPC will suffer from severe nonlinear errors and lose its nature of “quantitative.” The analysis of the theoretical model of the deconvolution solution reveals that two approximations are involved in its derivation. On the one hand, weak object approximation linearizes the complex transmittance function of the sample by omitting the higher-order terms in its Taylor expanded form, as shown in Eq. (3). On the other hand, the higher-order scattering terms are ignored to derive the analytical expression of the WPTF, as shown in Eq. (4). Although the two approximations jointly contribute to the deconvolution reconstruction algorithm, the intensity difference of Eq. (5) eliminates the nonlinear error caused by the latter approximation. Thus, the reconstruction error in the DPC deconvolution mainly arises from the mismatch between the ideal sample function
Figure 1 explains the information mismatch between the actual and linear intensity model under weak object approximation with different illumination by numerical simulation. The complex transmittance functions of
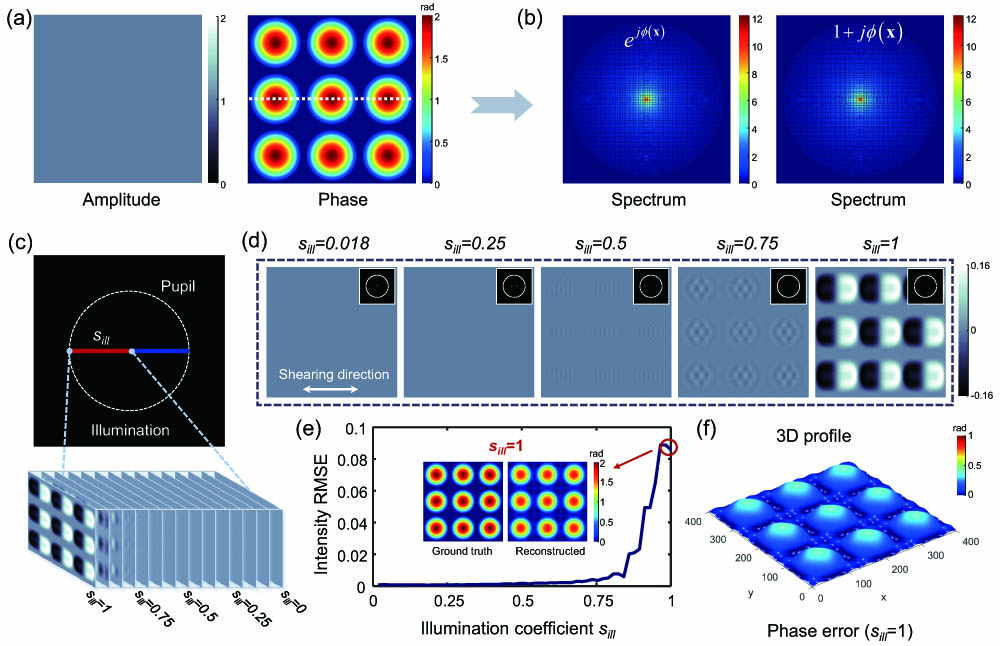
Figure 1.Simulation and comparison of ideal intensity model and weak object approximation intensity model under different illumination coefficients. (a) Ground-truth amplitude and phase images of the complex transmittance function used to simulate the sample. (b) Spectrum distribution of the theoretical sample distribution
C. Strict Weak Object Approximation Condition
The well-defined weak object approximation is the basis for guaranteeing the accuracy of quantitative phase reconstruction, while it also allows the imaging performance of QPI to be measured and analyzed in an informed manner. However, due to the complex theoretical derivation of the deconvolution solver, it is challenging to determine the strict definition of weak object approximation from the mathematical expression. To address this problem, we analyzed the imaging performance of DPC QPI at maximum nonlinear error to explore the strict weak object approximation definition applicable to all samples and illumination apertures. Two representative samples of a slowly varying microlens array and three sharply varying steps were selected as target samples, and their phase amplitudes can be adjusted arbitrarily. Meanwhile, the illumination aperture can be set from half-circle to half-annulus to simulate different illuminations. The largest nonlinear error will arise when the sample of three sharply varying steps is illuminated by a half-annular aperture with the maximum illumination coefficient. In this case, an accurate reconstruction of the sample phase using the one-step deconvolution will serve as the basis for the strict definition of weak object approximation.
Figure 2 shows the numerical simulation results for two representative samples with varying phases from 0.2 rad to 2 rad under different illumination apertures. As shown in Fig. 2(a), three types of illumination apertures were set, including a half-circular aperture, a half-annular aperture of 0.5 width, and a half-annular illumination of 0.01 width with the maximum illumination coefficient. The half-circular aperture and the half-annular aperture of 0.01 width correspond to two extremes of the nonlinear error. Specifically, the intensity superposition under a half-circular illumination weakens the nonlinear error; however, this error will exist in the intensity with the maximum weight under the half-annular illumination of 0.01 width. To quantitatively measure the reconstruction errors, the RMSE values between these reconstructed phases and the ground-truth phases are calculated to plot the numerical curves. As shown in Figs. 2(b) and 2(c), the reconstruction error increases monotonically with increasing phase amplitude. This indicates that the difference between the acquired intensity and the linear intensity desired by the one-step deconvolution increases when imaging samples with larger phases. The reconstructed phase of the sharply varying step sample under the half-annular illumination of 0.01 width results in a more serious reconstruction error, which is consistent with our inference. To measure phase reconstruction performance, an RMSE value of less than 1% was used to determine the accurate reconstructed phase since the reconstruction error can be almost neglected in this case. From Figs. 2(b) and 2(c), when the phase is less than or equal to 0.5 rad, the reconstruction RMSE at any sample and illumination aperture is less than 1%. Therefore, the strict weak object approximation is suggested to be defined as not greater than 0.5 rad [
![]()
Figure 2.Numerical simulation results with variable phase to determine the definition of the strict weak object approximation. (a) Illumination apertures and their corresponding WPTFs. (b), (c) RMSE curves for the reconstructed phase of a microlens array and a sharply varying step with increasing phase values under different illumination apertures. (d), (e) Reconstructed phase and its profile for different phase values of a microlens array and a sharply varying step under half-annular illumination of 0.01 width.
3. ITERATIVE DECONVOLUTION BASED ON PSEUDO-WEAK OBJECT APPROXIMATION
To achieve accurate QPI of large-phase objects, we introduce pseudo-weak object approximation in electron microscopy into DPC and develop a more precise object approximation model [57,58]. Considering a sample distribution
Considering the intensity distribution under the DPC difference model, the real part of the intensity spectrum distribution derived from the convolution of the complex transmittance function will be eliminated under asymmetric illumination, leaving only its imaginary part terms. When the sample phase satisfies the strict weak object approximation (
The primary motivation of the iterative reconstruction algorithm is to eliminate the nonlinear components and extract the intensity components that are linearly related to the phase of the large-phase object. Based on pseudo-weak object approximation, the nonlinear intensity error can be obtained by calculating the intensity residual between the forward-generated intensity of partially coherent imaging and the phase-linear correlated intensity. Consequently, the iterative algorithm requires no additional acquisition data (usually four images) and refines the reconstructed phase by a continuous deconvolution solver. In this process, the input intensity used for the deconvolution process is denoted as
The generated intensity images under the same asymmetric axis are used to calculate the phase gradient image
Then, the nonlinear error caused by the mismatch between these two models can be estimated as
During the iterative process,
Then, the phase of the sample is iteratively updated based on the following equation:
The algorithm flow chart of the iterative deconvolution is displayed in Fig. 3. The algorithm begins with the one-step deconvolution reconstruction, where the solved phase is used as the initial phase. In the iterative process, the solved phase and a uniform amplitude construct a complex transmittance function to generate DPC images under asymmetric illuminations based on Abbe’s method. Specifically, the acquired image under partially coherent imaging is represented as a linear superposition of the intensities obtained by multiple point sources independently illuminating objects with the complex distribution of
![]()
Figure 3.Algorithm flow chart of the iterative deconvolution reconstruction.
We demonstrated the imaging performance of iterative deconvolution through numerical simulations. The same microlens distribution similar to the previous simulation is used to generate the DPC images. In order to explore the phase imaging performance of the iterative deconvolution for large-phase objects, we constructed a sample with a phase distribution of
![]()
Figure 4.Simulation results of one-step deconvolution and iterative deconvolution for large-phase samples with different illumination apertures. (a), (b) Comparison of phase results for reconstruction by two methods under half-circular illumination aperture and annular illumination aperture.
4. EXPERIMENTAL VALIDATION
To verify the phase reconstruction accuracy of iterative deconvolution, several experiments were conducted on different samples. The experimental system was built on a commercial inverted microscope platform (Olympus, IX73), and its illumination source was replaced by a programmable LED array with a spacing of 2 μm to flexibly implement asymmetric illumination at a wavelength of 504 nm. In image acquisition process, four illumination patterns (left, right, up, and down) were switched, and the transmitted light field information of the sample was collected by an objective lens with
A. Quantitative Morphological Characterization of Microlens Arrays
To quantitatively demonstrate the accuracy of the iterative deconvolution method for reconstructing the phase, a standard microlens array sample [SUSS, Microoptics, refractive index (RI) of 1.46] with a curvature radius of 350 μm and a pitch of 250 μm was used as the target. It was placed in water with a dielectric RI of 1.33, so its theoretical height of 23 μm corresponds to a phase amplitude of 37 rad. Figures 5(a1), 5(a2) and 5(b1), 5(b2) display the asymmetric illumination patterns and the phase gradient images in two directions along the corresponding shearing directions. These captured images were used to perform the one-step deconvolution reconstruction directly, and the reconstructed phase is shown in Fig. 5(d1). A significantly weaker phase contrast can be found, indicating that the reconstructed phase in the traditional one-step deconvolution method is smaller than the theoretical phase value of the microlens array. The acquired images were then used to implement the proposed iterative deconvolution method (which takes several minutes). Figure 5(c) shows the variation curve of the intensity differences in iterations [Eq. (13)], which gradually converges to a stable small value as the iteration number increases. Once there is a constant minimum error between the estimated and acquired intensities, the iteration will be terminated, and the final iteration result will be output, as shown in Fig. 5(d2). We further selected one microlens unit as the region of interest (ROI) for the quantitative characterization of its 3D morphology, and the results are shown in Figs. 5(e1), 5(e2) and 5(f1), 5(f2), respectively. From the 3D pseudo-color morphological distribution in Figs. 5(f1) and 5(f2), the iterative deconvolution correctly characterizes the true 3D morphology of the microlens, which is difficult to achieve by one-step deconvolution. Finally, in order to quantitatively compare the numerical accuracy of the reconstructed phases under these two algorithms, we extracted the quantitative phase values along the white dashed and plotted the curve in Figs. 5(g1) and 5(g2). It verifies that the iterative deconvolution algorithm provides reliable quantitative phase data for subsequent research and analysis.
![]()
Figure 5.Experiment results on a standard microlens array sample (SUSS, Microoptics, RI of 1.46) with a curvature radius of 350 μm and a pitch of 250 μm. (a1), (a2) Asymmetrical illumination patterns. (b1), (b2) Differential intensity images along different shearing directions. (c) Variation curve of the intensity error. (d1) and (d2), (e1) and (e2) Reconstructed phases and their ROI under one-step deconvolution and iterative deconvolution. (f1) and (f2) 3D pseudo-color morphological distribution. (g1) and (g2) Quantitative phase values along the white dashed.
B. Morphological Detection of Biological Cells
Morphological detection of biological cells is critical for the early confirmation of cancer treatment, where the cell changes during malignant transformation can be quantified by studying morphology, membrane dynamics, and cell refraction indices. DPC QPI provides a reliable pathology testing means for cancer tissues and cells. We conducted an experiment on MCF-7 human breast cancer cells to compare the cell morphology testing performance of one-step deconvolution and iterative deconvolution algorithms. During sample preparation, the MCF-7 cells were placed in 4% paraformaldehyde solution without any staining and labeling treatment. Figure 6 displays the reconstructed results under one-step deconvolution and iterative deconvolution. We adopted the Tikhonov regularization and introduced a suitable regularization parameter for both deconvolution processes. In Fig. 6(a), we show the field-of-view (FOV) reconstructed phase under iterative deconvolution. Then, the phase values along the white dashed line were extracted to plot the quantitative curves, yielding the results in Figs. 6(b) and 6(c), respectively. It can be clearly observed that for mitotic cells with large phase values, one-step deconvolution (blue curve) provides a degraded cell morphology feature, while the iterative deconvolution (red curve) accurately recovers both low-frequency and high-frequency quantitative features of the sample, demonstrating accurate 3D morphological data. Figures 6(d1)–6(g1) and 6(d2)–6(g2) present the enlarged phase of four ROIs under one-step deconvolution and iterative deconvolution. Compared to the one-step deconvolution algorithm, the iterative deconvolution algorithm recovers the cellular contours and the internal subcellular structures with highly accurate quantitative phase distribution. A 3D pseudo-color rendering image and a quantitative profile are then plotted to characterize the 3D morphological distribution of MCF-7 cells, as shown in Fig. 6(h). It can be found that the iterative deconvolution demonstrates a more significant cell thickness, which provides more accurate morphological detection data for cell analysis.
![]()
Figure 6.Experiment results on MCF-7 human breast cancer cells. (a) FOV reconstructed phase under the iterative deconvolution. (b), (c) Phase values along the white dashed line. (d1)–(g1), (d2)–(g2) Enlarged images of the four ROIs under one-step deconvolution and iterative deconvolution. (h) 3D display of reconstruction results and the quantitative phase profiles.
5. CONCLUSION
In this paper, we have explored the strict definition of weak object approximation under partially coherent imaging and proposed an iterative deconvolution algorithm to achieve accurate QPI for large-phase objects. By exploring the imaging performance of QPI under weak object approximation with different illumination coherence and sample distribution, the strict weak object approximation is defined as a sample with a phase no greater than 0.5 rad. Thus, QPI by DPC enables accurate quantitative phase reconstruction for arbitrarily samples and illumination apertures. Furthermore, an iterative deconvolution QPI algorithm based on pseudo-weak object approximation was proposed to go beyond weak object approximation, achieving accurate QPI for large-phase objects without any additional acquisition. As a result, QPI by DPC is no longer limited by the premise of weak object approximation and can be applied to the high-precision phase characterization and measurement of large-phase samples. We demonstrated the accuracy of the proposed method using a standard microlens array sample with a large phase. Compared with the conventional one-step deconvolution, the proposed method more accurately recovers a phase consistent with the nominal value. The experiment on MCF-7 cells demonstrated that our method accurately reflects the 3D morphological data of the cells, which will provide strong support for subsequent cell morphology and cell mass analysis. Our method will enable the quantitative nature of DPC QPI and provide a powerful tool for the quantitative characterization and measurement of biological applications with large-phase objects.
In QPI techniques based on partially coherent imaging, weak object approximation and slowly varying object approximation are the two most general approximation models. Unlike weak object approximation, which requires the absolute phase of the object to be very small, slowly varying object approximation requires that the difference between the sample phase and its neighborhood is much less than 1 rad. Although these two approximations are defined from different perspectives, they can be equivalent when some other approximations are introduced [15]. For example, the quantitative phase of a sample with a slowly varying phase and weak absorption can be solved by the weak phase deconvolution algorithm, which means that the deconvolution solver based on weak object approximation can be relaxed to a slowly varying object. It is also important to mention that, to simplify the model, we analyzed the DPC QPI of a pure phase object, whose nonlinear errors originate only from the higher order terms of the phase. As for samples with both absorption and phase [
Acknowledgment
Acknowledgment. We thank Ran Ye from Nanjing Normal University for discussing the writing of the manuscript.
APPENDIX A: FORWARD MODEL OF PARTIALLY COHERENT IMAGING
Partially coherent imaging provides better lateral resolution and immunity to the system’s imperfections by simultaneously illuminating the sample from multiple angles in a mutually incoherent manner. The light intensity follows Abbe diffraction theory [
Equation (
For non-self-luminous and non-absorbing samples, QPI is an inverse problem of estimating the sample phase from measured intensities. The appropriate optical modulations (manipulation of the scattered radiation) are required to generate an effective (non-zero) TCC response. Thus, the phase information of the sample can be transferred into the acquired intensity signals. Oblique illumination and defocusing CTF are two widely developed means of phase modulation, and the developed QPI technologies are called TIE (defocusing-based) [
APPENDIX B: DECONVOLUTION QUANTITATIVE PHASE SOLVER UNDER WEAK OBJECT APPROXIMATION
In order to efficiently extract the phase components from the intensity measurement, weak or slowly varying object approximations are introduced in QPI to simplify the complex transmittance function of the sample [
This expression ignores a series of higher-order terms in phase and retains only its primary term, successfully separating the DC and phase terms into the real and imaginary parts of the linearized complex distribution. To reanalyze the forward model of Eq. (
Notice that the second approximation is considered by omitting the interference terms between the scattered light, which just corresponds to the first-order Born approximation commonly used in diffraction tomography. Such a linear expression of mutual intensity is then substituted into Eq. (
Since the sample phase distribution
DPC adopts asymmetric illumination, a flexible and convenient implementation without mechanical manipulation, to achieve an oddly symmetric WPTF and an evenly symmetric absorption transfer function [
Solving for the phase distribution of the sample from the acquired intensity is an ill-posed problem, which can obtain a stable approximate solution by the regularization method. In DPC, Tikhonov regularization is a common solver for such an inverse algorithm,
APPENDIX C: ILLUMINATION COHERENCE AND ITERATIVE DECONVOLUTION ALGORITHM
To explore the effect of weak object approximation on DPC, we analyzed the deconvolution reconstruction error under different illumination apertures through numerical simulations. The complex transmittance functions of the samples were set to
Next, the illumination aperture was set as an annular illumination aperture with a width of 0.01, which corresponds to the acquisition intensity with the worst nonlinear characteristics. We used the same parameter configuration as the circular illumination to explore the reconstruction errors of weak object approximation under annular illumination, and the simulation results are shown in Fig.
![]()
Figure 7.Simulation of one-step deconvolution reconstruction under half-circular illumination. (a), (b) Ground-truth amplitude and phase images of the complex transmittance function used to simulate the sample. (c), (d) WPTF and synthetic WPTF. (e1), (f1) Spectrum of the theoretical sample distribution
![]()
Figure 8.Simulation of one-step deconvolution reconstruction under half-annular illumination. (a), (b) Ground-truth amplitude and phase images of the complex transmittance function used to simulate the sample. (c), (d) WPTF and synthetic WPTF. (e1), (f1) Spectrum of the theoretical sample distribution
References
[8] F. Zernike. Phase contrast. Z Tech Physik, 16, 454(1935).
[10] W. Lang. Nomarski Differential Interference-Contrast Microscopy(1982).
[11] G. Nomarski. Nouveau dispositif pour lobservation en contraste de phase differentiel. J. Phys. Radium, 16, S88(1955).
[26] G. Popescu. Quantitative phase imaging of nanoscale cell structure and dynamics. Methods Cell Biol., 90, 87-115(2008).
[32] G. Popescu. Quantitative Phase Imaging of Cells and Tissues(2011).
[35] M. Bertero. Introduction to Inverse Problems in Imaging(2020).
[36] R. W. Gerchberg. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik, 35, 237-246(1972).
[37] H. H. Hopkins. On the diffraction theory of optical images. Proc. R. Soc. London Ser. A. Math. Phys. Sci., 217, 408-432(1953).
[41] J. Ojeda-Castañeda, E. Sicre. Bilinear optical systems. Opt. Acta, 31, 255-260(1984).
[46] J. M. Cowley. Diffraction Physics(1995).
[47] E. J. Kirkland. Advanced Computing in Electron Microscopy, 12(1998).
[54] T. Wilson, C. Sheppard. Theory and Practice of Scanning Optical Microscopy, 180(1984).
[59] W. Singer, M. Totzeck, H. Gross. Handbook of Optical Systems, 2(2005).

Set citation alerts for the article
Please enter your email address



