We propose a modified supervised learning algorithm for optical spiking neural networks, which introduces synaptic time-delay plasticity on the basis of traditional weight training. Delay learning is combined with the remote supervised method that is incorporated with photonic spike-timing-dependent plasticity. A spike sequence learning task implemented via the proposed algorithm is found to have better performance than via the traditional weight-based method. Moreover, the proposed algorithm is also applied to two benchmark data sets for classification. In a simple network structure with only a few optical neurons, the classification accuracy based on the delay-weight learning algorithm is significantly improved compared with weight-based learning. The introduction of delay adjusting improves the learning efficiency and performance of the algorithm, which is helpful for photonic neuromorphic computing and is also important specifically for understanding information processing in the biological brain.
- Photonics Research
- Vol. 9, Issue 4, B119 (2021)
Abstract
1. INTRODUCTION
As the improvement of traditional neural networks has gradually approached an upper limit, research focuses on neural networks with more biological reality. The spiking neural networks (SNNs), normally known as the third generation of artificial neural networks (ANNs), are more biologically plausible than previous ANNs [1] and have attracted more and more attention in recent decades [2–6]. Spikes transmitted in the biological neural networks enable the network to capture the rich dynamics of neurons and to integrate different information dimensions [3]. However, the information representation and processing manner has become a controversial issue and remains very challenging.
Rate coding is widely used in traditional SNNs; however, there is biological evidence that the precise timing of spikes also conveys information in nervous systems [7–9]. The precise timing of spikes enables higher information encoding capacity and lower power consumption [10–12], which are extremely important in information processing of the human brain. However, the exact learning mechanism still remains an open problem [13]. It has been shown that in the cerebellum and the cerebellar cortex, there exist signals that act like an instructor that helps the processing of information [14,15]. Several supervised learning algorithms have been proposed upon which specific problems that are tightly related to neural processing such as spike sequence learning and pattern recognition have been solved successfully [16–20]. Remote supervised method (ReSuMe) is one of the supervised learning algorithms originally derived from the well-known Widrow-Hoff rule [17]. Based on photonic spike-timing-dependent plasticity (STDP) and anti-STDP rules, the synaptic weights can be adjusted to train the output neuron to fire spikes at the desired time.
Time-delayed transmission is an intrinsic feature in neural networks. Biological evidence shows that the transmission velocities in the nervous system can be modulated [21,22], for example, by changing the length and thickness of dendrites and axons [23]. The adjustability of both delay and weight of a synapse is referred to as synaptic plasticity. Delay plasticity has also been found to be helpful for the neuron in changing its firing behavior and synchronization, and it helps to understand the process of learning [24,25]. Delay selection and delay shift are two basic approaches incorporated in delay learning works [26,27]. To be specific, delay selection is to strengthen the weight of an optimal synapse among multiple subconnections, and delay shift is a more biologically plausible method training neurons to fire with coincident input spikes and with constant weight. Recently, researchers found that combined adjustment of delay and weight enhances the performance of an SNN [28–32]. In 2015, a delay learning remote supervised method (DL-ReSuMe) for spiking neurons was proposed to merge the delay shift approach and weight adjustment based on ReSuMe, by which the learning accuracy and learning speed are enhanced [30]. In 2018, Taherkhani
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
For the sake of emulating realistic biological behaviors, SNN hardware realizations are designed to seek ultralow power consumption [5]. Devices for the implementation of basic elements of SNN, namely, artificial spiking neurons and synapses, have been achieved via complementary metal-oxide-semiconductors (CMOS), transistors, and the emerging nonvolatile memory technologies [33–38], etc. Photonic neuromorphic systems have attracted attention for being a potential candidate in applications of ultrafast processing. Despite its similarity with biological neurons [39], the semiconductor laser also exceeds its electronic counterpart in its ultrafast response and low power consumption. Numerous studies on photonic synapses and photonic neurons [40–53] have laid a solid foundation for significant progress in photonic neuromorphic computing based on both software and hardware implementations [54–59]. In 2019, an all-optical SNN with self-learning capacity was physically implemented on a nanophotonic chip, which is capable of supervised and unsupervised learning [55]. In 2020, we proposed to solve XOR in an all-optical neuromorphic system with inhibitory dynamics of a single photonic spiking neuron based on vertical-cavity surface-emitting lasers (VCSELs) with an embedding saturable absorber (VCSEL-SA) [58], and an all-optical spiking neural network based on VCSELs was also proposed for supervised learning and pattern classification [59]. However, as far as we know, delay learning has not yet been applied in photonic SNNs.
In this work, we propose to incorporate delay learning with the traditional algorithm based on an optical SNN. First, we propose a modified algorithm that combines delay learning with ReSuMe in a photonic SNN, which adjusts synaptic weight and delay simultaneously. By implementing a spike sequence learning task, better performance and learning efficiency of the proposed algorithm than that of its weight-based counterpart are verified. Then, the proposed algorithm is also implemented for classification, where two benchmarks, the Iris data set and the breast cancer data set, are adopted. By applying the delay-weight (DW)-based algorithm, the testing accuracy for both benchmarks is significantly improved (reaching 92%).
2. SYSTEM MODEL
A. Photonic Neurons and Synapses Based on VCSEL-SA and VCSOA
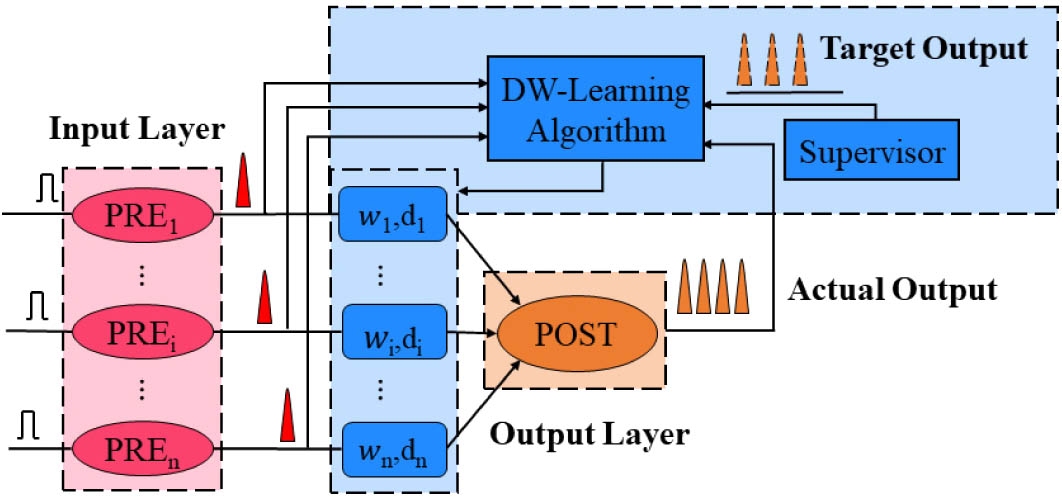
Figure 1.Schematic diagram of DW-based learning in a single-layer photonic SNN.
The photonic neurons and synapses are the basic elements in a photonic SNN. VCSEL-SA can mimic spiking dynamics of a biological neuron [51] and VCSEL that works below threshold value can serve as a vertical-cavity semiconductor optical amplifier (VCSOA) that is able to perform the STDP function [47], which provides possibilities of large-scale integration and low power consumption in a photonic SNN. In this work, the spiking dynamics are implemented via the excitable VCSEL-SA neurons. The rate equations of a VCSEL-SA are written as follows [57]:
The term
B. DW-Based Learning Algorithm
![]()
Figure 2.Schematic illustration of the ReSuMe incorporated with optical STDP rule.
The term
![]()
Figure 3.(a1) and (b1) Input pattern and output pattern before delay adjustment. (a2) and (b2) After 7 training epochs.
3. RESULTS AND DISCUSSION
![]()
Figure 4.Comparison of the learning capability of a single neuron based on (a) weight-based ReSuMe and (b) DW-ReSuMe. The value of SSD after the 50th, 100th, and 300th training epoch is presented for different
However, note that if the desired output contains more than one spike, the delay learning window
A. Spike Sequence Learning
![]()
Figure 5.(a1) Carrier density of the POST after training and (b1) the evolution of output spikes based on the DW-ReSuMe; (a2) and (b2) those based on ReSuMe. The black solid line is
![]()
Figure 6.Evolution of (a1) synaptic weights
![]()
Figure 7.Learning spike sequences with ununiformed ISI. (a1) and (b1) The evolution of output spikes for spike sequence [10 ns, 12 ns, 14 ns, 18 ns, 20 ns, 22 ns, 24 ns, 26 ns, 29 ns] and [10 ns, 11 ns, 13 ns, 14.5 ns, 17 ns, 21 ns, 23 ns, 25.5 ns, 27 ns], respectively. (a2) and (b2) The evolution for the corresponding distance.
B. Fisher’s Iris Data Set
The Fisher’s Iris flower data set (Fisher, 1936) is a classic benchmark of pattern recognition that contains three classes of Iris flowers with a total of 150 case entries [31]. One of the classes is linearly separable from the other two, while the other two classes are linearly inseparable. Four measurements are used to describe and differentiate the three classes, and each measurement is directly encoded into single spike firing at different times and is linearly rescaled into the interval of [5 ns, 10 ns]. The network comprises 4 PREs and a single POST. The encoding spikes are fed into the 4 PREs of the SNN via synapses with adjustable delay and weight. The initial delays are 2 ns for all of the four input neurons, and the initial weight
![]()
Figure 8.(a) Training accuracy and (b) testing accuracy varying with training epochs for weight-based ReSuMe (blue solid line) and DW-ReSuMe (red solid line).
![]()
Figure 9.Illustration of classification results for (a) training data set and (b) testing data set. The orange cycles denote target spiking time, the blue squares represent the actual spiking time, and misclassified samples are highlighted in bright blue.
![]()
Figure 10.Testing accuracy as a function of (a) weight learning window
C. Breast Cancer Data Set
![]()
Figure 11.(a) Training accuracy and (b) testing accuracy varying with training epochs based on DW-ReSuMe (red solid line) and ReSuMe (blue solid line), respectively.
![]()
Figure 12.(a1) Training accuracy and (a2) testing accuracy for the Iris data set after 60 training epochs with different initial delay
![]()
Figure 13.Learning accuracy of the breast cancer data set based on DW-ReSuMe with different cases of
DW-based learning has shown excellent performance in single-layer networks. However, the real neural networks are usually hierarchical, and synaptic weights and delays can be modulated based on different biological mechanisms, which form the foundations of complex brain functions. It is quite interesting and challenging to consider how to effectively introduce delay adjustment into deep learning networks.
4. CONCLUSION
This paper proposed a supervised DW learning method in an optical SNN. Based on precise timing of spikes, delay learning trains coherent inputs in the input layer of an SNN via shifting the synaptic delays according to the desired and actual output timing. The proposed DW-ReSuMe is applied to spike sequence learning and two classification benchmarks, the Iris data set and breast cancer data set, successfully. The performance of the SNN is significantly improved compared with its weight-based counterpart. By introducing time-delay learning in a photonic SNN, fewer optical neurons are required to solve different tasks, which is significant to photonic neuromorphic computing. The results also suggest that synaptic delay and weight may be a combined learning mechanism in real biological neural networks, which deserves deeper investigation.
References
[1] S. Ghosh-Dastidar, H. Adeli. Spiking neural networks. Int. J. Neural Syst., 19, 295-308(2009).
[2] R. Brette, M. Rudolph, T. Carnevale, M. Hines, D. Beeman, J. M. Bower, M. Diesmann, A. Morrison, P. H. Goodman, F. C. Harris, M. Zirpe, T. Natschläger, D. Pecevski, B. Ermentrout, M. Djurfeldt, A. Lansner, O. Rochel, T. Vieville, E. Muller, A. P. Davison, S. El Boustani, A. Destexhe. Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci., 23, 349-398(2007).
[3] N. Kasabov, K. Dhoble, N. Nuntalid, G. Indiveri. Dynamic evolving spiking neural networks for on-line spatio- and spectro-temporal pattern recognition. Neural Netw., 41, 188-201(2013).
[4] K. Roy, J. Akhilesh, P. Priyadarshini. Towards spike-based machine intelligence with neuromorphic computing. Nature, 575, 607-617(2019).
[5] W. Q. Zhang, B. Gao, J. S. Tang, P. Yao, H. Q. Wu. Neuro-inspired computing chips. Nat. Electron., 3, 371-382(2020).
[6] T. Clarence, M. Arlija, N. Kasabov. Spiking neural networks: background, recent development and the NeuCube architecture. Neural Process. Lett., 3, 1675-1701(2020).
[7] A. Cariani. Temporal codes and computations for sensory representation and scene analysis. IEEE Trans. Neural Netw., 15, 1100-1111(2004).
[8] S. M. Bohte. The evidence for neural information processing with precise spike-times: a survey. Natural Comput., 3, 195-206(2004).
[9] A. Mohemmed, S. Schliebs. Training spiking neural networks to associate spatio-temporal input-output spike patterns. Neurocomputing, 107, 3-10(2013).
[10] S. B. Laughlin, R. R. de Ruyter van Steveninck, J. C. Anderson. The metabolic cost of neural information. Nat. Neurosci., 1, 36-41(1998).
[11] S. B. Laughlin. Energy as a constraint on the coding and processing of sensory information. Curr. Opinion Neurobiol., 11, 475-480(2001).
[12] H. Paugam-Moisy, S. Bohte. Computing with spiking neuron networks. Handbook of Natural Computing, 335-376(2012).
[13] J. Hu, H. Tang, K. C. Tan, H. Li, L. Shi. A spike-timing-based integrated model for pattern recognition. Neural Comput., 25, 450-472(2013).
[14] F. Ponulak, A. Kasinski. Introduction to spiking neural networks: information processing, learning and applications. Acta Neurobiol. Experim., 71, 409-433(2011).
[15] H. Jörntell, C. Hansel. Synaptic memories upside down: bidirectional plasticity at cerebellar parallel fiber-Purkinje cell synapses. Neuron, 52, 227-238(2006).
[16] R. Gütig, H. Sompolinsky. The tempotron: a neuron that learns spike timing-based decisions. Nat. Neurosci., 9, 420-428(2006).
[17] F. Ponulak, A. Kasinski. Supervised learning in spiking neural networks with ReSuMe: sequence learning, classification, and spike shifting. Neural Comput., 22, 467-510(2010).
[18] I. Sporea, A. Grüning. Supervised learning in multilayer spiking neural networks. Neural Comput., 25, 473-509(2013).
[19] S. R. Kulkarni, B. Rajendran. Spiking neural networks for handwritten digit recognition—supervised learning and network optimization. Neural Netw., 103, 118-127(2018).
[20] C. Hong, X. Wei, J. Wang, B. Deng, H. Yu, Y. Che. Training spiking neural networks for cognitive tasks: a versatile framework compatible with various temporal codes. IEEE Trans. Neural Netw. Learn. Syst., 31, 1285-1296(2020).
[21] S. Boudkkazi, L. Fronzaroli-Molinieres, D. Debanne. Presynaptic action potential waveform determines cortical synaptic latency. J. Physiol., 589, 1117-1131(2011).
[22] J. W. Lin, D. S. Faber. Modulation of synaptic delay during synaptic plasticity. Trends Neurosci., 25, 449-455(2002).
[23] C. W. Eurich, K. Pawelzik, U. Ernst, J. D. Cowan, J. G. Milton. Dynamics of self-organized delay adaptation. Phys. Rev. Lett., 82, 1594-1597(1999).
[24] X. B. Gong, Y. B. Wang, B. Ying. Delay-induced firing behavior and transitions in adaptive neuronal networks with two types of synapses. Sci. China Chem., 56, 222-229(2012).
[25] M. Dhamala, V. K. Jirsa, M. Ding. Enhancement of neural synchrony by time delay. Phys. Rev. Lett., 92, 074104(2004).
[26] S. Ghosh-Dastidar, H. Adeli. Improved spiking neural networks for EEG classification and epilepsy and seizure detection. Integr. Comput.-Aided Eng., 14, 187-212(2007).
[27] P. Adibi, M. R. Meybodi, R. Safabakhsh. Unsupervised learning of synaptic delays based on learning automata in an RBF-like network of spiking neurons for data clustering. Neurocomputing, 64, 335-357(2005).
[28] S. Ghosh-Dastidar, H. Adeli. A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection. Neural Netw., 22, 1419-1431(2009).
[29] A. Taherkhani, A. Belatreche, Y. Li, L. P. Maguire. EDL: an extended delay learning based remote supervised method for spiking neurons. Neural Information Processing, 190-197(2015).
[30] A. Taherkhani, A. Belatreche, Y. Li, L. P. Maguire. DL-ReSuMe: a delay learning-based remote supervised method for spiking neurons. IEEE Trans. Neur. Netw. Learn. Syst., 26, 3137-3149(2015).
[31] A. Taherkhani, A. Belatreche, Y. Li, L. P. Maguire. A supervised learning algorithm for learning precise timing of multiple spikes in multilayer spiking neural networks. IEEE Trans. Neur. Netw. Learn. Syst., 29, 5394-5407(2018).
[32] M. L. Zhang, J. B. Wu, A. Belatreche, Z. H. Pan, X. R. Xie, Y. S. Chua. Supervised learning in spiking neural networks with synaptic delay-weight plasticity. Neurocomputing, 409, 103-118(2020).
[33] W. Xu, S. Y. Min, H. Hwang, T. W. Lee. Organic core-sheath nanowire artificial synapses with femtojoule energy consumption. Sci. Adv., 2, e1501326(2016).
[34] I. Sourikopoulos, S. Hedayat, C. Loyez, F. Danneville, V. Hoel, E. Mercier, A. Cappy. A 4-fJ/spike artificial neuron in 65 nm CMOS technology. Front. Neurosci., 11, 123(2017).
[35] J. D. Zhu, Y. C. Yang, R. D. Jia, Z. X. Liang, W. Zhu, Z. A. Rehman, L. Bao, X. X. Zhang, Y. M. Cai, L. Song, R. Huang. Ion gated synaptic transistors based on 2D van der Waals crystals with tunable diffusive dynamics. Adv. Mater., 30, 1800195(2018).
[36] B. Irem, L. G. Manuel, S. R. Nandakumar, M. Timoleon, P. Thomas, R. Bipin, L. Yusuf, S. Abu, E. Evangelos. Neuromorphic computing with multi-memristive synapses. Nat. Commun., 9, 2514(2018).
[37] Y. Zhou, N. Xu, B. Gao, Y. Y. Chen, B. Y. Dong, Y. Li, Y. H. He, X. S. Miao. Complementary graphene-ferroelectric transistors (C-GFTs) as synapses with modulatable plasticity for supervised learning. IEEE International Electron Devices Meeting (IEDM), 1-4(2019).
[38] S. G. Hu, G. C. Qiao, Y. A. Liu, L. M. Rong, Q. Yu, Y. Liu. An improved memristor model connecting plastic synapse synapses and nonlinear spiking neuron. J. Phys. D, 52, 275402(2019).
[39] J. Ohtsubo, R. Ozawa, M. Nanbu. Synchrony of small nonlinear networks in chaotic semiconductor lasers. Jpn. J. Appl. Phys., 54, 072702(2015).
[40] A. Hurtado, I. D. Henning, M. J. Adams. Optical neuron using polarization switching in a 1550 nm-VCSEL. Opt. Express, 18, 25170-25176(2010).
[41] A. Hurtado, K. Schires, I. Henning, M. Adams. Investigation of vertical cavity surface emitting laser dynamics for neuromorphic photonic systems. Appl. Phys. Lett., 100, 103703(2012).
[42] M. P. Fok, Y. Tian, D. Rosenbluth, P. R. Prucnal. Pulse lead/lag timing detection for adaptive feedback and control based on optical spike-timing-dependent plasticity. Opt. Lett., 38, 419-421(2013).
[43] Q. Li, Z. Wang, Y. Le, C. Sun, X. Song, C. Wu. Optical implementation of neural learning algorithms based on cross-gain modulation in a semiconductor optical amplifier. Proc. SPIE, 10019, 100190E(2016).
[44] S. Y. Xiang, Y. H. Zhang, X. X. Guo, J. F. Li, A. J. Wen, W. Pan, Y. Hao. Cascadable neuron-like spiking dynamics in coupled VCSELs subject to orthogonally polarized optical pulse injection. IEEE J. Sel. Top. Quantum Electron., 23, 1700207(2017).
[45] T. Deng, J. Robertson, A. Hurtado. Controlled propagation of spiking dynamics in vertical-cavity surface-emitting lasers: towards neuromorphic photonic networks. IEEE J. Sel. Top. Quantum Electron., 23, 1800408(2017).
[46] Z. G. Chen, R. Carlos, W. H. P. Pernice, C. D. Wrigh, H. Bhaskara. On-chip photonic synapse. Sci. Adv., 3, e1700160(2017).
[47] S. Y. Xiang, J. K. Gong, Y. H. Zhang, X. X. Guo, A. Wen, Y. Hao. Numerical implementation of wavelength-dependent photonic spike timing dependent plasticity based on VCSOA. IEEE J. Quantum Electron., 54, 8100107(2018).
[48] Y. H. Zhang, S. Y. Xiang, J. K. Gong, X. X. Guo, A. J. Wen, Y. Hao. Spike encoding and storage properties in mutually coupled vertical-cavity surface-emitting lasers subject to optical pulse injection. Appl. Opt., 57, 1731-1737(2018).
[49] I. Chakraborty, G. Saha, A. Sengupta, K. Roy. Toward fast neural computing using all-photonic phase change spiking neurons. Sci. Rep., 8, 12980(2018).
[50] I. Chakraborty, G. Saha, K. Roy. Photonic in-memory computing primitive for spiking neural networks using phase-change materials. Phys. Rev. Appl., 11, 014063(2019).
[51] Y. H. Zhang, S. Y. Xiang, X. Guo, A. Wen, Y. Hao. All-optical inhibitory dynamics in photonic neuron based on polarization mode competition in a VCSEL with an embedded saturable absorber. Opt. Lett., 44, 1548-1551(2019).
[52] J. Robertson, E. Wade, Y. Kopp, J. Bueno, A. Hurtado. Toward neuromorphic photonic networks of ultrafast spiking laser neurons. IEEE J. Sel. Top. Quantum Electron., 26, 7700715(2020).
[53] B. W. Ma, W. W. Zou. Demonstration of a distributed feedback laser diode working as a graded-potential-signaling photonic neuron and its application to neuromorphic information processing. Sci. China Inf. Sci., 63, 160408(2020).
[54] S. Y. Xiang, Y. H. Zhang, J. K. Gong, X. X. Guo, L. Lin, Y. Hao. STDP-based unsupervised spike pattern learning in a photonic spiking neural network with VCSELs and VCSOAs. IEEE J. Sel. Top. Quantum Electron., 25, 1700109(2019).
[55] J. Feldmann, N. Youngblood, C. D. Wright, H. Bhaskaran, W. H. P. Pernice. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature, 569, 208-215(2019).
[56] C. Ríos, N. Youngblood, Z. Cheng, M. L. Gallo, W. H. P. Pernice, C. D. Wright, A. Sebastian, H. Bhaskaran. In-memory computing on a photonic platform. Sci. Adv., 5, eaau5759(2019).
[57] Z. W. Song, S. Y. Xiang, Z. X. Ren, G. Q. Han, Y. Hao. Spike sequence learning in a photonic spiking neural network consisting of VCSELs-SA with supervised training. IEEE J. Sel. Top. Quantum Electron., 26, 1700209(2020).
[58] S. Y. Xiang, Z. X. Ren, Y. H. Zhang, Z. W. Song, Y. Hao. All-optical neuromorphic XOR operation with inhibitory dynamics of a single photonic spiking neuron based on VCSEL-SA. Opt. Lett., 45, 1104-1107(2020).
[59] S. Y. Xiang, Z. X. Ren, Z. W. Song, Y. H. Zhang, X. X. Guo, G. Q. Han, Y. Hao. Computing primitive of fully-VCSELs-based all-optical spiking neural network for supervised learning and pattern classification. IEEE Trans. Neural Netw.(2020).
[60] S. Moallemi, R. Welker, J. Kitchen. Wide band programmable true time delay block for phased array antenna applications. IEEE Dallas Circuits and Systems Conference (DCAS), 1-4(2016).
[61] G. Wetzstein, A. Ozcan, S. Gigan, S. Fan, D. Englund, M. Soljačić, C. Denz, D. A. B. Miller, D. Psaltis. Inference in artificial intelligence with deep optics and photonics. Nature, 588, 39-47(2020).
[62] A. Roy, S. Govil, R. Miranda. An algorithm to generate radial basis function (RBF)-like nets for classification problems. Neural Netw., 8, 179-201(1995).

Set citation alerts for the article
Please enter your email address



