Abstract
In this paper, we examine the tiny polarization rotation effect in total internal reflection due to the spin–orbit interaction of light. We find that the tiny polarization rotation rate will induce a geometric phase gradient, which can be regarded as the physical origin of photonic spin Hall effect. We demonstrate that the spin-dependent splitting in position space is related to the polarization rotation in momentum space, while the spin-dependent splitting in momentum space is attributed to the polarization rotation in position space. Furthermore, we introduce a quantum weak measurement to determine the tiny polarization rotation rate. The rotation rate in momentum space is obtained with 118 nm, which manifests itself as a spatial shift, and the rotation rate in position space is achieved with , which manifests itself as an angular shift. The investigation of the polarization rotation characteristics will provide insights into the photonic spin Hall effect and will enable us to better understand the spin–orbit interaction of light.1. INTRODUCTION
The origin of spin–orbit interaction of light in reflection is attributed to the transverse nature of the photonic polarization: The polarizations of angular spectrum components experience different rotations in order to satisfy the transversality. The photonic spin Hall effect (SHE), manifesting itself as spin-dependent splitting of light in both position and momentum spaces, is considered as a result of the spin–orbit interaction of light [1–3]. In partial reflection, the polarization rotation only appears in momentum space, and the geometric phase gradient induces a spin-dependent splitting in position space [4–9]. The spin-dependent splitting in photonic SHE is generally on subwavelength scales, which can be observed by the signal enhancement technique known as quantum weak measurements [10,11].
However, there has been relatively little attention paid to the tiny polarization rotation effect in position space. In this paper, we examine the position-space polarization rotation in total internal reflection. Unlike in partial reflection, we find that the polarization rotation appears in both momentum and position spaces. We demonstrate that the spin-dependent splitting in position space is related to the polarization rotation in momentum space, while the spin-dependent splitting in momentum space is attributed to the polarization rotation in position space. To distinguish and detect the two kinds of spin-dependent splitting, a modified experimental scheme of weak measurements is proposed. The polarization characteristics of each wave-vector component can be determined by the spin-dependent splitting, and tiny polarization rotation rates are achieved.
2. POLARIZATION ROTATION IN POSITION AND MOMENTUM SPACES
We consider a light beam reflection at a prism–air interface. The plane of the laboratory Cartesian frame is parallel to the prism–air interface. We use the coordinate frames and to denote incident and reflect beams, respectively. The axis attaches to the direction of the central wave vector. We assume that the wavepacket with or polarization reflects at the prism–air interface. The corresponding individual wave-vector components of and are expressed by and [3]: Here, and are the incident angle and refracted angle, respectively; and are the incident and refracted wave vectors, respectively. After reflection, , , and the polarization states evolve as where and . Equations (3) and (4) show that a tiny rotation arises after reflection at the prism–air interference.
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
In partial reflection, the Fresnel coefficients are real numbers. Thus, both and are also real numbers. In the total internal reflection, however, the Fresnel coefficients are complex, and Here, and are the absolute values of the complex reflected Fresnel coefficients; and denote their arguments. Therefore, the complex shifts arise. From Eqs. (5) and (6), we obtain Here, and for partial reflection. However, , , and generally for total internal reflection. Note that the phase difference between the two popularization states can be applied to determine the beam shifts [12].
In the spin basis set, the polarization of or can be decomposed into two orthogonal polarization components and , where and represent the left- and right-circular polarization components, respectively. The wavefunction in momentum space can be specified by the following expression: where is the width of the wavefunction.
For input polarization, the reflected wavefunction in the momentum space can be obtained as Here, denotes the spin–orbit coupling, and since the spin–orbit interaction is weak at the interface reflection [13].
Note that the complex shift can be written as . They should have different contributions to the transverse shift in the far field. We first consider the real part of the complex shift, and the polarization state after reflection can be written as The photonic SHE can be described as a consequence of geometric phase which arises from the spin–orbit interaction. The spin-dependent phase in position space can be written as where . The spin-dependent splitting in position space is induced by the phase gradient in momentum space, which can be written as
We next consider the imaginary part of the complex shift. The polarization state in position space can be obtained by Fourier transformation: Here, represents the Rayleigh length. The spin-dependent phase in position space can be written as The corresponding spin-dependent splitting in momentum space can be obtained as In fact, the spin-dependent splitting in momentum space manifests itself as an angular shift , which ultimately induces a spatial shift in position space. It should be mentioned that this shift increases linearly during propagation: .
The spin-dependent splitting in photonic SHE can be regarded as the combined contribution of real and imaginary parts of the complex shift. For input polarization, the spin-dependent splitting can be written as Similarly, spin-dependent splitting for the input polarization can be given by Here, the real part of the complex shift is related to the spin-dependent splitting in position space while the imaginary part is associated with spin-dependent splitting in momentum space.
We now examine the polarization rotation in the photonic SHE. From Eqs. (13) and (16), the polarization states can be expressed in term of the Jones matrix: where and ; and are the polarization rotation rate in position and momentum spaces, respectively. Therefore, the polarization rotation rate will induce a geometric phase gradient which can be regarded as the physical origin of photonic SHE.
We plot the polarization distributions in total internal and partial reflection as shown in Fig. 1. In total internal reflection at the prism–air interface, the polarization rotation present in position and momentum space [Figs. 1(a) and 1(c)]. Therefore, the geometric phase gradient and spin-dependent splitting should also occur in momentum space and position space. In partial reflection at the air–prism interface, the polarization rotation is only present in the momentum space [Figs. 1(b) and 1(d)]. Correspondingly, the geometric phase gradient only appears in momentum space, which ultimately induces the spin-dependent splitting in position space as shown in Eq. (15). Therefore, the spin-dependent splitting in position space is attributable to the polarization rotation in momentum space, while the splitting in momentum space is attributed to the polarization rotation in position space.
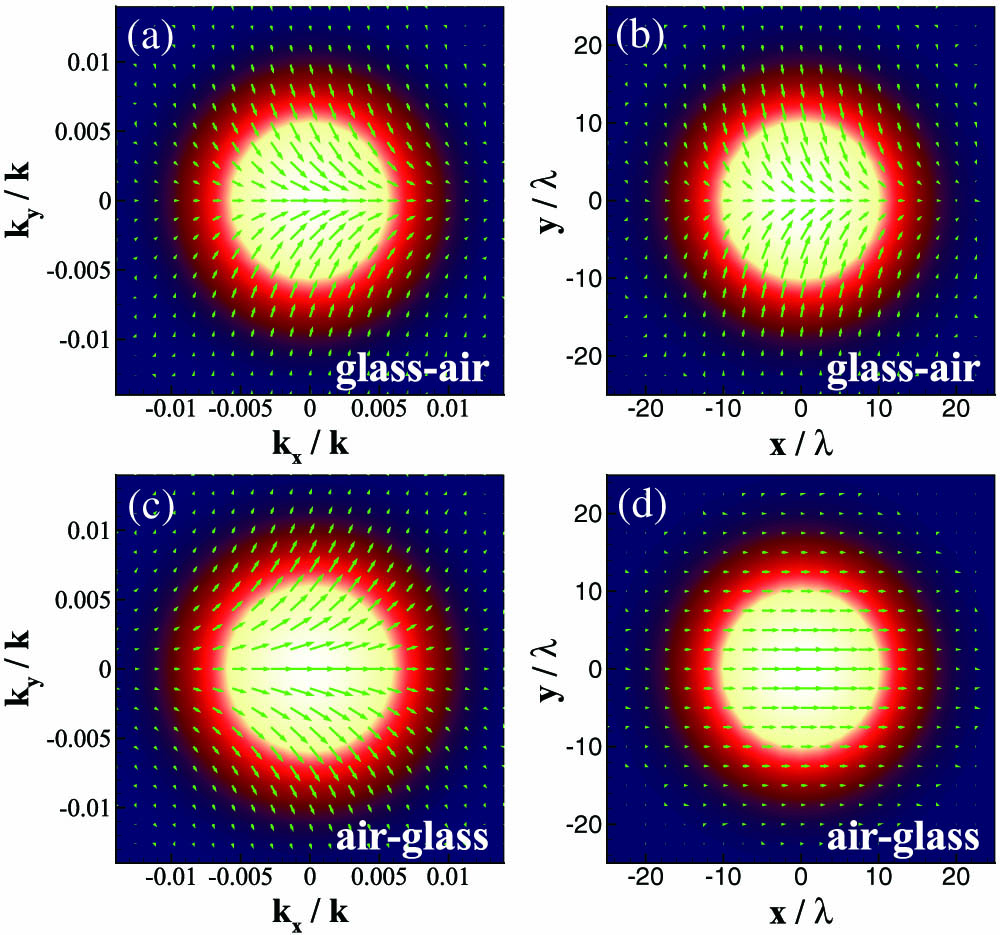
Figure 1.Polarization rotation of light beam in total internal reflection at glass–air interface and in partial reflection at air–glass interface. (a) and (c) Polarization rotation in momentum space. (b) and (d) Polarization rotation in position space. The incident angle is chosen as . To make the polarization rotation characteristics more noticeable, we amplify the rotation angles by 100 times.
3. POLARIZATION ROTATION AND WEAK MEASUREMENTS
The tiny polarization rotation rate can be determined by the measurements of the spin-dependent splitting. Here, a modified experimental setup of weak measurements is proposed (see Fig. 2). A linear Gaussian with the wavelength is generated by the He–Ne laser. The lenses of L1 and L2 have corresponding 50 and 250 mm focal lengths; they are used for focusing and collimating the light beam. Glan laser polarizer (GLP1), together with quarter-wave plate (QWP) and GLP2, provides the preselected and postselected states, respectively. After the preselection of state, weak interaction, and the postselection of state, the wave function evolves to the final state: Here, is the so-called weak value and is given by where is the Pauli operator, and and are the polarization states of the preselection and postselection in the Poincaré sphere, respectively.
![Experimental setup for observation of the spin-dependent splitting in photonic SHE with complex weak values. The He–Ne laser inputs a linearly polarized Gaussian beam; prisms have refractive index n=1.515 (BK7 at 632.8 nm); the half-wave plate (HWP) for adjusting the intensity of light beam; the lenses L1 and L2 have 50 and 280 mm focal lengths, respectively; the GLP1 and GLP2 and the QWP together provide the preselected and postselected states; and the CCD will be used for capturing the intensity profiles. The inset represent the preselected and postselected angles on a Poincaré sphere. Note that the experiment setup is slightly different from those in Refs. [5,6]; in the present case the QWP has been introduced to modulate the preselected state.](/Images/icon/loading.gif)
Figure 2.Experimental setup for observation of the spin-dependent splitting in photonic SHE with complex weak values. The He–Ne laser inputs a linearly polarized Gaussian beam; prisms have refractive index (BK7 at 632.8 nm); the half-wave plate (HWP) for adjusting the intensity of light beam; the lenses L1 and L2 have 50 and 280 mm focal lengths, respectively; the GLP1 and GLP2 and the QWP together provide the preselected and postselected states; and the CCD will be used for capturing the intensity profiles. The inset represent the preselected and postselected angles on a Poincaré sphere. Note that the experiment setup is slightly different from those in Refs. [5,6]; in the present case the QWP has been introduced to modulate the preselected state.
In our case, both and are complex. However, only the imaginary part of can be amplified and is given by Here, the imaginary and real parts of complex shifts are determined by the real and imaginary parts of the weak values, respectively. Note that the complex weak value has been interpreted as spatial and angular shifts in the Goos–Hänchen and Imbert–Fedorov effects [14,15].
The preselected and postselected states can be on a Poincaré sphere: where and represent quantum state on the Poincaré sphere [16], and are preselected angle and postselected angle, respectively. For input polarization and , while for input polarization and . Substituting Eqs. (25) and (26) into Eq. (23), we obtain the complex weak value as Here, the real and imaginary parts of the complex weak value can be switched by preselection and postselection of states, respectively.
We now consider the amplified spatial shift in the far field. After a free evolution, the wavepacket moves to its final position, When the initial shift is complex, it is difficult to distinguish and detect the real and imaginary parts, since they have combined contribution to the transverse shift in the far field. Therefore, a single measurement with a purely real weak value has difficulty distinguishing them.
To detect the complex shifts, two different schemes should be involved: First a purely imaginary weak value and second a purely real weak value. We first consider the case where the weak value is purely imaginary. The preselected angle is chosen as in Eq. (27); and are obtained. The imaginary weak value will only amplify the spin-dependent shifts in position space. From Eq. (28), the amplified shift in the far-field region can be written as The large beam shifts will be obtained in the far-field region for . The amplified spatial displacement varies with as shown in Figs. 3(a) and 3(c). For input polarization, the initial shift in position space is 118.2 nm, while for input polarization, the initial shift is 117.8 nm [Figs. 3(b) and 3(d)]. We find that the initial shifts remain unchanged with the postselected angle . The tiny shift in position space can be regarded as the result of the geometric phase gradient in momentum space as shown in Eq. (15). Therefore, the tiny polarization rotation rate in momentum space with is achieved. Note that the modified model of weak measurements should be introduced when the preselected and postselected states are nearly orthogonal [17].

Figure 3.Transverse spatial displacement of initial and final displacement when the polarization states of the incident light beam are and , namely and . (a) and (c) show the amplified shift of and , respectively. (b) and (d) are the corresponding initial spin-dependent splitting in position space. Insets in (a) and (c) represent the preselected and postselected angles on Poincaré spheres, respectively.
We next consider that the weak value is purely real. We thus choose the postselection angle as in Eq. (27), and then get and . The amplified shifts for and polarization are given by Here, the weak value will only amplify the spin-dependent shifts in momentum space. The amplified spatial displacement varies with as shown in Figs. 4(a) and 4(c). The angular shifts with are obtained for both and input polarization [Figs. 4(b) and 4(d)]. The initial spin-dependent splitting in momentum space of the two spin components are the same in size while opposite in direction, which is independent of the postselection angle. The tiny polarization rotation rate in position space with is achieved.

Figure 4.Transverse angular displacement of initial and final displacement as a function of preselection angle. (a) and (c) show the amplified shift of and , respectively. (b) and (d) are the corresponding initial spin-dependent splitting in momentum space. Insets in (a) and (c) represent the preselected and postselected angles on the Poincaré spheres.
4. CONCLUSION
In conclusion, we have revealed the tiny polarization rotation effect in total internal reflection due to the spin–orbit interaction of light. We have found that the spin-dependent splitting in position space is related to the polarization rotation in momentum space, while the spin-dependent splitting in momentum space is attributed to the polarization rotation in position space. The quantum weak measurement with complex weak values has been applied to detect the tiny polarization rotation effect. The tiny effect of polarization rotation in both position and momentum spaces should occur when the Fresnel coefficients are complex. Therefore, these results are not restricted to the total internal reflection and could be extended to other optical systems, such as metallic reflection [18,19], layered nanostructures [20], and two-dimensional atomic crystals [21]. In addition, the spin–momentum locking and unidirectional propagation of evanescent wave in total internal reflection has attracted much attention [22–24]. Analogous with the behavior of electrons in the quantum SHE, this phenomenon can be called the quantum SHE of light. The investigations of polarization rotation in the SHE may provide insights into the fundamental properties of spin–orbit interaction of light.
References
[1] M. Onoda, S. Murakami, N. Nagaosa. Hall effect of light. Phys. Rev. Lett., 93, 083901(2004).
[2] K. Y. Bliokh, Y. P. Bliokh. Conservation of angular momentum, transverse shift, and spin Hall effect in reflection and refraction of an electromagnetic wave packet. Phys. Rev. Lett., 96, 073903(2006).
[3] O. Hosten, P. Kwiat. Observation of the spin Hall effect of light via weak measurements. Science, 319, 787-790(2008).
[4] A. Aiello, J. P. Woerdman. Role of beam propagation in Goos–Hänchen and Imbert–Fedorov shifts. Opt. Lett., 33, 1437-1439(2008).
[5] Y. Qin, Y. Li, H. He, Q. Gong. Measurement of spin Hall effect of reflected light. Opt. Lett., 34, 2551-2553(2009).
[6] H. Luo, X. Zhou, W. Shu, S. Wen, D. Fan. Enhanced and switchable spin Hall effect of light near the Brewster angle on reflection. Phys. Rev. A, 84, 043806(2011).
[7] L. Kong, X. Wang, S. Li, Y. Li, J. Chen, B. Gu, H. Wang. Spin Hall effect of reflected light from an air–glass interface around the Brewster angle. Appl. Phys. Lett., 100, 071109(2012).
[8] Y. Lv, Z. Wang, Y. Jin, M. Cao, L. Han, P. Zhang, H. Li, H. Gao, F. Li. Spin polarization separation of light reflected at Brewster angle. Opt. Lett., 37, 984-986(2012).
[9] X. Qiu, Z. Zhang, L. Xie, J. Qiu, F. Gao, J. Du. Incident-polarization-sensitive and large in-plane-photonic spin-splitting at the Brewster angle. Opt. Lett., 40, 1018-1021(2015).
[10] Y. Aharonov, D. Z. Albert, L. Vaidman. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett., 60, 1351-1354(1988).
[11] J. Dressel, M. Malik, F. M. Miatto, A. N. Jordan, R. W. Boyd. Colloquium: understanding quantum weak values: basics and applications. Rev. Mod. Phys., 86, 307-316(2014).
[12] C. Prajapati, S. Pidishety, N. K. Viswanathan. Polarimetric measurement method to calculate optical beam shifts. Opt. Lett., 39, 4388-4391(2014).
[13] K. Y. Bliokh, F. J. Rodríguez-Fortuño, F. Nori, A. V. Zayats. Spin–orbit interactions of light. Nat. Photonics, 9, 796-808(2015).
[14] M. R. Dennis, J. B. Götte. The analogy between optical beam shifts and quantum weak measurements. New J. Phys., 14, 073013(2012).
[15] S. Goswami, M. Pal, A. Nandi, P. K. Panigrahi, N. Ghosh. Simultaneous weak value amplification of angular Goos–Hänchen and Imbert–Fedorov shifts in partial reflection. Opt. Lett., 39, 6229-6232(2014).
[16] A. N. Jordan, J. Martínez-Rincón, J. C. Howell. Technical advantages for weak-value amplification: when less is more. Phys. Rev. X, 4, 011031(2014).
[17] S. Chen, X. Zhou, C. Mi, H. Luo, S. Wen. Modified weak measurements for the detection of the photonic spin Hall effect. Phys. Rev. A, 91, 062105(2015).
[18] N. Hermosa, A. M. Nugrowati, A. Aiello, J. P. Woerdman. Spin Hall effect of light in metallic reflection. Opt. Lett., 36, 3200-3202(2011).
[19] X. Zhou, Z. Xiao, H. Luo, S. Wen. Experimental observation of the spin Hall effect of light on a nanometal film via weak measurements. Phys. Rev. A, 85, 043809(2012).
[20] H. Luo, X. Ling, X. Zhou, W. Shu, S. Wen, D. Fan. Enhancing or suppressing the spin Hall effect of light in layered nanostructures. Phys. Rev. A, 84, 033801(2011).
[21] X. Zhou, X. Li, H. Luo, S. Wen. Identifying graphene layers via spin Hall effect of light. Appl. Phys. Lett., 101, 251602(2012).
[22] K. Y. Bliokh, A. Y. Bekshaev, F. Nori. Extraordinary momentum and spin in evanescent waves. Nat. Commun., 5, 3300(2014).
[23] K. Y. Bliokh, D. Smirnova, F. Nori. Quantum spin Hall effect of light. Science, 348, 1448-1451(2015).
[24] T. Van Mechelen, Z. Jacob. Universal spin-momentum locking of evanescent waves. Optica, 3, 118-126(2016).

![]()
![]()
![]()




