Jia Tan, Shengliang Xu, Xu Han, Yueming Zhou, Min Li, Wei Cao, Qingbin Zhang, Peixiang Lu. Resolving and weighing the quantum orbits in strong-field tunneling ionization[J]. Advanced Photonics, 2021, 3(3): 035001
Search by keywords or author
- Advanced Photonics
- Vol. 3, Issue 3, 035001 (2021)
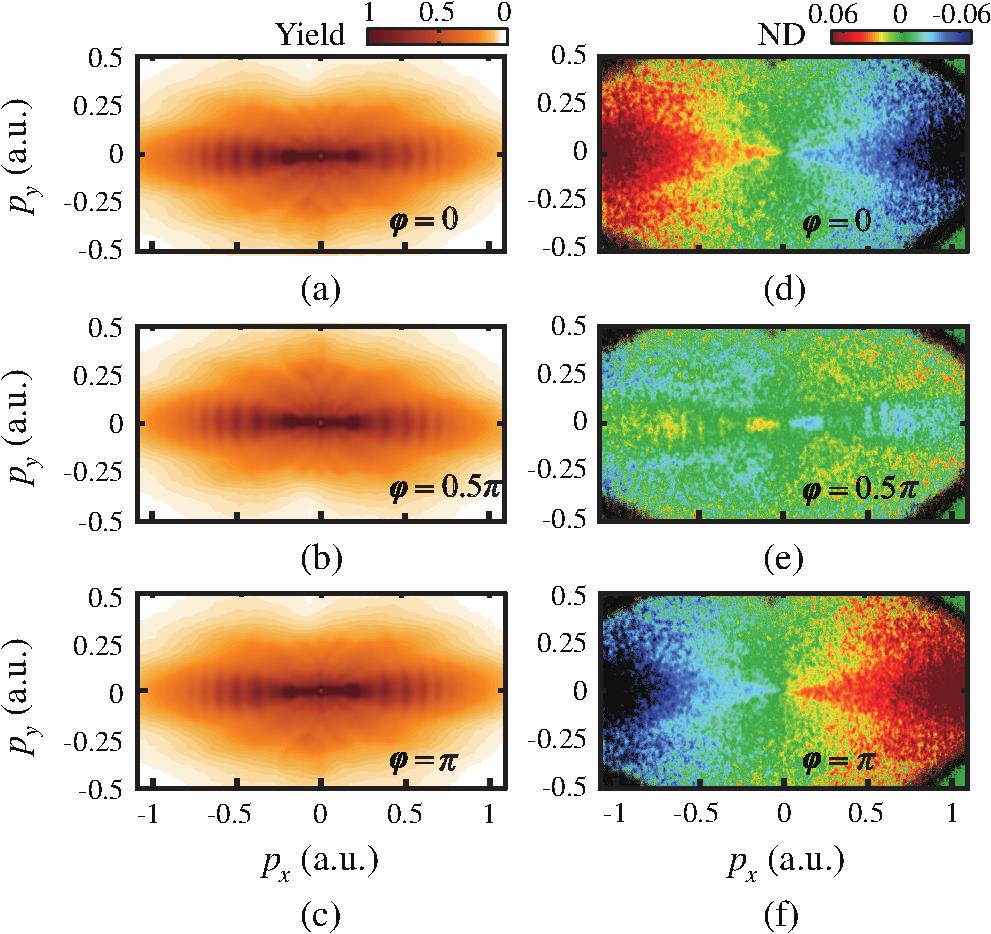
Fig. 1. (a)–(c) The experimentally measured PEMDs for strong-field tunneling ionization of Ar by the parallel two-color (
![(a) The ND as a function of φ for the momentum (px,py)=(−0.6,0.1) a.u. The open circles show the experimental data and the green curve shows the fitted results. (b) The fitted ND by Eq. (2) as a function of φ for the momentum (px,py)=(−0.6,0) (blue curve), (−0.6,0.1) (purple curve), and (−0.6,0.2) a.u. (green curve). The data are normalized such that the maximum of each curve is unity. (c) Same as (b) but for (px,py)=(−0.4,0) (black curve), (−0.5,0) (red curve), and (−0.6,0) a.u. (yellow curve). (d) The optimal phase φm in the region of px∈[−1.1,1.1] a.u. and py∈[−0.5,0.5] a.u. (e) Cuts of φm at px=−0.4 a.u. (red crosses), −0.5 a.u. (green squares), and −0.6 a.u. (blue triangles). The error bars show the 95% confidence interval in fitting.](/richHtml/ap/2021/3/3/035001/img_002.png)
Fig. 2. (a) The ND as a function of
Fig. 3. (a) Illustration of the ionization times of the long and short orbits in strong-field tunneling ionization. The long and short orbits correspond to the ionization events, where the electron is released at the falling and rising edges of electric field, respectively. The blue curve indicates the electric field of the FM field and the red curve shows its vector potential. (b) The
Fig. 4. (a) The ND at

Set citation alerts for the article
Please enter your email address



