- High Power Laser Science and Engineering
- Vol. 10, Issue 2, 02000e15 (2022)
Abstract
Keywords
1 Introduction
In the past decades, many injection schemes for electron beams in the accelerating wakefield excited by laser pulses[1–4] have been proposed and tested. Among them, injection by background density variation[5–12], collinear colliding pulses injection[13–15] and multi-pulse ionization-injection schemes, such as two-color ionization injection[16,17] and resonant multi-pulse ionization injection (ReMPI)[18–20], are very promising in terms of transverse beam quality, being able to generate electron beams with normalized emittances as low as tens of nm, as shown by analytical results and numerical simulations. The usage of circularly polarized laser pulses can be beneficial to lower the threshold for self-injection in the bubble regime[21]. High-quality ionization injection schemes, however, use linearly polarized pulses for the ionizing pulse to minimize the residual transverse momentum, while they may use either linear or circular polarization for the laser pulse (or the pulse train for the ReMPI scheme), which drives the wakefield[16].
Accuracy of numerical simulations of ionization-injection processes can be extremely challenging when schemes providing good-quality beams are investigated, as they are required to accelerate electron bunches suitable to drive an X-ray free-electron laser[22] for the EuPRAXIA project[23] or similar projects based on a high gradient plasma accelerator[24]. This is because the longitudinal grid spacing should be small enough to efficiently resolve the extraction process, occurring in a tiny fraction (usually
In the following, we will suppose that the linearly polarized ionization laser pulse of amplitude
Sign up for High Power Laser Science and Engineering TOC. Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
The theory from Schroeder et al.[31] also shows that, in the optimal conditions of unsaturated ionization, the newborn electrons are extracted in tiny slabs centered at the maxima of the electric field strength
Here,
The possibility of using very accurate predictors of the rms normalized emittance along the polarization axis for either particles extracted in a single cycle or by the whole laser pulse is of paramount importance for high-quality beam production studies. Moreover, as standard requests refer to both high charge and high quality for the beam, working points in a saturated or partially saturated regime are often selected. Motivated by the needs reported above, we recast the theory in Ref. [31] for the local and global bunch parameters, so as to include all the relevant terms of order
2 Setting up the pulse amplitude for tunnel ionization
In the following, the tunnel ionization process occurring in a (single) laser field is considered. The instantaneous ionization rate can be described by the Ammosov–Delone–Krainov (ADK) formula[35–38], expressed in terms of the electric field normalized to the critical ADK field
The choice of the optimal value for the normalized field amplitude
Graphical solutions of Equation (9) for either tens of fs long pulses or near single-cycle pulses can be found in the Appendix.
3 Accurate residual momentum theory for single-cycle lasting ionization
In this section we recast the theory for
3.1 Local properties of the emitted electrons without saturation effects
We start considering the rms values of the extraction phase
It is now straightforward to evaluate the expectation values of
The rms residual momentum
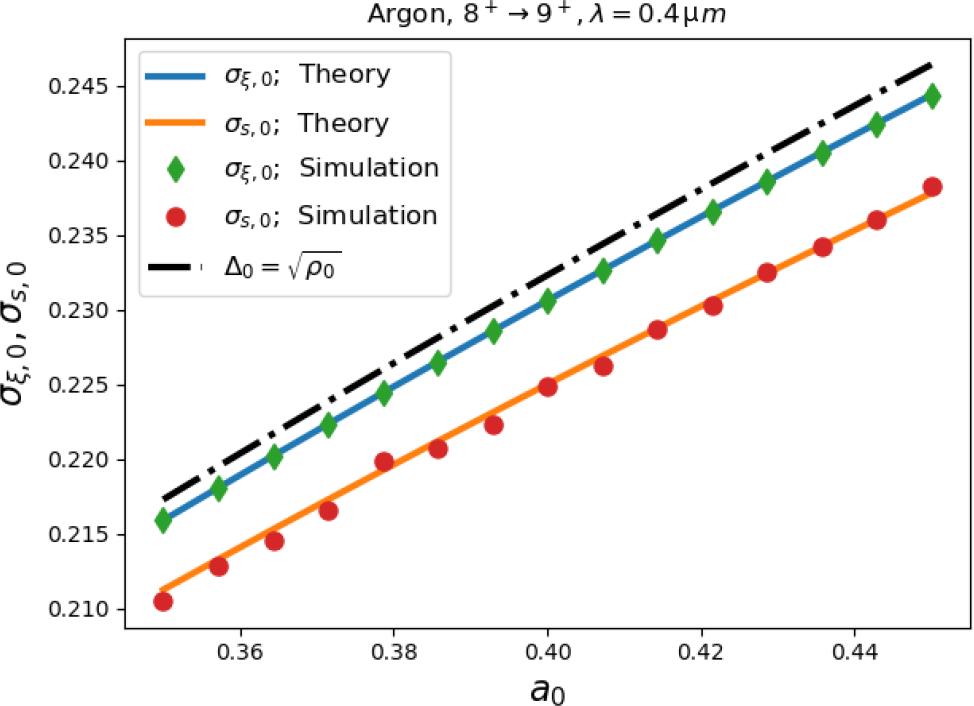
Figure 1.Root mean square values of the local extraction phases  and their sinus as a function of the laser amplitude
and their sinus as a function of the laser amplitude  (
( ) for the process
) for the process  . The blue line shows the analytical results for
. The blue line shows the analytical results for  by Equation (
by Equation ( by Equation (
by Equation ( .
.
3.2 Local, single-channel, ionization process including saturation effects
Local saturation effects may be important when they occur within a single pulse cycle (see Figure 2). In this case, due to the monotonic reduction of the available ions as the pulse proceeds crossing each field peak, an asymmetry of the extraction average phase occurs, thus inducing a deviation of the rms value for
Going more into detail with the rate equation (4), we start expressing the integral
The saturation shape function
is also an accurate predictor, but with expected errors
![]()
Figure 2.Cumulative ionization fraction  (see Equation (
(see Equation ( term (orange full-dashed line). The right-hand axis shows the errors associated either with the theory (black curve) or with the lower order theory without the non-Gaussian
term (orange full-dashed line). The right-hand axis shows the errors associated either with the theory (black curve) or with the lower order theory without the non-Gaussian  correction.
correction.
Once the cumulative ionization function
The statistical local weight of Equation (18) is now employed (instead of
The estimate of the average extraction phase within the peak
The moments
![]()
Figure 3.Statistical moments  for
for  and full saturation correction
and full saturation correction  numerically evaluated as in Equations (
numerically evaluated as in Equations ( for the transition
for the transition  and
and  .
.
Once the extraction phases have been statistically described, the resulting distribution of the residual transverse momenta is finally obtained (once again after neglecting ponderomotive force effects) by evaluating the particle momenta as
It is interesting to note that a slight asymmetry and therefore a visible deviation from the Gaussian distribution occur even at pulse amplitudes corresponding to (or close to) working points used in high-quality beam production simulations (see, e.g., Ref. [19]). This is apparent in Figure 5, where the single peak contributions from the model as well as the full-cycle Monte Carlo and PIC
![]()
Figure 4.Distribution of  for the electrons extracted in a single cycle from argon
for the electrons extracted in a single cycle from argon  ions (
ions ( ,
, 
 corresponding to
corresponding to  ). The blue bars show the distribution obtained by a Monte Carlo simulation. The orange and green bars refer to the distribution obtained in the first and second peak, respectively, inferred by the model of Equation (
). The blue bars show the distribution obtained by a Monte Carlo simulation. The orange and green bars refer to the distribution obtained in the first and second peak, respectively, inferred by the model of Equation (
![]()
Figure 5.Deep-saturation distribution of  for the electrons extracted in a single cycle from the
for the electrons extracted in a single cycle from the  process (
process ( ,
,  corresponding to
corresponding to  ). The orange bars refer to the distribution obtained with the model of Equation (
). The orange bars refer to the distribution obtained with the model of Equation (
![]()
Figure 6.Average and rms residual momentum for the channel argon  , single pulse cycle with
, single pulse cycle with  , as a function of the pulse amplitude
, as a function of the pulse amplitude  . (a) Average momentum as expected by theory (blue line), by Monte Carlo simulations (red circles), by using the model of Equation (
. (a) Average momentum as expected by theory (blue line), by Monte Carlo simulations (red circles), by using the model of Equation ( function. The orange full-dashed line shows the analytical results without saturation effects, for reference. Red circles, blue triangles and green squares show the results by Monte Carlo, model and
function. The orange full-dashed line shows the analytical results without saturation effects, for reference. Red circles, blue triangles and green squares show the results by Monte Carlo, model and
The analytical estimation of the average and rms spread of momentum
The overall saturation correction slightly increases above unity in the range
3.3 Single-cycle, multiple-channel ionization processes
In the single-cycle intermediate and deep-saturation regimes, the pulse electric field is usually large enough to activate one (or more) ionization channel(s) above the starting, selected one. Referring to the usual argon example, when
The total number of extracted electrons in any peak can be obtained by solving the rate equations for the local available ions, namely:
Equations (27) very accurately predict the number of extracted electrons in any channel in a single pulse peak, being the maximum discrepancy between the inferred number of extracted electrons and Monte Carlo simulations outcomes below
![]()
Figure 8.Ionization fraction in the channels (0) and (1) as a function of the pulse amplitude for the case  ,
,  . The red lines refer to the predictions from Equation (
. The red lines refer to the predictions from Equation ( are obtained in this way.
are obtained in this way.
The distribution of the extracted electrons in the channel (0) follows the already discussed prescriptions from Equation (19). The distribution from process (1) originates both from the ions initially available at level (1) and from those that are freed while the phase proceeds within the peak. As the exact expression of the distribution,
The two-level model for the whole process occurring in a single peak, including the estimates of the extracted particles via Equation (27) and extraction phase distributions following the base-level distribution in Equations (19) and (29), can be combined so as to get the whole
In Figure 9(a), a blue line representing the average momentum as predicted by the single
![]()
Figure 9.Single-cycle, two-level ionization scan for the  process with
process with  . Red circles, blue diamonds and green squares refer to Monte Carlo simulations, model predictions and PIC simulations, respectively. (a) Average momentum from the two-level simulations and the model, as well as the average momentum as predicted by the single base level
. Red circles, blue diamonds and green squares refer to Monte Carlo simulations, model predictions and PIC simulations, respectively. (a) Average momentum from the two-level simulations and the model, as well as the average momentum as predicted by the single base level  , for reference (blue line). The vertical axis on the right shows the fraction of level (1) over the whole
, for reference (blue line). The vertical axis on the right shows the fraction of level (1) over the whole  particles extracted in the cycle. (b) rms momentum from the two-level simulations and the model. The blue line shows predictions by the theory of the base level without saturation effects on.
particles extracted in the cycle. (b) rms momentum from the two-level simulations and the model. The blue line shows predictions by the theory of the base level without saturation effects on.
4 Whole bunch emittance theory
As the cycle pulse amplitude depends on both the longitudinal and transverse coordinates, we make the substitution
4.1 Theory with negligible saturation effects
The description of the spatial dependence of
We stress that, depending upon the needed accuracy, it is possible to use either the expression containing the Euler incomplete Gamma functions or its (less accurate) polynomial expansion.
The longitudinal counterpart of Equation (33), that is,
The full average generator is finally evaluated as
![]()
Figure 10.Whole bunch rms momentum as a function of the normalized field strength  for a process without saturation and ponderomotive force effects. Diamond and circle points represent simulation results for krypton and argon, respectively. The orange and blue lines show, for the same processes, the analytical results from Equation (
for a process without saturation and ponderomotive force effects. Diamond and circle points represent simulation results for krypton and argon, respectively. The orange and blue lines show, for the same processes, the analytical results from Equation (
The functional generator of the moments
The gradient
A further average over the longitudinal
As a final result, as
Equations (42) and (43) correctly describe the whole-beam emittance in the case of negligible saturation, as is apparent in Figure 11(c), where the orange line matches with simulations relative to low values of
![]()
Figure 11.Bunch averaged normalized emittance obtained with a thin slice of ionizable atoms (either krypton or argon) with a scan of the normalized field strength  . The pulse wavelength, waist and duration are
. The pulse wavelength, waist and duration are  ,
,  and
and  , respectively. The emittance is further normalized by the pulse waist
, respectively. The emittance is further normalized by the pulse waist  and amplitude
and amplitude  , that is,
, that is,  . Here, black points represent the simulation results including ponderomotive force effects, while red points refer to simulations without ponderomotive force effects on. Diamond and circle points represent simulation results for krypton and argon, respectively, which include saturation effects during ionization but exclude the ponderomotive force contribution in the subsequent particle evolution. The dashed lines show, for the same processes, the analytical results excluding saturation effects. Thick lines show the analytical results with a full description of the ionization process.
. Here, black points represent the simulation results including ponderomotive force effects, while red points refer to simulations without ponderomotive force effects on. Diamond and circle points represent simulation results for krypton and argon, respectively, which include saturation effects during ionization but exclude the ponderomotive force contribution in the subsequent particle evolution. The dashed lines show, for the same processes, the analytical results excluding saturation effects. Thick lines show the analytical results with a full description of the ionization process.
4.2 Whole bunch quality including saturation effects
The onset of ionization saturation during the whole pulse passage usually occurs at pulse amplitudes close to those selected as working points, that is, lower than those necessary to get saturation effects within a single pulse peak. A first effect is the reduction of the number of particles extracted in the vicinity of the pulse axis, thus enhancing the statistical weight of the regions with
The integrated ionization weight
We can now use
The evaluation of the rms momentum including saturation effects proceeds by generalizing the generating function of the moments
where in the last manipulation we retained the lowest order in
Although the results from Equation (49) are strictly valid for
5 ReMPI injection simulation
The results reported in the previous sections do not take into account the effects of wakefield forces inducing the beam trapping (see Refs. [39,40] for the theory on ionization-induced injectors), which are also known to be potentially detrimental for transverse beam quality[41,42]. Although our theory is limited to the description of the phase-space just after the bunch slippage behind the laser pulse, it is interesting to compare the beam normalized emittance with the expected (minimum) value without wakefield effects and follow its evolution during the beam acceleration.
We selected a simple ReMPI configuration[18] with a driver train obtained by splitting a
A snapshot of the simulation results in the vicinity of the pulses foci is shown in Figure 12. As the train of pulses (polarized along
![]()
Figure 12.Simulation snapshot in the vicinity of the focus position. (a) Electron density, laser pulses transverse fields and longitudinal on-axis accelerating gradient. The envelopes of the driving pulses with carrier wavelength  are shown in orange, while the purple envelope refers to the frequency-doubled Ti:Sa laser constituting the ionizing pulse. A large amplitude wake is excited behind the second driver pulse, as is apparent from the longitudinal accelerating gradient (black line, a.u.). (b) On-axis transverse electric field of the driving train (black line), the ionizing pulse (purple) and the accelerating gradient (blue line). The fields are shown in a.u. with the correct ratio between the laser pulse amplitudes. The longitudinal phase-space plot of the extracted electrons with
are shown in orange, while the purple envelope refers to the frequency-doubled Ti:Sa laser constituting the ionizing pulse. A large amplitude wake is excited behind the second driver pulse, as is apparent from the longitudinal accelerating gradient (black line, a.u.). (b) On-axis transverse electric field of the driving train (black line), the ionizing pulse (purple) and the accelerating gradient (blue line). The fields are shown in a.u. with the correct ratio between the laser pulse amplitudes. The longitudinal phase-space plot of the extracted electrons with  is also shown. The inset shows the transverse phase-space cuts
is also shown. The inset shows the transverse phase-space cuts  and
and  .
.
![]()
Figure 13.Evolution of the normalized emittance along the ionization pulse polarization axis ( , blue) and along the driving pulse polarization (
, blue) and along the driving pulse polarization ( , orange). The green horizontal line refers to the expected emittance along
, orange). The green horizontal line refers to the expected emittance along  without the effect of the wakefield.
without the effect of the wakefield.
![]()
Figure 14.Snapshot at the end of the simulation. (a) On-axis transverse electric field of the driving train (black line), the ionizing pulse (purple) and the accelerating gradient (blue line). The longitudinal phase-space plot of the extracted electrons is also shown. The inset shows the transverse phase-space cuts  and
and  . (b) Slice analysis of the normalized emittance (blue line) and slice current (orange line). The dash-dotted line refers to the overall (i.e., projected) emittance, for reference.
. (b) Slice analysis of the normalized emittance (blue line) and slice current (orange line). The dash-dotted line refers to the overall (i.e., projected) emittance, for reference.
6 Summary
We reported on a comprehensive analysis of the 3D phase-space of the particles extracted via tunneling ionization by a single, linearly polarized, Gaussian laser pulse. Results concerning a single-cycle averaging showed that the model distribution of Equation (19) very accurately described the distribution of the momenta for a single ionization process (e.g.,
As a second outcome, we obtained a very accurate estimate of the whole bunch emittance, that is, the normalized emittance along the polarization axis of the electron bunch just after the pulse passage (see Equations (42) and (43) for the unsaturated case and Equations (48) and (49) for the saturated case). Our results for the whole bunch confirmed the emittance increase in the saturation regime as firstly reported in Ref. [31], improving the results shown there by giving analytical estimates of the rms transverse size increase and rms momentum slight decrease due to saturation effects.
The accuracy of the results reported in the manuscript has been checked either via full-PIC simulations or with ad hoc Monte Carlo codes, showing a remarkably high accuracy (with errors below 1%) of the analytical outcomes in the fully saturated regimes explored in the text. Our results, however, do not include the effect of the plasma wakefield where the extracted particles would be trapped. Also, transverse ponderomotive effects have not been taken into account in the analytical results concerning the transverse momentum and position separately, although their combination through the normalized emittance is not affected by the (leading term) radially linear ponderomotive force, as confirmed by our simulations.
Finally, we discussed the evolution of the beam emittance in a PIC simulation including the wakefield effects. The results concerning the whole-beam emittance we present here rely on the effect of the laser pulse solely, while wakefield transverse forces can induce emittance degradation either via the onset of nonlinear transverse forces or via phase mixing. We showed that, in the ReMPI (and also for a two-color) configuration, the possibility of generating very short bunches enables the possibility of limiting the emittance growth due to phase mixing, thus improving the final quality for a matched beam.
References
[1] T. Tajima, J. M. Dawson. Phys. Rev. Lett., 43, 267(1979).
[2] V. Malka, S. Fritzler, E. Lefebvre, M.-M. Aleonard, F. Burgy, J.-P. Chambaret, J.-F. Chemin, K. Krushelnick, G. Malka, S. P. D. Mangles, Z. Najmudin, M. Pittman, J.-P. Rousseau, J.-N. Scheurer, B. Walton, A. E. Dangor. Science, 298, 1596(2002).
[3] E. Esarey, C. B. Schroeder, W. P. Leemans. Rev. Mod. Phys., 81, 1229(2009).
[4] V. Malka. Phys. Plasmas, 19, 055501(2012).
[5] S. Bulanov, N. Naumova, F. Pegoraro, J. Sakai. Phys. Rev. E, 58, R5257(1998).
[6] H. Suk, N. Barov, J. B. Rosenzweig, E. Esarey. The Physics of High Brightness Beams(2000).
[7] T. Hosokai, K. Kinoshita, A. Zhidkov, K. Nakamura, T. Watanabe, T. Ueda, H. Kotaki, M. Kando, K. Nakajima, M. Uesaka. Phys. Rev. E, 67, 036407(2003).
[8] P. Tomassini, M. Galimberti, A. Giulietti, D. Giulietti, L. A. Gizzi, L. Labate, F. Pegoraro. Phys. Rev. ST Accel. Beams, 6, 121301(2003).
[9] K. Schmid, A. Buck, C. M. S. Sears, J. M. Mikhailova, R. Tautz, D. Herrmann, M. Geissler, F. Krausz, L. Veisz. Phys. Rev. ST Accel. Beams, 13, 091301(2010).
[10] A. Buck, J. Wenz, J. Xu, K. Khrennikov, K. Schmid, M. Heigoldt, J. M. Mikhailova, M. Geissler, B. Shen, F. Krausz, S. Karsch, L. Veisz. Phys. Rev. Lett., 110, 185006(2013).
[11] W. T. Wang, W. T. Li, J. S. Liu, Z. J. Zhang, R. Qi, C. H. Yu, J. Q. Liu, M. Fang, Z. Y. Qin, C. Wang, Y. Xu, F. X. Wu, Y. X. Leng, R. X. Li, Z. Z. Xu. Phys. Rev. Lett., 117, 124801(2016).
[12] K. K. Swanson, H.-E. Tsai, S. K. Barber, R. Lehe, H.-S. Mao, S. Steinke, J. van Tilborg, K. Nakamura, C. G. R. Geddes, C. B. Schroeder, E. Esarey, W. P. Leemans. Phys. Rev. Accel. Beams, 20, 051301(2017).
[13] J. Faure, C. Rechatin, A. Norlin, A. Lifschitz, Y. Glinec, V. Malka. Nature, 444, 737(2006).
[14] C. Rechatin, X. Davoine, A. Lifschitz, A. B. Ismail, J. Lim, E. Lefebvre, J. Faure, V. Malka. Phys. Rev. Lett., 103, 194804(2009).
[15] M. Hansson, B. Aurand, H. Ekerfelt, A. Persson, O. Lundh. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip., 829, 99(2016).
[16] L.-L. Yu, E. Esarey, C. B. Schroeder, J.-L. Vay, C. Benedetti, C. G. R. Geddes, M. Chen, W. P. Leemans. Phys. Rev. Lett., 112, 125001(2014).
[17] C. B. Schroeder, C. Benedetti, E. Esarey, M. Chen, W. P. Leemans. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip., 909, 149(2018).
[18] P. Tomassini, S. De Nicola, L. Labate, P. Londrillo, R. Fedele, D. Terzani, L. A. Gizzi. Phys. Plasmas, 24, 103120(2017).
[19] P. Tomassini, D. Terzani, F. Baffigi, F. Brandi, L. Fulgentini, P. Koester, L. Labate, D. Palla, L. A. Gizzi. Plasma Phys. Control. Fusion, 62, 014010(2019).
[20] P. Tomassini, D. Terzani, L. Labate, G. Toci, A. Chance, P. A. P. Nghiem, L. A. Gizzi. Phys. Rev. Accel. Beams, 22, 111302(2019).
[21] Y. Ma, D. Seipt, A. E. Hussein, S. Hakimi, N. F. Beier, S. B. Hansen, J. Hinojosa, A. Maksimchuk, J. Nees, K. Krushelnick, A. G. R. Thomas, F. Dollar. Phys. Rev. Lett., 124, 114801(2020).
[22] W. Wang, K. Feng, L. Ke, C. Yu, Y. Xu, R. Qi, Y. Chen, Z. Qin, Z. Zhang, M. Fang J. Liu, K. Jiang, H. Wang, C. Wang, X. Yang, F. Wu, Y. Leng, J. Liu, R. Li, Z. Xu. Nature, 595, 516(2021).
[23] R. W. Assmann, M. K. Weikum, T. Akhter, D. Alesini, A. S. Alexandrova, M. P. Anania, N. E. Andreev, I. Andriyash, M. Artioli, A. Aschikhin, T. Audet, A. Bacci, I. F. Barna, S. Bartocci, A. Bayramian, A. Beaton, A. Beck, M. Bellaveglia, A. Beluze, A. Bernhard, A. Biagioni, S. Bielawski, F. G. Bisesto, A. Bonatto, L. Boulton, F. Brandi, R. Brinkmann, F. Briquez, F. Brottier, E. Bründermann, M. Büscher, B. Buonomo, M. H. Bussmann, G. Bussolino, P. Campana, S. Cantarella, K. Cassou, A. Chancé, M. Chen, E. Chiadroni, A. Cianchi, F. Cioeta, J. A. Clarke, J. M. Cole, G. Costa, M.-E. Couprie, J. Cowley, M. Croia, B. Cros, P. A. Crump, R. D’Arcy, G. Dattoli, A. Del Dotto, N. Delerue, M. Del Franco, P. Delinikolas, S. De Nicola, J. M. Dias, D. Di Giovenale, M. Diomede, E. Di Pasquale, G. Di Pirro, G. Di Raddo, U. Dorda, A. C. Erlandson, K. Ertel, A. Esposito, F. Falcoz, A. Falone, R. Fedele, A. F. Pousa, M. Ferrario, F. Filippi, J. Fils, G. Fiore, R. Fiorito, R. A. Fonseca, G. Franzini, M. Galimberti, A. Gallo, T. C. Galvin, A. Ghaith, A. Ghigo, D. Giove, A. Giribono, L. A. Gizzi, F. J. Grüner, A. F. Habib, C. Haefner, T. Heinemann, A. Helm, B. Hidding, B. J. Holzer, S. M. Hooker, T. Hosokai, M. Hübner, M. Ibison, S. Incremona, A. Irman, F. Iungo, F. J. Jafarinia, O. Jakobsson, D. A. Jaroszynski, S. Jaster-Merz, C. Joshi, M. Kaluza, M. Kando, O. S. Karger, S. Karsch, E. Khazanov, D. Khikhlukha, M. Kirchen, G. Kirwan, C. Kitégi, A. Knetsch, D. Kocon, P. Koester, O. S. Kononenko, G. Korn, I. Kostyukov, K. O. Kruchinin, L. Labate, C. Le Blanc, C. Lechner, P. Lee, W. Leemans, A. Lehrach, X. Li, Y. Li, V. Libov, A. Lifschitz, C. A. Lindstrøm, V. Litvinenko, W. Lu, O. Lundh, A. R. Maier, V. Malka, G. G. Manahan, S. P. D. Mangles, A. Marcelli, B. Marchetti, O. Marcouillé, A. Marocchino, F. Marteau, A. M. de la Ossa, J. L. Martins, P. D. Mason, F. Massimo, F. Mathieu, G. Maynard, Z. Mazzotta, S. Mironov, A. Y. Molodozhentsev, S. Morante, A. Mosnier, A. Mostacci, A.-S. Müller, C. D. Murphy, Z. Najmudin, P. A. P. Nghiem, F. Nguyen, P. Niknejadi, A. Nutter, J. Osterhoff, D. O. Espinos, J.-L. Paillard, D. N. Papadopoulos, B. Patrizi, R. Pattathil, L. Pellegrino, A. Petralia, V. Petrillo, L. Piersanti, M. A. Pocsai, K. Poder, R. Pompili, L. Pribyl, D. Pugacheva, B. A. Reagan, J. Resta-Lopez, R. Ricci, S. Romeo, M. R. Conti, A. R. Rossi, R. Rossmanith, U. Rotundo, E. Roussel, L. Sabbatini, P. Santangelo, G. Sarri, L. Schaper, P. Scherkl, U. Schramm, C. B. Schroeder, J. Scifo, L. Serafini, G. Sharma, Z. M. Sheng, V. Shpakov, C. W. Siders, L. O. Silva, T. Silva, C. Simon, C. Simon-Boisson, U. Sinha, E. Sistrunk, A. Specka, T. M. Spinka, A. Stecchi, A. Stella, F. Stellato, M. J. V. Streeter, A. Sutherland, E. N. Svystun, D. Symes, C. Szwaj, G. E. Tauscher, D. Terzani, G. Toci, P. Tomassini, R. Torres, D. Ullmann, C. Vaccarezza, M. Valléau, M. Vannini, A. Vannozzi, S. Vescovi, J. M. Vieira, F. Villa, C.-G. Wahlström, R. Walczak, P. A. Walker, K. Wang, A. Welsch, C. P. Welsch, S. M. Weng, S. M. Wiggins, J. Wolfenden, G. Xia, M. Yabashi, H. Zhang, Y. Zhao, J. Zhu, A. Zigler. Eur. Phys. J. Spec. Topic, 229, 3675(2020).
[24] F. Albert, M.-E. Couprie, A. Debus, M. C. Downer, J. Faure, A. Flacco, L. A. Gizzi, T. Grismayer, A. Huebl, C. Joshi, M. Labat, W. P. Leemans, A. R. Maier, S. P. D. Mangles, P. Mason, F. Mathieu, P. Muggli, M. Nishiuchi, J. Osterhoff, P. P. Rajeev, U. Schramm, J. Schreiber, A. G. R. Thomas, J.-L. Vay, M. Vranic, K. Zeil. New J. Phys., 23, 2021(2020).
[25] P. Tomassini, A. R. Rossi. Plasma Phys. Control. Fusion, 58, 034001(2015).
[26] C. Benedetti, C. B. Schroeder, E. Esarey, C. G. R. Geddes, W. P. Leemans. AIP Conf. Proc., 1299, 250(2010).
[27] C. Benedetti, A. Sgattoni, G. Turchetti, P. Londrillo. IEEE Trans. Plasma Sci., 36, 1790(2008).
[28] D. Terzani, P. Londrillo. Comput. Phys. Commun., 242, 49(2019).
[29] J. Derouillat, A. Beck, F. Pérez, T. Vinci, M. Chiaramello, A. Grassi, M. Flé, G. Bouchard, I. Plotnikov, N. Aunai, J. Dargent, C. Riconda, M. Grech. Comput. Phys. Commun., 222, 351(2018).
[30] F. Massimo, A. Beck, J. Derouillat, I. Zemzemi, A. Specka. Phys. Rev. E, 102, 033204(2020).
[31] C. B. Schroeder, J.-L. Vay, E. Esarey, C. Benedetti, M. Chen, W. P. Leemans. Phys. Rev. ST Accel. Beams, 17, 101301(2014).
[32] D. Guénot, D. Gustas, A. Vernier, B. Beaurepaire, F. Böhle, M. Bocoum, M. Lozano, A. Jullien, R. Lopez-Martens, A. Lifschitz, J. Faure. Nat. Photonics, 11, 293(2017).
[33] J. Faure, D. Gustas, D. Guénot, A. Vernier, F. Böhle, M. Ouillé, S. Haessler, R. Lopez-Martens, A. Lifschitz. Plasma Phys. Control. Fusion, 61, 014012(2018).
[34] A. F. Lifschitz, V. Malka. New J. Phys., 14, 053045(2012).
[35] A. M. Perelomov, V. S. Popov, M. V. Terent’ev. Soviet J. Exp. Theor. Phys, 23, 924(1966).
[36] M. V. Ammosov, N. B. Delone, V. P. Krainov.
[37] G. L. Yudin, M. Y. Ivanov. Phys. Rev. A, 64, 013409(2001).
[38] R. Nuter, L. Gremillet, E. Lefebvre, A. Lévy, T. Ceccotti, P. Martin. Phys. Plasmas, 18, 033107(2011).
[39] M. Chen, E. Esarey, C. B. Schroeder, C. G. R. Geddes, W. P. Leemans. Phys. Plasmas, 19, 033101(2012).
[40] A. Zhidkov, N. Pathak, J. K. Koga, K. Huang, M. Kando, T. Hosokai. Phys. Rev. Res., 2, 013216(2020).
[41] J. J. Su, T. Katsouleas, J. M. Dawson, R. Fedele. Phys. Rev. A, 41, 3321(1990).
[42] X. L. Xu, J. F. Hua, F. Li, C. J. Zhang, L. X. Yan, Y. C. Du, W. H. Huang, H. B. Chen, C. X. Tang, W. Lu P. Yu, W. An, C. Joshi, W. B. Mori. Phys. Rev. Lett., 112, 035003(2014).
[43] R. Lehe, M. Kirchen, I. A. Andriyash, B. B. Godfrey, J.-L. Vay. Comput. Phys. Commun., 203, 66(2016).
[44] E. Esarey, P. Sprangle, J. Krall, A. Ting, G. Joyce. Phys. Fluids B, 5, 2690(1993).
[45] A. Pak, S. F. Martins, W. Lu, W. B. Mori, C. Joshi. Phys. Rev. Lett., 104, 025003(2010).
[46] A. Beck, J. Derouillat, M. Lobet, A. Farjallah, F. Massimo, I. Zemzemi, F. Perez, T. Vinci, M. Grech. Comput. Phys. Commun., 244, 246(2019).
[47] A. Lifschitz, X. Davoine, E. Lefebvre, J. Faure, C. Rechatin, V. Malka. J. Comput. Phys., 228, 1803(2008).
[48] I. Zemzemi, F. Massimo, A. Beck. J. Phys. Conf. Ser., 012054(2020).
[49] I. Zemzemi. , “High-performance computing and numerical simulation for laser wakefield acceleration with realistic laser profiles,” Theses (Institut Polytechnique de Paris, ).(2020).
[50] B. Quesnel, P. Mora. Phys. Rev. E, 58, 3719(1998).

Set citation alerts for the article
Please enter your email address



