- High Power Laser Science and Engineering
- Vol. 11, Issue 2, 02000e28 (2023)
Abstract
Keywords
1 Introduction
The propagation of a high-power laser pulse in a medium with cubic nonlinearity entails a number of physical effects. Many of them are used to control beam parameters: self-phase modulation for white light generation[1], post-compression of femtosecond pulses[2–4] and pulse amplitude and phase characterization[5,6]; generation of a cross-polarized beam[7]; rotation of a polarization ellipse[8,9]; nonlinear phase shift used for the enhancement of the temporal contrast of a pulse[10,11]; self-focusing of a beam as a whole for mode locking[12]. At the same time, cubic nonlinearity gives rise to destructive effects, which limit the propagation length of high-power laser pulses in optical materials. For example, when a laser pulse is propagating in fibers and capillaries, self-focusing of the beam as a whole limits the pulse power[3], and at second harmonic generation (SHG) self-phase modulation leads to degradation of the phase-matching condition[13,14].
However, the most significant detrimental effect is small-scale self-focusing (SSSF) occurring in bulk optics, which leads to beam filamentation. This significantly degrades the beam quality and eventually, in most cases, leads to optical breakdown. SSSF is the spatial instability of a plane wave propagating in a medium with cubic nonlinearity – the amplification of transverse spatial perturbations (noise)[15]. The first experimental observation[16] showed a quantitative agreement with the predictions[15]. This stationary theory (i.e., related to the instability of a strong monochromatic plane wave) has been developed in a great variety of works (many of them are referenced in Ref. [17] and, to name a few, the pioneering papers in Refs. [18–20]).
The key conclusion is that the SSSF instability occurs in the
Sign up for High Power Laser Science and Engineering TOC. Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
The noise power gain is as follows:
which is defined as the gain of noise spatial harmonic intensity at spatial frequency
where
where
The straightforward extension of this theory (which describes the spatial instability of a plane wave) to high-power optical pulses can be derived assuming time
This approach, which we refer to as stationary, is apparently well justified for nanosecond pulses but rather debatable for much shorter pulses, for example, for the tens of femtoseconds range. As opposed to the stationary approach, the solution of equations that describes the propagation of a short intense laser pulse in a nonlinear dispersive medium hereinafter will be called a nonstationary theory and will be discussed in Section 2.
Thus, SSSF development is determined, on the one hand, by the noise power and its spatial spectrum at the input to the medium and, on the other hand, by the nonlinearity the measure of which is the B-integral. A large number of experiments with nanosecond pulses showed that the influence of input noise is actually not essential, since the spatial noise cannot be completely eliminated anyway and for the most dangerous angles
1.1 The reduction of noise power at the input to the nonlinear medium
For nanosecond lasers, a typical beam intensity is several
The first of them is spatial self-filtering of the beam during propagation in free space[32]. If the nonlinear medium is rather far away from the noise source (NS; which is in most cases any optical surface touched by the beam), then the most ‘hazardous’ noise transverse spatial frequency
1.2 Substantial reduction of noise gain for short pulses
The spatiotemporal instability of a plane wave in the approximation of a slowly varying amplitude was investigated in Ref. [37] and an expression for the instability increment taking into account higher-order dispersions, spatiotemporal focusing (the nonstationary diffraction term) and self-steepening was obtained in Ref. [38]. Analytical expressions for the noise power gain similar to Equation (2) cannot be obtained. In Refs. [39,40], the development of SSSF was studied without the approximation of slowly varying amplitude. It was shown numerically that, in the case of anomalous dispersion, SSSF does not develop for laser pulses with a duration of less than 10 field periods. Experimental confirmation of this effect has not been demonstrated. Moreover, with normal dispersion, this effect has not been studied either theoretically or in simulation.
In Section 2 of this work we perform a detailed analysis of noise gain at nonstationary nonlinear interaction and determine the parameters at which SSSF is suppressed. Results of the measurements of spatial noise gain and their comparison with the stationary theory (Equation (4)) and numerical simulation of the nonstationary problem considered in Section 2 are presented in Section 3.
2 Numerical simulation
The numerical simulation of SSSF was performed using two approaches. The first one is based on the slowly varying amplitude approximation that gives a modified nonlinear Schrödinger equation (NSE) for a complex field amplitude
where
where
The second approach proposed in Refs. [42–44] is based on the unidirectional wave equation (UWE) for a complete oscillating optical complex field
Third- and higher-order dispersions as well as the third harmonic generation are already neglected in the NSE (Equation (6)). The UWE (Equation (9)) intrinsically contains second and third dispersion orders. Using the same definition (Equation (8)) one can obtain
From Equations (6) and (9) it is clear that the nonstationary problem depends, besides the B-integral (Equation (3)), on two dimensionless parameters,
Instead of
Parameter
Both Equations (6) and (9) were solved numerically for identical parameters and boundary conditions. An intense pulse with uniform spatial distribution combined with weak spatial noise with the same temporal shape was fed to the nonlinear medium input (
where
We restricted the consideration to the linear regime, when the noise growth had no back-action on the strong pulse. For this, the noise amplitude was chosen so small that even at the output of the nonlinear medium it stayed much smaller than the amplitude of the strong pulse. The field of the strong wave at the input
The results of numerical simulation showed that Equations (6) and (9) give similar results. The solid curves for
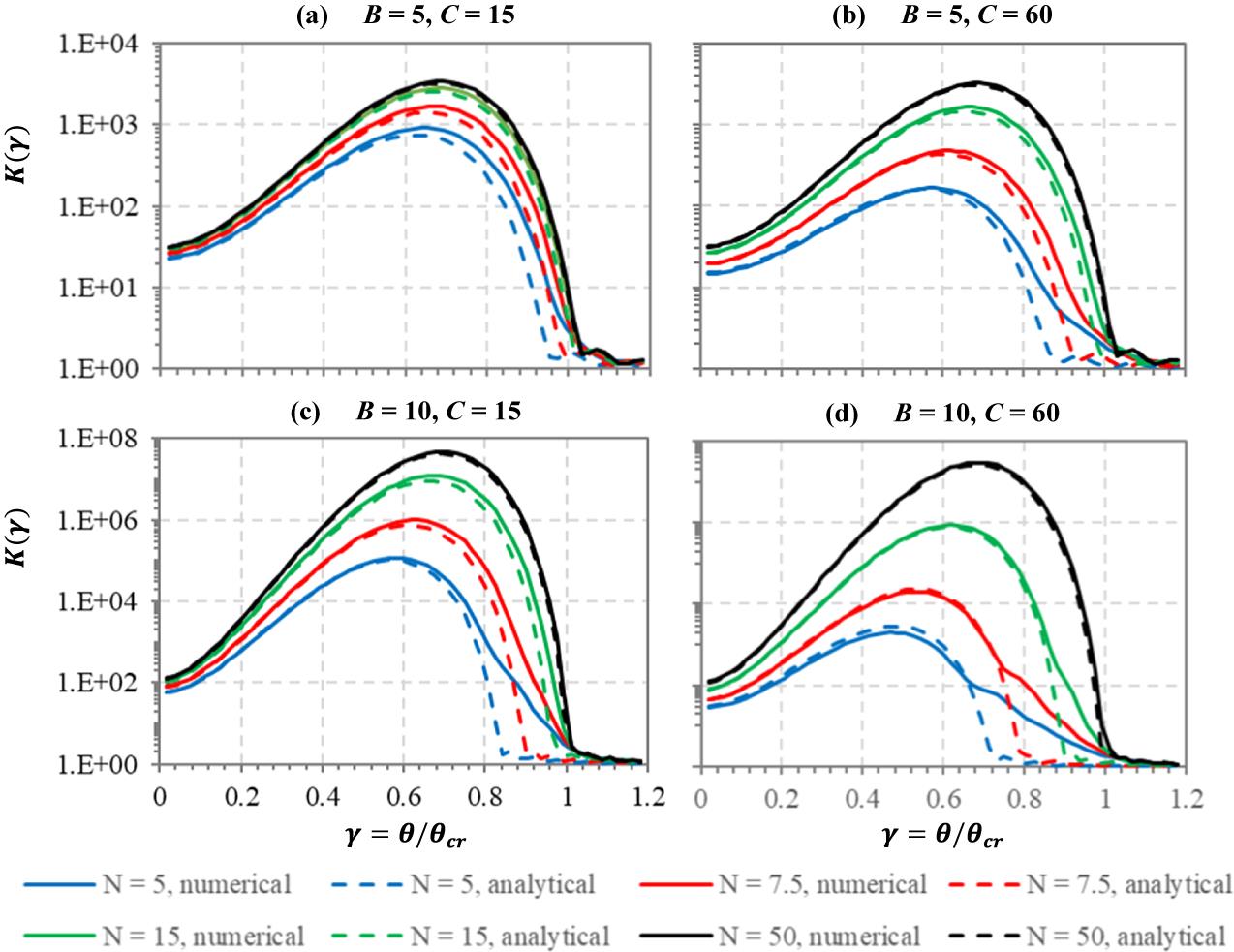
Figure 1.Gain  as a function of
as a function of  for
for  (a), (c) and
(a), (c) and  (b), (d);
(b), (d);  (a), (b) and
(a), (b) and  (c), (d); for
(c), (d); for  (black curves),
(black curves),  (green curves),
(green curves),  (red curves) and
(red curves) and  (blue curves). The solid curves show the results of numerical simulation, while the dashed curves are plotted by
(blue curves). The solid curves show the results of numerical simulation, while the dashed curves are plotted by  replaced by
replaced by  .
.
where the intensity
Using the results obtained in Ref. [45], it can be easily shown that the durations of the input and output pulses practically do not differ if
3 Experimental results and discussion
The experimental layout is shown in Figure 2. A beam of the laser PEARL (PEtawatt pARametric Laser[46]) with central wavelength 910 nm, pulse energy up to 17 J, full width at half maximum (FWHM) pulse duration 65 fs (N = 13) and diameter 18 cm passed through an orifice with a diameter of 10 cm located in vacuum at a distance of 8 m from the last compressor grating. The purpose of the orifice was to trim out the lateral wings of the beam to make the residual central part more like a flat-top for better interpretation of the results. The intensity averaged across the nearly flat-top beam was 0.8
![]()
Figure 2.Experimental layout. NS – noise source (randomly scratched 0.5 mm thick glass plate), NLP – nonlinear plate (BK7 glass or KDP), PHM – mirror with a pinhole.
First of all, the NS scratch density was chosen such that most of the noise was introduced by the NS, whereas the noise from the other optical elements located both upstream and downstream of the NLP could be neglected (comparing the black and green curves in Figure 3(a)). These measurements were made in a linear regime with
![]()
Figure 3.Experimental noise spectra (a) and noise gain  (b).
(b).
A small modulation of the function
Thus, the experimental results demonstrate significant suppression of SSSF at
4 Conclusion
The detailed numerical simulation of the propagation of femtosecond laser pulses in a medium with Kerr nonlinearity showed that, in the case of normal dispersion (in contrast to anomalous dispersion[39,40]), SSSF is not suppressed. Even for short laser pulses, noise gain is well described by the stationary theory (Equations (2) and (4)) if the B-integral (Equation (3)) is replaced by
References
[1] A. Dubietis, G. Tamošauskas, R. Šuminas, V. Jukna, A. Couairon. Lith. J. Phys., 57(2017).
[2] M. Hanna, F. Guichard, N. Daher, Q. Bournet, X. Délen, P. Georges. Laser Photon. Rev., 15, 2100220(2021).
[3] T. Nagy, P. Simon, L. Veisz. Adv. Phys. X, 6, 1845795(2020).
[4] E. A. Khazanov, S. Y. Mironov, G. Mourou. Uspekhi Fizicheskih Nauk, 189, 1173(2019).
[5] E. A. Anashkina, V. N. Ginzburg, A. A. Kochetkov, I. V. Yakovlev, A. V. Kim, E. A. Khazanov. Sci. Rep., 6, 33749(2016).
[6] A. V. Andrianov, A. V. Kim, E. A. Khazanov. Quantum Electron., 47, 236(2017).
[7] A. Jullien, O. Albert, F. Burgy, G. Hamoniaux, J.-P. Rousseau, J.-P. Chambaret, F. Augé-Rochereau, G. Chériaux, J. Etchepare, N. Minkovski, S. M. Saltiel. Opt. Lett., 30, 920(2005).
[8] K. Sala, M. C. Richardson. J. Appl. Phys., 49, 2268(1978).
[9] N. G. Khodakovskiy, M. P. Kalashnikov, V. Pajer, A. Blumenstein, P. Simon, M. M. Toktamis, M. Lozano, B. Mercier, Z. Cheng, T. Nagy, R. Lopez-Martens. Laser Phys. Lett., 16, 095001(2019).
[10] E. Khazanov. Opt. Express, 29, 17277(2021).
[11] D. Silin, E. Khazanov. Opt. Express, 30, 4930(2022).
[12] D. E. Spence, P. N. Kean, W. Sibbett. Opt. Lett., 16, 42(1991).
[13] T. Ditmire, A. M. Rubenchik, D. Eimerl, M. D. Perry. J. Opt. Soc. Am. B, 13, 649(1996).
[14] S. Y. Mironov, V. N. Ginzburg, V. V. Lozhkarev, G. A. Luchinin, A. V. Kirsanov, I. V. Yakovlev, E. A. Khazanov, A. A. Shaykin. Quantum Electron., 41, 963(2011).
[15] V. I. Bespalov, V. I. Talanov. JETP Lett., 3, 471(1966).
[16] Y. S. Chilingarian. JETP, 55, 1589(1968).
[17] A. J. CampilloSelf-focusing: Past and Present, 157(2009).
[18] B. Suydam. IEEE J. Quantum Electron., 10, 837(1974).
[19] C. Elliott, B. Suydam. IEEE J. Quantum Electron., 11, 863(1975).
[20] N. N. Rosanov, V. A. Smirnov. Soviet J. Quantum Electron., 10, 232(1980).
[21] A. K. Potemkin, E. A. Khazanov, M. A. Martyanov, M. S. Kochetkova. IEEE J. Quantum Electron., 45, 336(2009).
[22] G. Mourou, G. Cheriaux, C. Radier. , , and , “Device for generating a short duration laser pulse.” Patent US20110299152A1 (2014-08-05)..
[23] S. N. Vlasov, E. V. Koposova, V. E. Yashin. Quantum Electron., 42, 989(2012).
[24] A. A. Mak, V. E. Yashin. Opt. Spectrosc., 70, 1(1991).
[25] A. A. Andreev, A. A. Mak, V. E. Yashin. Quantum Electron., 27, 95(1997).
[26] S. Mironov, V. Lozhkarev, G. Luchinin, A. Shaykin, E. Khazanov. Appl. Phys. B, 113, 147(2013).
[27] A. Shaykin, V. Ginzburg, I. Yakovlev, A. Kochetkov, A. Kuzmin, S. Mironov, I. Shaikin, S. Stukachev, V. Lozhkarev, A. Prokhorov, E. Khazanov. High Power Laser Sci. Eng, 9, e54(2021).
[28] V. Ginzburg, I. Yakovlev, A. Kochetkov, A. Kuzmin, S. Mironov, I. Shaikin, A. Shaykin, E. Khazanov. Opt. Express, 29, 28297(2021).
[29] V. Ginzburg, I. Yakovlev, A. Zuev, A. Korobeynikova, A. Kochetkov, A. Kuzmin, S. Mironov, A. Shaykin, I. Shaikin, E. Khazanov, G. Mourou. Phys. Rev. A, 101, 013829(2020).
[30] V. N. Ginzburg, I. V. Yakovlev, A. S. Zuev, A. P. Korobeynikova, A. A. Kochetkov, A. A. Kuzmin, S. Yu. Mironov, A. A. Shaykin, I. A. Shaikin, E. A. Khazanov. Quantum Electron., 50, 331(2020).
[31] P. Lassonde, S. Mironov, S. Fourmaux, S. Payeur, E. Khazanov, A. Sergeev, J.-C. Kieffer, G. Mourou. Laser Phys. Lett., 13, 075401(2016).
[32] S. Y. Mironov, V. V. Lozhkarev, V. N. Ginzburg, I. V. Yakovlev, G. Luchinin, A. Shaykin, E. A. Khazanov, A. Babin, E. Novikov, S. Fadeev, A. M. Sergeev, G. A. Mourou. IEEE J. Select. Top. Quantum Electron., 18, 7(2012).
[33] J. I. Kim, Y. G. Kim, J. M. Yang, J. W. Yoon, J. H. Sung, S. K. Lee, C. H. Nam. Opt. Express, 30, 8734(2022).
[34] V. N. Ginzburg, A. A. Kochetkov, A. K. Potemkin, E. A. Khazanov. Quantum Electron., 48, 325(2018).
[35] E. A. Khazanov. Quantum Electron., 52, 208(2022).
[36] V. N. Ginzburg, A. A. Kochetkov, S. Y. Mironov, A. K. Poteomkin, D. E. Silin, E. A. Khazanov. Izv. VUZov. Radiofizika, 62, 953(2019).
[37] A. G. Litvak, V. I. Talanov. Izv. VUZov. Radiofizika, 10, 539(1967).
[38] L. Bergé, S. Mauger, S. Skupin. Phys. Rev. A, 81, 013817(2010).
[39] A. A. Balakin, A. V. Kim, A. G. Litvak, V. A. Mironov, S. A. Skobelev. Phys. Rev. A, 94, 043812(2016).
[40] A. A. Balakin, A. G. Litvak, V. A. Mironov, S. A. Skobelev. J. Opt., 19, 095503(2017).
[41] T. Brabec, F. Krausz. Phys. Rev. Lett., 78, 3282(1997).
[42] V. G. Bespalov, S. A. Kozlov, Y. A. Shpolyanskiy, I. A. Walmsley. Phys. Rev. A, 66, 013811(2002).
[43] A. A. Balakin, A. G. Litvak, V. A. Mironov, S. A. Skobelev. Phys. Rev. A, 78, 061803(2008).
[44] A. A. Balakin, A. G. Litvak, V. A. Mironov, S. A. Skobelev. Phys. Rev. A, 80, 063807(2009).
[45] A. Zheltikov. Opt. Express, 26, 17571(2018).
[46] V. V. Lozhkarev, G. I. Freidman, V. N. Ginzburg, E. V. Katin, E. A. Khazanov, A. V. Kirsanov, G. A. Luchinin, A. N. Mal’shakov, M. A. Martyanov, O. V. Palashov, A. K. Poteomkin, A. M. Sergeev, A. A. Shaykin, I. V. Yakovlev. Laser Phys. Lett., 4, 421(2007).

Set citation alerts for the article
Please enter your email address



