Single-cavity bi-color laser enabled by optical anti-parity-time symmetry

Yao Duan; Xingwang Zhang; Yimin Ding; Xingjie Ni

doi:10.1364/PRJ.417296

Abstract

The exploration of quantum inspired symmetries in optical systems has spawned promising physics and provided fertile ground for developing devices exhibiting exotic functionalities. Founded on the anti-parity–time (APT) symmetry that is enabled by both spatial and temporal interplay between gain and loss, we demonstrate theoretically and numerically bi-color lasing in a single micro-ring resonator with spatiotemporal modulation along its azimuthal direction. In contrast to conventional multi-mode lasers that have mixed-frequency output, our laser exhibits stable, demultiplexed, tunable bi-color emission at different output ports. Our APT-symmetry-based laser may point out a new route for realizing compact on-chip coherent multi-color light sources.

Recently, the exploration of non-Hermitian quantum symmetries, especially parity–time (PT) symmetry in photonic systems has enabled new features and functionalities in laser systems [12,13]. Compared with other approaches that mainly rely on varying refractive indices to tune cavity resonances, non-Hermitian symmetry-based optical systems are based on the modulation of gain and loss, i.e., the part of a refractive index to manipulate the imaginary part of resonances. The peculiarity of PT-symmetry-induced properties have led to the development of new laser systems, such as loss-induced revival of lasing [14], alleviation of mode competition [15], and lasing wavefront shaping [16,17]. However, current reported PT symmetric lasers distribute gain and loss only in the spatial dimension. This spatial degree of freedom has limited control over the coupling among modes with the same frequency. It does not have the capability to control mode coupling in the frequency domain, which is essential for achieving controllable multi-color lasing in a single cavity.

Here we propose a new scheme for creating a single-cavity multi-color laser by engineering gain and loss in both spatial and temporal domains based on the concept of anti-PT (APT) symmetry. As a demonstration, we design and numerically simulate a micro-ring bi-color laser with realistic physical parameters. The stabilized and tunable bi-color emission is protected by the modulation wavevector and modulation frequency. Moreover, as the laser emission is originated from two counter-propagating modes in the micro-ring cavity, the two frequency outputs are well separated and can be used independently. We believe that this APT-symmetry-enabled bi-color lasing scheme provides a brand new route towards compact on-chip multi-color lasers, which could be promising coherent sources for future photonic integrated chips.

Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you！Sign up now

[\hat{H}, \hat{P} \hat{T}] = 0

{\hat{H}}^{(APT)} = i {\hat{H}}^{(PT)}

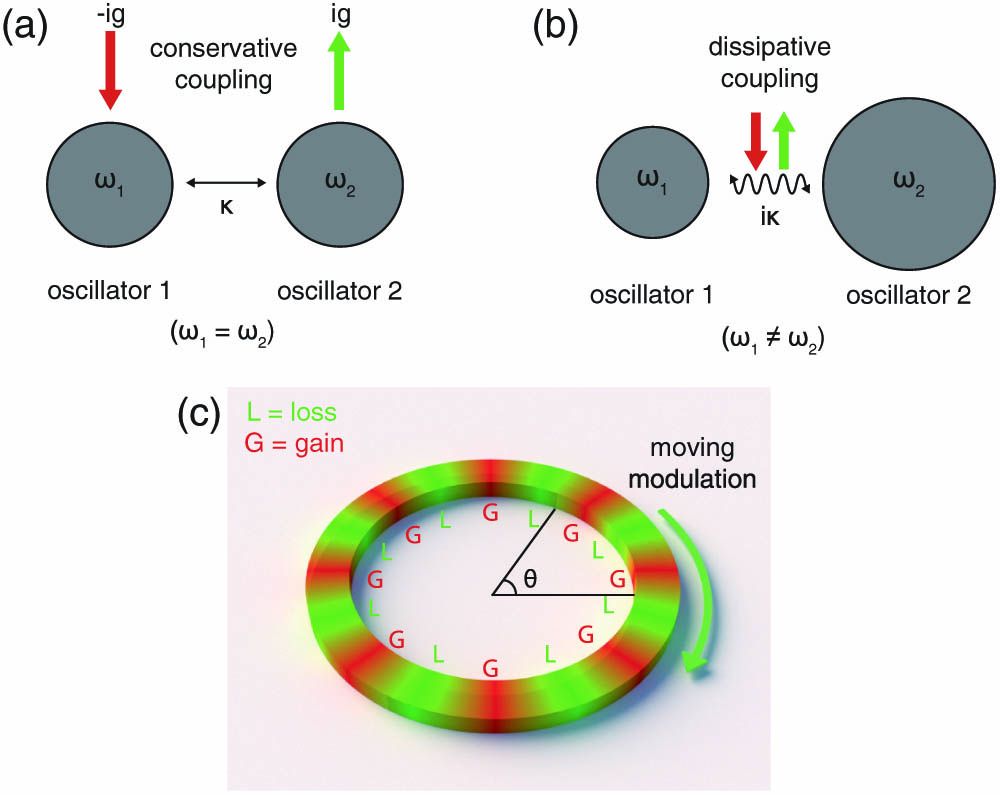
Figure 1.Schematic illustration of (a) PT and (b) APT symmetries in a two-oscillator system.

- i g

(ig) and

κ

represent gain (loss) and coupling coefficients, respectively. In the PT symmetric system, resonance frequencies

ω_{1}

ω_{2}

of the two oscillators are identical, while they are different in the APT symmetric one. (c) Configuration of APT symmetric micro-ring resonator under spatiotemporal modulation for bi-color lasing. The dynamic imaginary grating of permittivity with alternating gain (G) and loss (L) is moving azimuthally along the ring. The moving direction is indicated by the green arrow.

\hat{H} (t) Ψ (t) = i \frac{d Ψ (t)}{d t},

a_{1}

ω_{1, 2}

ω_{1, 2} + ω_{m} / 2

{\hat{H}, \hat{P} \hat{T}} = 0

ω_{1, 2} + ω_{m} / 2

Figure 2.(a) Real and (b) imaginary parts of normalized eigenfrequency spectra with respect to modulation frequency

ω_{m}

and coupling coefficient

κ_{m}

. The black dashed lines are the exceptional lines, where the two eigenstates degenerate. (c) Real (solid lines) and imaginary parts (dashed lines) of eigenfrequencies under a fixed

κ_{m}

indicated by the gray planes in (a) and (b), respectively. The yellow and red regions indicate broken APT and unbroken APT phases, respectively. (d) Real and (e) imaginary parts of the eigenfrequencies versus

κ_{m}

with different

ω_{m}

(indicated by different colors). The red circles in (d) indicate the uncoupled cases (

κ_{m} = 0

), and there are no sidebands. The red and blue curves are the modes in a PT symmetric case as reported in Ref. [15] for reference.

κ_{m} > | ω_{m} | / 2

\pm ω_{m} / 2

κ_{m}

| \pm l ⟩

Figure 3.(a) Normalized reflection spectra

T_{11}

and lasing spectra

T_{1}

, (b) normalized transmission spectra

T_{21}

and lasing spectra

T_{2}

under different modulation depths

Δ ϵ_{I}

with a fixed modulation frequency

ω_{m} = 1 THz

(see Fig. 6 in Appendix B for

T_{31}

and

T_{41}

). The definitions of the ports,

T_{11}

T_{21}

T_{1}

, and

T_{2}

are depicted in the insets. The yellow and red regimes indicate the broken and unbroken APT phases, respectively. (c) Real parts of the resonance frequencies and (d) imaginary parts of resonance wave vectors extracted from full-wave simulations (circles) and theoretical calculations based on the APT symmetry (dashed lines). The colors of the dashed curves in (c) and (d) correspond to the lines of the same color in (a) and (b).

Δ ϵ_{I}

{β^{'}}^{'}

ω_{m}

Figure 4.Normalized intensity distribution of the micro-ring system at (a)

λ = 1.552 μm

and (b)

λ = 1.560 μm

with

Δ ϵ_{I} = 0.508

and

ω_{m} = 1 THz

. The white lines outline the geometry of the micro-ring as well as the coupling waveguides. The white arrows indicate the traveling direction of spatiotemporal modulation, and the yellow arrows show the output lasing direction. The ports are numbered in the same way as those shown in Fig. 3. (c) Real parts of resonance frequencies extracted from full-wave simulations (circles) and the calculated ones based on our APT theory (dashed lines) with a fixed

Δ ϵ_{I} = 0.315

while varying

ω_{m}

. The red regime indicates the unbroken APT phase. (d) Lasing spectra from all ports with the same modulation depth as in (a) and (b).

l

is the azimuthal order of the WGM.

| \pm 21 ⟩

T_{21}

In conclusion, we theoretically proposed and numerically validated an APT symmetric bi-color laser enabled by spatiotemporal modulation of gain/loss distribution in a micro-ring resonator. Tunable modulation frequency and modulation depth provide two degrees of freedom for real-time manipulation of the lasing dynamics. This APT-symmetry-enabled bi-color lasing scheme can be generalized to multi-color cases with more than two lasing modes. Exploiting the non-Hermitian symmetries in optical systems, we can expect the revolution of current lasers in terms of functionality, stability, size, etc., which could enable a plethora of applications such as on-chip coherent light sources for communications, remote sensing, and displays.

The micro-ring bi-color laser model with dynamic modulation was established in Lumerical FDTD software. The time-varying permittivity was realized by a customized material plug-in. Compared with modulation of the real part of permittivity, manipulation of only the imaginary part was difficult since we could not directly assign an imaginary number to variables in the material plug-in. A viable way is to use the Lorentz model with well-tuned parameters. Therefore, the modulation of permittivity

Δ ?_{m}

can be written as

Δ ?_{m} (t, ?) = \frac{ω_{0 m}^{2}}{ω_{0 m}^{2} ? 2 i Γ_{m} ω ? ω^{2}} ? \cos (ω_{m} t ? L_{m} ?) Δ ? .

(A1)

Here

ω_{0 m}

is the center resonance frequency, and

Γ_{m}

is the damping coefficient of the material.

ω

is the frequency of a wave traveling through the medium, and

ω_{m}

L_{m}

?

are modulation frequency, modulation wave vector, and modulation phase, respectively.

Δ ?

is the modulation depth that we can tune during simulation. To get almost a pure imaginary part modulation, we first set

ω_{0 m}

around the scale of simulation frequency (

> 100 ?? THz

for 1.555?μm) and

Γ_{m} ? ω_{0 m}

. However, the simulation process was quite unstable, and no dynamic modulation effect was observed if

Γ_{m} {> 10}^{16} ?? s^{? 1}

. Therefore, we reduced

Γ_{m}

and kept it slightly larger than

ω_{0 m}

with

ω_{0 m} = 1.215 \times 10^{15} ?? s^{? 1}

and

Γ_{m} = 3.5 \times 10^{15} ?? s^{? 1}

. With

Δ ? ? \cos (ω_{m} t ? L_{m} ?) = 1

, the time-independent

Δ ?_{m}

around 1.55?μm is shown in Fig.?5. The imaginary part is almost 100 times larger than the real part, which can approximately be viewed as the modulation of the imaginary part only. But the influence of a tiny residue real part modulation on eigenmode frequencies cannot be fully eliminated, which is manifested as small but persistent drift of all resonance curves under increasing modulation depth, as shown in Figs.?3(a)–3(c).

Figure 5.Real and imaginary parts of

Δ ϵ_{m}

around 1.55 μm under

ω_{0 m} = 1.215 \times 10^{15} s^{- 1}

and

Γ_{m} = 3.5 \times 10^{15} s^{- 1}

. The imaginary part is around 100 times larger than the real part.

The theoretical prediction deviated a little bit from the simulation result when

Δ ?_{I} < 0.135

(Fig.?3), because there was competition between the dynamic coupling and static backscattering process induced by the simulation grid. The static backscattering was weak but dominant when the modulation was small, which would shift the resonances slightly.

In Figs.?6(a) and 6(b), we also notice that the second resonance cannot be observed in

T_{41}

, while

T_{31}

looks almost the same as in Fig.?3(a). Since we used a short input pulse whose length was less than the perimeter of the ring in the simulation, the field was unevenly distributed inside the ring. The sideband did not get much energy converted from the main resonance owing to a short propagation length in the first half-cycle along the ring. The energy coupled out into the drop waveguide was very small. Then the sideband accumulated enough energy from the last half-cycle but most was coupled out into the input bus waveguide. Therefore, we could see a sideband peak in

T_{21}

but not in

T_{41}

Figure 6.(a) Numerical normalized transmission spectra

T_{31}

, lasing spectra

T_{3}

, (b) transmission spectra

T_{41}

, and lasing spectra

T_{4}

under different modulation depths

Δ ϵ_{I}

and

ω_{m} = 1 THz

. The definitions of

T_{31}

T_{41}

T_{3}

, and

T_{4}

are depicted in the inset. The yellow and red shaded areas indicate different APT phases.

Figures?3 and 6 show the reflection and transmission spectra over different modulation depths. Based on Eq.?(4), increasing the modulation frequency from zero will result in the phase transition from unbroken APT phase to broken APT phase. This trend can be verified in Figs.?4 and 7. In Fig.?7, all the spectra start from one lasing peak and bifurcate into two converging resonance peaks (or dips) under increasing

ω_{m}

. The frequency difference between two resonances increases with larger

ω_{m}

. At the same time, the amplitude of the second resonance reduces owing to the deviation from the center frequency of the original WGM resonance, which will result in a larger phase mismatch. If we record the resonance position and plot the dependence of resonance wavelength with

ω_{m}

, they also fit well with APT theory as in Fig.?4(c).

Figure 7.Simulated transmission spectra from

T_{11}

T_{41}

and lasing spectra from

T_{1}

T_{4}

under increasing modulation frequency. Modulation depth

Δ ϵ = 0.315

. The circles mark the spectral position of the resonances. The red regime indicates unbroken APT phase.

To apply spatiotemporal modulation on the micro-ring in simulation, the assumption of continuous modulation can be approximated only by discretized blocks. The permittivity of these blocks differs coherently by a fixed phase shift along the ring to represent the spatial variation. If the ring is discretized into

N

blocks in total along the ring, the modulation can be expressed as

?_{eff} (?, t) = Δ ?_{m} \sum_{n = 1}^{N} \cos (ω_{m} t ? L_{m} ?_{n}) rect (\frac{? ? ?_{n}}{Δ ?}),

(D1)

where

rect (x)

is a rectangular function with unitary height and width centered at zero.

Δ ?_{m}

is modulation strength.

ω_{m}

t

L_{m}

, and

?_{n}

have the same definition as in Eq.?(A1).

Δ ? = 2 π / N

is the angular width of a single block, and

?_{n} = (n ? 1 / 2) Δ ?

is the angular position of the center of the

n

th block. Based on Poisson summation, it can be expanded as [33]

?_{eff} (?, t) = Δ ?_{m} \sum_{k = ? \infty}^{\infty} {(? 1)}^{k (N ? 1)} sinc (\frac{L_{m} + k N}{N}) ? \cos [ω_{m} t ? (L_{m} + k N) ?],

(D2)

where

sinc (x) = \sin (π x) / (π x)

, and

k

is an integer. Therefore, a discretized stepwise permittivity profile can be decomposed into a combination of sinusoidal modulation with the same modulation frequency but different wave vectors. Considering the phase match condition, only the one satisfying

L_{m} + k N = 2 l

can resonantly introduce dynamic coupling between

| \pm l ?

. The effective modulation depth can be computed as

Δ ?_{eff} = Δ ?_{m} sinc (\frac{2 l}{N}) .

(D3)

In our simulation,

N = 100

l = 21

, with

k = 0

L_{m} = 2 l

, and

Δ ?_{eff} = 0.7341 Δ ?_{m}

. Moreover, the actual modulation depth of the imaginary part should also consider the modulation depth of the Lorentz model in the material plug-in, which is

Δ ?_{m} = 0.173 Δ ?

around 1.55?μm. Considering all of these, we can get

Δ ?_{eff} = 0.127 Δ ?

. Therefore, the sinusoidal modulation can be well approximated by a stepwise modulation model that differs only by a constant factor.

Here we take the bypass configuration with only one bus waveguide for simplicity. We assume the electric field amplitudes of

| + l ?

(CW) and

| ? l ?

(CCW) modes are

a_{1}

and

a_{2}

, respectively. The resonance frequency is

ω_{0}

. The time-independent coupling coefficients

κ_{12}

and

κ_{21}

can be computed by the electric field overlapping between two modes, which is

κ_{kl} = ω_{0} / 2 \int d r^{3} Δ ?_{I} E_{k}^{*} (r) E_{l} (r)

. In a single-mode waveguide, the spatial mode profile across the cross section is the same for

| \pm l ?

. Thus, we can reduce the coupling coefficient expression to

κ_{12} = κ_{21} = κ_{m} = ω_{0} Δ ?_{I} / 4 ?

[34]. Here

?

is the permittivity of the medium without modulation.

Incorporating the excitation from the bus waveguide, the coupled mode equations are

\frac{d a_{1}}{d t} = (? i ω_{0} ? \frac{1}{τ}) a_{1} + i κ_{m} e^{? i ω_{m} t} a_{2} + μ_{1} s_{+ 1},

(E1)

\frac{d a_{2}}{d t} = (? i ω_{0} ? \frac{1}{τ}) a_{2} + i κ_{m} e^{i ω_{m} t} a_{2} + μ_{2} s_{+ 2} .

(E2)

Here

s_{+ 1}

and

s_{+ 2}

are field amplitudes of excitation from port 1 and port 2.

ω_{m}

is the modulation frequency.

μ_{1} = μ_{2} = μ

are evanescent coupling coefficients between the bus waveguide and

| \pm l ?

modes.

1 / τ

is the total loss factor including coupling, scattering, and radiation loss.

The output field transmission coefficient from port 1 (

s_{? 1}

) and port 2 (

s_{? 2}

) can be expressed as

s_{? 1} = e^{i ?_{1}} (s_{+ 1} ? μ_{1}^{*} a_{1}),

(E3)

s_{? 2} = e^{i ?_{2}} (s_{+ 2} ? μ_{2}^{*} a_{2}),

(E4)

where

?_{1}

and

?_{2}

are coupling phases. With all the equations above, the normalized transmission spectra with excitation from different ports are solved as

T_{21} (ω) = {| \frac{s_{? 2}}{s_{+ 1}} |}^{2} = {| 1 + \frac{i (ω_{s} ? ω_{m}) {| μ |}^{2}}{(ω_{m} ? ω_{s}) ω_{s} + κ_{m}^{2}} |}^{2},

(E5)

T_{12} (ω) = {| \frac{s_{? 1}}{s_{+ 2}} |}^{2} = {| 1 + \frac{i (ω_{s} + ω_{m}) {| μ |}^{2}}{? (ω_{m} + ω_{s}) ω_{s} + κ_{m}^{2}} |}^{2},

(E6)

where

ω_{s} = ω ? ω_{0} ? 1 / i τ

indicates the complex resonance frequency. The calculated curves based on coupled mode theory fit the simulation result well in broken APT phase as depicted in Fig.?8. The resonances are shifted oppositely with excitation from different ports. Considering the existence of temporal modulation, this system is indeed nonreciprocal in broken APT phase.

Figure 8.Transmission spectra

T_{21}

and

T_{12}

around resonance

| \pm 18 ⟩

in broken APT phase. The micro-ring diameter is smaller than the one in the main text. The crosses are simulation results under three different

Δ ϵ

, and the curves are theoretical calculation from Eqs. (E5) and (E6). Here

Δ ϵ_{th}

is the modulation depth at EP.

The single-mode APT symmetry lasing mechanism can be further explained by temporal field evolution inside a micro-ring cavity. Interference patterns of

| \pm 17 ?

excited by a pulse around 1550?nm in broken APT phase are shown in Figs.?9(a)–9(c). The intensity profile is not azimuthally uniform along the ring and decays gradually. Within one modulation period

1 / ω_{m}

, the movement of intensity maxima is not synchronized with the motion of the modulation profile. The field maxima travel across both gain and loss regions without any preference of staying in one region compared with the other. Adding the inherent loss of the system, the time-averaged energy dissipation rate will be lossy, and the field intensity is observed to decay gradually. As a comparison, the field movement in unbroken APT phase is synchronized with the evolution of modulation, as depicted in Figs.?9(d)–9(f). The field localized in the gain region will be consistently amplified and finally contribute to the lasing in the micro-ring. It is worth mentioning that this works only when the number of field maxima exactly equals the period of modulation along the micro-ring. Any deviation from this equality will reduce overlapping between the gain region and field intensity, leading to a larger lasing threshold. With reasonable pumping intensity, the lasing can be controlled within a single mode without any disturbance from other longitudinal modes, which explains what we observe in Fig.?4(d).

Figure 9.Intensity distribution at different times in (a)–(c) broken APT phase and (d)–(f) unbroken APT phase for

| \pm 17 ⟩

. The modulation propagates counterclockwise with frequency of

ω_{m} = 1 THz

. (a), (d) Intensity profile at

t = t_{0}

; (b), (e) at

t = t_{0} + t_{m} / 3

; (c), (f) at

t = t_{0} + 2 t_{m} / 3

. Here

t_{0}

t_{m}

are reference time and the period of spatiotemporal modulation (

t_{m} = 1 / ω_{m}

), respectively. Insets show zoom-in view of the interference patterns and modulation profile in the blue dashed box. The red and yellow arrows indicate the traveling directions of both modulation and intensity profiles, respectively. The black arrow and black dashed lines mark the full width at half maximum of the intensity profile.